不考虑空气阻力时候,二者无论是同体积还是同同重量,到达地面时候速度相同。
而最终坑的大小在于球对地面释放的能量多少。
分析接触地面时候,球体会发生弹性形变,这个形变会提供一个向上的力,在一个是地面的阻力,我们把这两个力合称为向上阻力吧。还有与周围土壤接触时候的摩擦力(这个摩擦力对于另外两种力来说很小,忽略掉)。
显然向上阻力与接触面积有关(接触面大的话,弹性形变提供的力就大)。
则相同体积情况下,土壤材质相同提供的阻力相同,则坑的大小取决于球的硬度,则木头显然比铁软,则铁球砸的坑大。
相同质量情况下,一方面,木球体积变大,接触面变大,另一方面,木头比铁软,二者都会导致坑变小,则忽略阻力情况下,铁球坑大(很符合生活常识)。
考虑空气阻力,我们分析最终速度。(假设到达地面时候重力依然大于阻力)
首先考虑阻力公式。

c为阻力系数,ρ为空气密度,S为接触面积,v为相对空气的速度。其中cρ都是常数,且对于一个已知的物体,显然S也是一个常数,为了方便,我们记此公式为
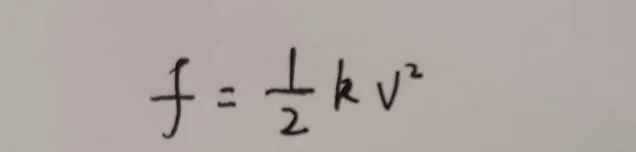
则可列出运动方程

然而这个微分方程并不好解,我们换另一种思路,借助动量定理的微分形式,即dp=Fdt,即dp/dt=F,可以得出

接下来,我们来分析这个解。
首先,可以知道v与t,k都有关,根据常识,有了阻力最终速度一定会比无阻力要小,我们设二者之差为Δv。
而另一方面,k增大会导致物体运动时间延长,我们设这个时间差为Δt,则由动量定理,mg(t₀+Δt)-阻力冲量=mv,其中v为最终速度。而无阻力时,mgt₀=mv₀,v₀为无阻力的最终速度,那么可知,mgΔt-阻力冲量=mΔv,可见最终Δv的大小与Δt,k有关,Δt与k又有关,最终我们还是要回到对k对t的关系上。
由已知的速度,可得出

我们得到了t关于k的函数式,这里面由于我们关心的始终是最终的时间大小与最终的速度大小,那么我们就先把x当做一个常数。这个式子看着非常复杂,如果严谨来做的话,那么就要把v看成k,t的复合函数,其中t=t(k),之后在求出v关于k的偏导数=∂v/∂k+∂v/∂t·∂t/∂k,这会非常复杂。那我们能否定性的去分析呢?
我是这样考虑的(不知道对不对)

可以看到t近似与k½成正比。那么带入到v的表达式(这里其实是最终速度的大小),求其关于k的导数,得到

那么我们可以看出,最终的v还与m,k的关系有关。对于同重量不同密度的球,二者S不同,这种情况结果会非常复杂,因为最终还需要考虑接触面积导致的弹性力的变化问题。但当S相同时,k相同了就如二者最终会归为最开始讨论的无阻力问题。










