跑车跑一圈圆形跑道或一般曲线跑道的最短耗时
1、抗倾覆条件
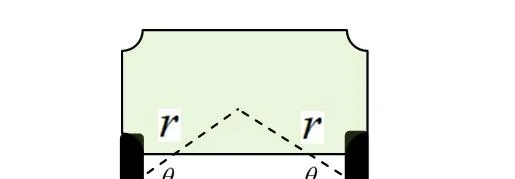
惯性离心力引起的倾覆力矩应不超过跑车自身的抗倾覆力矩。记跑车重量 mg ,重心位置如图示,那么应有:
mgr\cos\theta\geq m\frac{v^2}{R}r\sin\theta
由此解得: v\leq\sqrt{gR\cot\theta}\qquad(1)
2、抗滑移条件
惯性离心力不应超过地面提供的最大摩擦力,故:
\mu mg\geq m\frac{v^2}{R}
因此: v\leq\sqrt{\mu gR}\qquad(2)
综合式(1)和式(2),得到跑车的理论最大速度:
v_{max}=\sqrt{\min(\cot\theta,\mu)gR}:=\sqrt{\xi gR}
刚才看到知友 @ace zh 提供的相当专业的道路设计资料,实际道路的弯道设计还可能存在一个刻意的外侧加高。假设外侧加高可以等价为一个道路的初始小倾角 \theta_{0} ,籍此容易得到抗倾覆条件为:
v\leq\sqrt{gR\cot(\theta-\theta_{0})}\qquad(3)
抗滑移条件为:
v\leq\sqrt{ \frac{\mu+\tan\theta_{0}}{1-\mu\tan\theta_{0}}gR}\qquad(4)
易见小倾角 \theta_{0} 的效果,既相当于降低了跑车底盘,也相当于增大了道路摩擦系数,最终提高了跑车的理论最大速度。此时 \xi 系数可以一般地表为:
\xi =\min \left( \frac{\mu+\tan\theta_{0}}{1-\mu\tan\theta_{0}},\cot(\theta-\theta_{0})\right)
3、跑一圈所用的理论最短时间
T_{min}=\int_{0}^{2\pi R}\frac{ds}{v_{max}}=2\pi\sqrt{\frac{R}{\xi g}}
4、举例
假设某圆形跑道每圈10公里,即取 2\pi R=10\;km; R\approx1.592\; km; 不设外侧加高。 轮胎在沥青马路上的摩擦系数通常可取0.6,假设跑车重心足够低,那么 \xi=0.6 ,于是有:
T_{min}=\sqrt{\frac{2\pi\times10000 }{0.6\times9.8}}\approx103.37\;(s)\approx1.72\;(min)
极限时速: v_{max}=\sqrt{\xi gR}=\sqrt{0.6\times9.8\times1592}\approx350\;(km/h)
也就是说,不管跑车的动力多么强劲,它跑一圈这种10 km 跑道,速度不可能超过350 km/h。
5、一般光滑曲线围成的跑道
令跑道的参数方程:
x=x(t);y=y(t);\quad(t_{1}\leq t \leq t_{2})
容易计算曲率:
\kappa=\frac{1}{R}=\frac{\ddot{y}\dot{x}-\dot{y}\ddot{x}}{(\dot{x}^2+\dot{y}^2)^{3/2}}
微弧长:
ds=\sqrt{\dot{x}^2+\dot{y}^2}dt
跑一圈的理论最短时间:
T_{min}=\int_{t_{1}}^{t_{2}}\frac{ds}{\sqrt{\xi gR}}=\int_{t_{1}}^{t_{2}}\sqrt{\frac{\ddot{y}\dot{x}-\dot{y}\ddot{x}}{\xi g(\dot{x}^2+\dot{y}^2)^{1/2}}}dt
值得指出,这个最短时间公式也适用于存在零曲率段的跑道。直观起见,举一个椭圆跑道的例子,令跑道方程:
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\rightarrow x=a\cos t;y=b\sin t\;(0\leq t \lt 2\pi)
则跑一圈椭圆轨道的理论最短时间:
T_{min}=\int_{t_{1}}^{t_{2}}\sqrt{\frac{\ddot{y}\dot{x}-\dot{y}\ddot{x}}{\xi g(\dot{x}^2+\dot{y}^2)^{1/2}}}dt
=\sqrt{\frac{ab}{\xi g}}\int_{0}^{2\pi}{\frac{dt}{(a^2\sin^2t+b^2\cos^2t)^{1/4}}}
6、结语
以上讨论未考虑跑车自身动力限制(最大速度)以及空气阻力因素,这些因素考虑进去, T_{min} 当然还会有所增大。











