袁講經典18:以一道變速圓周運動題目為例講兩個知識點
真的好久沒有更新了,最近在探索做影片直播,失敗了!
我們繼續文字分享吧!
例1: 如下圖所示,在豎直平面內,輕繩a和輕繩b懸掛一質素為 m 的小球處於靜止狀態,其中輕繩a為水平,輕繩b與豎直方向角度為 \theta ,現在剪斷輕繩a的瞬間,求輕繩b的拉力大小和小球的加速度大小。
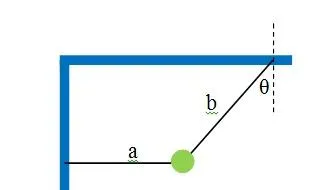
解: 這道題是一道變速圓周運動問題,那麽變速圓周運動又有哪些公式可以用呢?
我們看一下勻速圓周運動的公式,如下,
F_n=m\frac{v^2}{r}=m\omega^2 r=m(\frac{2π}{T})^2r ,
那麽這個公式在變速圓周運動中是否還可以使用呢?
首先, F_n=m(\frac{2π}{T})^2r 肯定不能用了,因為周期是個平均概念,變速圓周運動中速度、角速度時刻在變化,所以該公式無法使用,
而 F_n=m\frac{v^2}{r}=m\omega^2 r 公式依然可以使用, 但是使用時要註意:
1.要采用瞬時速度大小和瞬時角速度大小,瞬時速度和瞬時角速度之間的關系依然滿足 v=\omega r ,但我們高中一般很少用到瞬時角速度,所以一般采用 F_n=m\frac{v^2}{r} 公式。
2.註意該公式中的 F_n 並不是合力,只是指向圓心方向(法向)的力,至於切向方向的力也依然滿足牛頓第二定律,
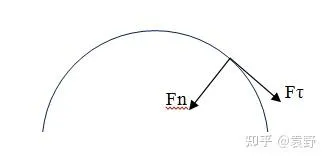
如上滿足,
F_n=ma_n=m\frac{v^2}{r} , F_τ=ma_τ ,
其中 a_n 和 a_τ 分別稱為法向加速度和切向加速度,
那麽合加速度為, a=\sqrt{a_n^2+a_τ^2} 。
好了,我們回到上面這道題目,剪斷輕繩a的瞬間受力分析如下,
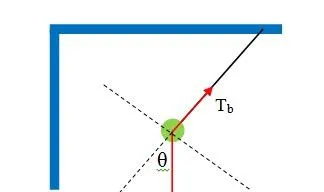
因為接下來小球是做變速圓周運動,所以我們要在法向和切向進行力的分解,
法向, T_b-mg\cos\theta=ma_n=m\frac{v^2}{r} ,其中剪斷瞬間 v=0 ,
切向, mg\sin\theta=ma_τ ,
解得, T_b=mg\cos\theta , a_n=0 , a_\tau=g\sin\theta ,
所以, a=\sqrt{a_n^2+a_τ^2}=a_\tau=g\sin\theta ,
即,輕繩b的拉力大小為 T_b=mg\cos\theta ,小球的加速度大小為 a=g\sin\theta 。
好了,做完了,這就是關於變速圓周運動題目的做法。
下面留一個問題,第一個留言且回答正確的小夥伴們私信作者獲取10元購書券一張(僅可用於購買袁野老師的物理輔導書)
例2: 上題中,現在剪斷輕繩b的瞬間,求輕繩a的拉力大小和小球的加速度大小。
好了,小夥伴們抓緊留言吧。
我們接著往下說,在上題中,在還沒有剪斷輕繩前,我們計算兩根輕繩的拉力大小,特別簡單吧,得到, T_{a0}=mg\tan\theta , T_{b0}=\frac{mg}{\cos\theta} ,
然後我們對比 T_{b0} 和 T_b 發現,繩子的拉力存在突變。
但是我們在做上面這道題目的時候, 根本不關心剪斷前繩子的拉力大小!
這就是關於繩子瞬態問題的解法,叫做,
繩子看後!
但如果是彈簧,就不一樣了。叫做,
彈簧看前!
為什麽呢?
繩子和彈簧的拉力都是因為發生彈性形變產生的,但繩子的彈性形變肉眼不可見,易突變,彈簧的彈性形變肉眼可見,很大,恢復需要時間!
好了,然後,我們將上題改編為,
例3: 如下圖所示,在豎直平面內,輕彈簧a和輕彈簧b懸掛一質素為 m 的小球處於靜止狀態,其中輕彈簧a為水平,輕彈簧b於豎直方向角度為 \theta ,現在剪斷輕彈簧a的瞬間,求輕彈簧b的拉力大小和小球的加速度大小。
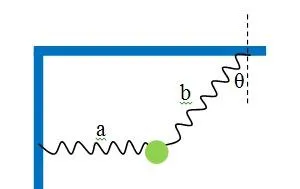
解: 首先說一說輕彈簧a的情況,因為剪斷了,所以不用考慮了,
當然很多小夥伴對這個都有疑問,認為剪斷的瞬間不是還保持拉長的形變麽,怎麽就不考慮了呢,
因為我也沒有說明在哪裏剪斷,你可以認為在靠近小球的附近剪斷不就可以了嗎!當然這樣想比較牽強,而本質是因為輕彈簧的「輕」,「輕」就是不考慮質素,就是沒有質素,沒有質素的物體在高中物理中必須受力平衡,否則根據牛頓第二定律將產生無窮大的加速度,也就是說輕彈簧不存在一端受力的情況,即輕彈簧不存在如下受力情況,
這就是模型限制,沒必要深究,如果非要說現實中是可以這樣一端受力的呀,那現實中彈簧有質素的呀,如果告訴你彈簧質素,或特許以算一算。
好了,現在我們就當做剪斷的彈簧就沒啥用了。
那麽這道題目怎麽做呢?
記住彈簧看前!
所以,我們計算沒有剪斷前兩彈簧的彈力大小分別為,
T_{a0}=mg\tan\theta , T_{b0}=\frac{mg}{\cos\theta} ,
剪斷瞬間, T_{a}=0 , T_{b}=T_{b0}=\frac{mg}{\cos\theta} ,
所以此時,彈簧b的拉力大小不變,重力不變,所以,
\vec {mg}+\vec {T_{b}}=-\vec{T_{a0}} (向量計算)
也就得到此時小球的加速度大小為, a=\frac{T_{a0}}{m}=g\tan\theta ,
好了,這樣就做完了,我們根本不關心剪斷後小球做什麽運動,事實上我們也很難分析剪斷後小球復雜的曲線運動是什麽樣的。
好了,今天這道題目,我們至少學到了兩點:
1.變速圓周運動向心力公式怎麽用!
2.瞬態問題,繩子看後,彈簧看前!
小夥伴們,咱們下期再見啦!










