這裏用盡量淺顯的語言來表達這樣一個結論:
熱力學中的吉布士熵就是資訊熵在熱力學系統中的特定套用: 它是我們在已知某個熱力學系統宏觀狀態的前提下,對系統微觀資訊的無知量 。
我們可以先從資訊熵說起。
資訊熵
舉個例子,比如說你在考試的時候,遇到一道判斷題,一道單選題,還有一道多選題。這三道題你都完全不會。這時候,你有機會偷窺其中一道題的答案,那麽,你會選擇偷窺哪一道題呢?
這是一個非常簡單的選擇,我們會選擇多選題。但是為啥呢?
因為多選題最「難猜」。
一道判斷題有兩個可能答案,正確或錯誤。因此我們猜一個答案就有50%的概率可以蒙對。而一道單選題則有A、B、C、D四種可能答案,那麽我們猜一個就有25%的概率蒙對。那麽一道多選題呢,他有如下種可能答案:
A、B、C、D、AB、AC、AD、BC、BD、CD、ABC、ABD、BCD、ACD、ABCD
一個好的出題者會盡量讓自己的題目達到最難猜的程度,也就是說,上述所有可能答案的概率都一樣。也就是說,我們猜一個答案就只有1/15的概率蒙對。
也就是說,如果有人告訴我們答案,我們獲得的資訊量肯定是多選題>單選題>判斷題。
這個例子告訴我們, 我們對一個問題的無知程度,取決於這個問題中可能選項的概率 。如果每個選項的概率都很低,那麽我們就很難猜對答案,我們就對這個問題很無知。如果其中某一個選項的概率非常高,那麽我們就有很大的自信去選擇這個選項。於我們就對這個問題有相當的確定性。
消除我們更多的無知,就需要更多的資訊;反之,如果只是消除一點點無知,則只需要一點點資訊。於是這種資訊量就是:
I\sim -f\left( p_i \right)
此外,如果我們有兩個問題。告訴我們第一個問題的答案,我們就獲得了 I_1 的資訊量,告訴我們第二個問題的答案,我們就獲得了 I_2 的資訊量。那麽把兩個問題的答案全告訴我們,顯然我們就獲得了 I_1+I_2 的資訊量。但是,從概率的角度,兩個問題的正確概率卻是每個問題的概率的乘積,也就是說:
I=-f\left( p_1p_2 \right)=I_1+I_2=-f\left( p_1 \right)-f\left( p_2 \right)
上述公式成立,就要求 f 是一個對數類別的函數。也就是說,資訊量是由概率的對數來描述的。
對於一個特定的問題,它有若幹種可能,每一種可能都對應著一個概率。那麽,它的答案的資訊量我們就可以取 所有這些可能選項的概率的對數的期望值 ,也就是:
S_S=-\sum_{i}{p_i\lg p_i}
這個就是資訊熵。下標s這裏表示是山農熵,以和後面的吉布士熵做區分。
我們回到上面的例子,對一個判斷題來說,有兩種可能性,那麽很容易算出來,其資訊熵就是1位元。這很容易理解,因為我們只用0和1兩個數碼來編碼對和錯,就可以告訴我們答案了。對一個單選題來說,就是兩個位元。也就是說,我們用這樣的編碼,00:A、01:B、10:C、11:D,就可以告訴我們答案了。而多選題,就是3.9個位元。因為我們用4個位元可以編碼16種選擇,但是這裏只有15種選擇,也就是說4位元略有冗余。
那麽,資訊熵和熱力學熵又有何關聯呢?
吉布士熵
我們來看一個熱力學系統。對這個系統的狀態,我們應該如何描述呢?我們有兩種方法。
第一種就是從微觀角度來精確描述系統中的每一個分子的狀態:這些分子的動量和位置。如果每一個分子的狀態都被描述清楚了,那麽整個系統的狀態也就描述清楚了。這叫做 微觀態(microstate) 。典型的熱力學系統中大約有1mol的分子,每個分子有6個狀態量:三個方向上的位置座標和三個方向上的動量。那麽典型的熱力學系統的微觀自由度就有 6\times 6\times10^{23} 個。也就是說,如果我們精確知道了這麽多變量的數值,我們就得到了系統的全部資訊。
在現實中,我們顯然不可能知道系統的微觀狀態:這需要太多變量了。比如說,我們用一個單精度浮點數(32位元)來記錄其中每一個變量,這種精度已經是很低的了。那麽1mol最簡單的單分子理想氣體(比如說氦氣),就需要我們用10YB的儲存空間。據統計,2021年全球的總儲存量大約是470EB。 [2] 也就是說,這個資訊量是現在全球總儲存能力的3萬倍。
所以,在實際上,我們用第二種方法來描述熱力學系統,就是從宏觀角度。用幾個變量來描述系統的整體,只看它在宏觀上的表現,諸如溫度、壓力、密度、組成等等。這樣一來,我們就忽略了它的每一個分子的具體運動狀態。這種描述下的系統狀態就叫做 宏觀態(macrostate) 。一般而言,對一個系統,宏觀態的自由度只有幾個。這個自由度可以透過吉布士相律來計算:
F=C-P+2
其中,C是系統的組分數,P是系統中包含的相態數。對於單組份單相系統(比如說一箱氦氣),它的自由度就只有兩個。大家常用溫度和壓力來描述這個狀態(當然,也可以用諸如能量、熵、焓、自由能等狀態函數)。
也就是說,熱力學上, 我們對系統的描述就忽略了大量的微觀資訊 。
現在我們來問,已知一個宏觀態,我們想要知道它的精確微觀狀態,我們需要多少資訊量呢?
我們說,對已知的宏觀態,有無數種可能的微觀態。我們把這些可能的微觀態出現的概率記作 p_i 。那麽它的資訊熵就是:
S_S=-\sum_{i}{p_i\lg p_i}
這就是吉布士熵。事實上,吉布士熵和資訊熵在表述形式上有一點不同,科學家喜歡自然對數,而計算科學家們喜歡以2為底的對數。然後在補上一個波茲曼常數:
S_G=-k_B\sum_{i}{p_i\ln p_i}
這就是 吉布士熵 。(這裏我們考慮離散情況,對於連續的情況,就把上述公式裏的概率變成概率密度,把加和變成一個積分)
我們可以這麽來看待吉布士熵: 我們用簡單的宏觀自由度描述大量微觀自由度的時候,所損失掉的資訊量再乘以一個系數。
我們再來看看熵增原理。
熵增和混沌
從上面的討論我們可以知道, 當所有的各種可能性出現的概率都相等的時候,我們對一個問題的無知度最高。 這一點很容易理解,當你面對一個選擇題的時候,如果你知道B選項的概率高於其他選項,你對這道題的把握肯定會高於所有選項概率都相等的情況。
這恰恰就是平衡態。
也就是說, 平衡態有最大的熵,意味著平衡態是我們對系統最無知的一種狀態。而系統總是向著熵增的方向演化,就意味著我們不斷遺失系統的資訊。
這一點我們可以進一步挖掘。
如果從系統的某個初態演化,如果我們透過微觀動力學預測它未來的熵變,我們會發現整個過程中 熵守恒 ,而不是 熵增 。(這裏說的是經典動力學,量子力學其實本質上和這個區別並不大,但這是另外一個故事了。)
也就是說,如果我們嚴格遵守底層規律,我們從初態知道多少資訊,在未來就總會是無失真的。這個其實很自然:因為從微觀動力學看,一個保守系統其實是資訊守恒的(動力學是完全決定論的,也即是如果知道一個初態,我們會準確預測它的未來)。
但是,這個看起來就和熱力學第二定律出現矛盾了。問題出在哪裏呢?
歷史上,波茲曼的一個統計力學基本假設就是 分子混沌假說(Stosszahlansatz) 。這個假說說的是,分子碰撞的速度之間是不相關聯的。這顯然是違背基本動力學原理的,因為它們都是來自動力學方程式,顯然不可能做到不相關聯。在那個時候,混沌理論尚未建立。但是恰恰是這個未來才出現的混沌理論,為這個矛盾提供了一種解釋。
混沌理論預言了兩個關鍵動力學特征: 一個是演化對初始條件極端敏感;另一個是相空間的碎形結構。 第一個特征意味著,相空間種的相體積會被不斷拉伸,第二個特征意味著,演化過程中初始的相體積會變成任意精細的結構。這裏我用一個簡單的碎形系統做一個直觀的演示。
如下圖,我們用一個簡單的二維空間來表示一個熱力學系統全部的可能微觀狀態空間(相空間)。某一個熱力學系統在初始時刻從某個初始狀態出發開始演化。我們對初始狀態做出一個觀察,由於觀察精度所限,我們不可能得到一個精確狀態,而只能得到一個可能的範圍:藍色的區域就是這個系統在初始時刻的可能初始狀態範圍(系綜)。
隨著系統演化,我們透過動力學方程式計算這個區域的狀態隨時間的變化情況。它會在狀態空間中發生形變。前面說了,這個範圍會不斷拉伸(初始條件敏感)。同時由於系統的非線性特征,它還會發生彎折、扭曲等一系列形變。由於資訊的守恒,這個 範圍所覆蓋的面積卻不會發生變化 。下面就是一種非常簡單的演化方式:它只涉及了拉伸和彎曲兩種形變,這個形變過程就形成了一種叫做 「龍之曲線」 的碎形結構(影片用python寫成)。
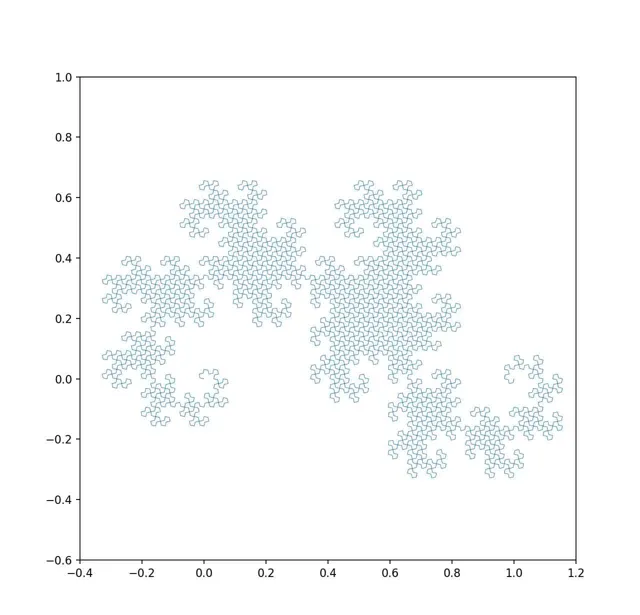 「龍之曲線」的演化歷史
https://www.zhihu.com/video/1449765365841006592
「龍之曲線」的演化歷史
https://www.zhihu.com/video/1449765365841006592
我們可以看到,系統從一個初始的小範圍可能性(小面積)最終變成了一個大範圍可能性(大面積)的過程。
但是,我們的演化規則卻是,這個範圍所覆蓋的面積不發生變化。這裏的關鍵就在於,隨著演化的過程,初始的面積被越拉越長,變成了一條細線。隨著不斷拉伸,這條線越來越細。但是我們的觀察精度卻不允許我們 辨識 無線精細的線形,所以到了一定程度後,我們所觀察的線形就不再繼續變細了 - 雖然「實際上」它在變細,但是我們卻無法觀察了。最終,這個範圍的演化越來越精細,看上去就成了一個範圍更大的面積。這個,吉布士把它叫做「 粗粒化 」。也就是說,在相空間中,我們無法辨識足夠精細的結構,而只能把這個相空間分成有限體積的「像素」看待。透過這種變化, 我們就在一定的精度之外,遺失了系統的進一步演化資訊。
這種碎形結構,是混沌理論的一個預言。關於碎形,這裏就不多說了,請參考
的確,如果我們可以不斷提高我們的觀察精度,我們的確可以看到足夠精細的結構,從而「還原」出它的細線本質(影片由python寫成):
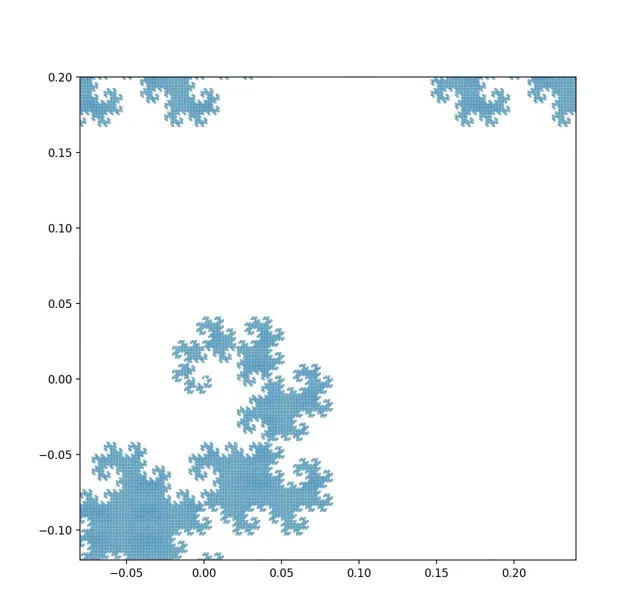 揭示龍之曲線的精細結構
https://www.zhihu.com/video/1449768887402942464
揭示龍之曲線的精細結構
https://www.zhihu.com/video/1449768887402942464
但是,統計力學本身就是一個粗粒化的學科。如果我們不需要粗粒化,也就不需要統計力學了。
當然,這種粗粒化的解釋、吉布士熵和波茲曼熵以及熱力學熵(克勞修斯熵)之間的關系、乃至系綜方法本身,現在也都存在著諸多的爭議。這就是另外的故事了,本文不涉及。我計劃在未來為我的專欄裏寫的文章裏加以覆蓋。這是一個已經停更兩年的專欄了,最近計劃拾起來繼續更新,這裏先做一個廣告:
前面我們從統計力學的角度,大概講了一下系統演化過程中的資訊遺失過程,進而把熵增歸結於資訊的遺失。那麽從熱力學的角度,我們如何把資訊和熵聯系在一起呢?
資訊熵和熱力學熵
我們可以這麽來說,從熱力學角度, 一個系統的熵表征著它內部「廢能量」的多少 。所謂的「廢能量」指的是在現有的熱力學條件下無法用來對外做功的能量。
也就是說,熵越大,系統對外做功的能力越小。熵越小,系統對外做功的能力越大。如果聯系到我們上面所說的資訊熵和熱力學熵的關系,這句話可以直觀地理解為: 我們對系統了解越多,則我們可能利用系統對外做的功就越多。
這句話其實挺好理解,也挺容易想象的。
比如說,我們有一個水庫,水庫看起來很平靜。如果我們比較粗糙地觀察它,我們認為它處在平衡態,是一個熵最大的狀態,因此我們無法用它來做功。
但是如果我們在水庫中放置多個傳感器,我們就會發現在表面的平靜狀態下,它內部其實暗流湧動。很顯然,從熱力學可以計算,有暗流的水體有著比平衡態的水體更低的熵:這和我們前面的論述相一致,因為我們對水體的監控更加細致,也就有著更多關於水體的資訊了。
假如說我們手中有一個引擎,並且透過某種操作可以把它放置在水中任意一個地方。於是我們就可以透過我們對暗流的監控,隨時把這個引擎放在暗流最大的地方。透過這種暗流就可以推動引擎做功。也就是說,這時候我們發現水庫就有了對外做功的能力了。
我們對水庫的監控越精細,我們對它的資訊就了解得越多,因而我們對水體所觀察的熵值就越低,而此時我們操控引擎做功的能力就越大。
聰明如你,你應該立刻意識到,這個引擎的操作員其實就是一個粗糙版的麥克斯韋妖。只不過我們把麥妖放在了一個相對宏觀的情形下了。
問題是,我們本身都是宏觀的物體,因此我們在這種有宏觀效應的漲落中,就可以透過獲取更多的資訊來做功。在微觀世界裏,情況就很復雜,比如說著名的Szilard引擎。 [3] 這裏涉及到一個資訊的處理和讀寫的極限的問題。也就是著名的 「麥妖驅魔」(Exorcism of Maxwell Demon) 問題。 [4] 當然,這就是另外一個故事了。
參考
- ^ doi.org/10.1119/1.1971557
- ^https://www.statista.com/statistics/638593/worldwide-data-center-storage-capacity-cloud-vs-traditional/
- ^https://en.wikipedia.org/wiki/Entropy_in_thermodynamics_and_information_theory#Szilard's_engine
- ^https://en.wikipedia.org/wiki/Maxwell's_demon











