Plateau's problem(
普拉托問題)
這個問題看上去非常簡單,就是問在邊界固定的情況下,什麽樣子的曲面面積最小。這在物理上是一個很顯然的問題。根據
普拉托定律,你拿個鐵絲彎成邊界,然後吹肥皂泡就好了。但是這個在數學上來說,是一門學科,幾何測度論(
Geometric measure theory)的核心問題。
為什麽說這個問題難呢?我們考慮一個簡單的情形,即在三維空間中邊界為圓弧的曲面。這個問題答案很顯然,就是圓盤。但是從數學角度而言,這個不簡單。
通常的想法就是,我們可以把曲面視為一個從二維圓盤到三維空間的對映,然後利用變分法去考慮這個問題。但是這個方法有著很多毛病,其中最大的問題就是缺乏緊性。我們不妨試著跟著這個思路走一下,看看會出怎樣的問題。
1. 遍歷所有可能的曲面,然後取一個面積趨近於最小(infimum)的序列;
2. 找出一個收斂子序列;
3. 證明極限就是我們想要的曲面,即最小曲面。
在這三步計劃中,第二步就會出現很大的問題。比如:
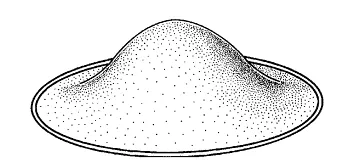
【我是一個有理想的曲面,我的目標是要成為極小曲面】
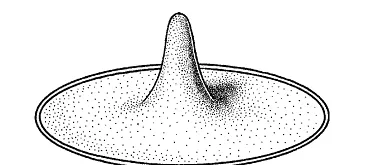
【嗯,我的面積縮小了。感覺好棒!】
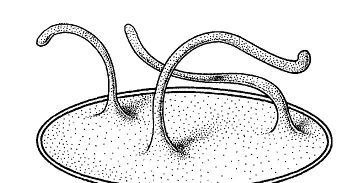
【我的面積又縮小了。可是為什麽我感覺怪怪的呢……】

【啊……肯定有……有什麽不對……啊……怎麽回事……我的面積明明縮小了啊……為什麽……我感覺好奇怪啊……不行啊……為什麽會變得這麽奇怪呢……啊……】
【圖片來源:Geometric Measure Theory: A Beginner's Guide 作者:Frank Morgan】
【請紳士們嚴肅看待這些圖片,不要想歪了!也不要「我好興奮啊」 ! 】
換句話說,即使是曲面的面積在趨近於\pi ,你所取得序列也可能長得非常奇怪,有很多很多的觸手(馬猴燒酒的好朋友),甚至於這些觸手可以觸及空間中所有的有理點。換句話說,你最後得到的東西的閉包是整個\mathbb R^3 .
看看,物理中多麽顯然的東西,在數學中就是這麽的讓人糾結。存在性就已經夠難了,更別說正則性(即最小曲面是否光滑等等)……這個問題直到20世紀中期才有解決方法。具體方法涉及專業知識較多,我自己也不是很熟悉,就不細說了。
其實這種問題很多。比如在給定條件(比如邊值)下的拉普拉斯方程式
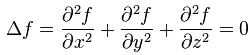
的解的問題。這個問題在物理上也是幾乎顯然的,因為電勢就是解。但是在數學上這個問題並不簡單,一般而言需要Sobolev空間等知識進行解決。
【其實我真的不是來黑物理的2333333333 表打我(╯^╰)】
==============2015年5月6日10:31:54(馬德裏時間)============
那些說我黑數學的人你們夠了。請你們仔細思考一下:普拉托定律僅僅是經驗性定律,根本無法保證在所有的情況下結論都成立。而數學就是將特殊到一般的過程。
另外,下面的回答中已經有人補充了,數學上關於曲面面積的定義。在上面第二步中,我說找到一族收斂子序列,其實是很不嚴謹的。因為我沒有說是什麽收斂,也沒有說收斂極限在哪兒。事實上我們需要的極限必須是可求面積的曲面(請跟可求長度的曲線比較起來理解)。所以如何保證極限不會很奇怪,就是存在性的主要工作。











