第一次回答一個跟自己的專業相關的題目。
首先,為什麽要進行變換?因為很多時候,頻率域比時域直觀得多。
傅立葉級數和傅立葉變換,表明時域的訊號可以分解為不同頻率的正弦波的疊加。而如果我們把兩個沒有公共頻率成分的訊號相加,一同發送。在接收端接收到之後,用濾波器把兩個訊號分開,就可以還原出發送的兩個訊號。這就是通訊過程的實質。
而在這個過程中,發送端發送出去的訊號的最大頻率和最小頻率是否在接收端的帶通濾波器的上下邊界頻率之內?如果超出了濾波器的頻率範圍,接收端接收到的訊號就會遺失一部份資訊,接收端接收到的訊息就會有錯誤。
但這個問題從時域是很難看出來的,不過,從頻率域就一目了然。
因此傅立葉變換得到了廣泛套用,它的地位也非常重要。
然而,可以進行傅立葉變換的訊號似乎不那麽夠用,傅立葉變換的收斂有一個狄利克雷條件,要求訊號絕對可積/絕對可和。
為了使不滿足這一條件的訊號,也能讀出它的「頻率」,拉普拉斯變換和Z變換,對「頻率」的含義做出了擴充,使得大多數有用訊號都具有了對應的「頻率」域運算式,方便了對各個器件的設計。
這裏, 我們並不是透過拉氏變換和Z變換獲取不滿足狄利克雷條件的函數的傅氏變換 。事實上由於收斂域的問題,這些函數的傅氏變換是不收斂的, 即使透過拉氏變換和Z變換也不可能獲得這些函數的傅氏變換。
拉氏變換和Z變換的意義,是將頻率域的某些限制條件A,轉化為復頻率域中與之等價的相應條件A',然後在復頻域內直接觀察訊號或系統的 拉氏變換或Z變換 ,看X(s)或X(z)是否滿足條件A',得到相應的結論。用這個結論代替傅立葉變換的結論(因為傅立葉變換不存在,無法得出結論)。
=====================================
接下來一個問題,傅氏變換、拉氏變換、Z變換之間到底有什麽關系?
首先,傅立葉變換粗略分來包括連續時間傅立葉變換(CTFT)、離散時間傅立葉變換(DTFT)。
CTFT是將連續時間訊號變換到頻域,將頻率的含義擴充之後,就得到拉普拉斯變換。
DTFT是將離散時間訊號變換到頻域,將頻率的含義擴充之後,就得到Z變換。
但事實上我們在繪制頻譜圖的時候,取的自變量都是 \omega ,這樣才能畫出函數影像。否則CTFT和DTFT都將變成複數平面上變化的函數,無法畫出函數影像了。
而且我們日常用到頻率這一概念時所說的 f ,都是 f=\frac{\omega}{2\pi} .其對應的角頻率恰恰是實數 \omega ,而不是復數 j\omega 或 e^{j\omega} 。
因此,我們所說的頻率指的應當是 \omega 而不是 j\omega 或 e^{j\omega} 。
1、連續時間傅立葉變換與拉普拉斯變換的關系
連續時間傅立葉變換的公式是:\int_{-\infty}^{\infty } x(t)e^{-j\omega t} dt
,這裏的\omega
是實數。
傅立葉變換要求時域訊號絕對可積,即\int_{-\infty }^{\infty } \left| x(t) \right| dt<\infty
。
為了讓不符合這個條件的訊號,也能變換到頻率域,我們給x(t)乘上一個指數函數e^{-\sigma t}
,\sigma
為(滿足收斂域的)任意實數。
可以發現,x(t)e^{-\sigma t}
這個函數,就滿足了絕對可積的條件,即\int_{-\infty }^{\infty } \left| x(t)e^{-\sigma t} \right| dt<\infty
。
用更加嚴謹的數學表達,對於大多數 x(t) , \exists \sigma\in \Re ,使得\lim_{t \rightarrow \infty}{e^{-\sigma t}} 是 \lim_{t \rightarrow \infty}{x\left( t \right)} 的高階無窮小。即 \lim_{t \rightarrow \infty}{\frac{e^{-\sigma t}}{x\left( t \right)}}=0 。因此在 e^{-\sigma t} 的壓迫下, x(t)e^{-\sigma t} 就滿足了絕對可積的條件。後文DTFT中的絕對可和條件與此類似,後文不再贅述。
於是這個新函數的傅立葉變換就是:\int_{-\infty }^{\infty } x(t)e^{-\sigma t} e^{-j\omega t} dt
,
化簡得\int_{-\infty }^{\infty } x(t)e^{-(\sigma +j\omega )t}
。
顯然\sigma +j\omega
是一個復數,我們把這個復數定義為一個新的變量——復頻率,記為s。
於是便得到了拉普拉斯變換的公式:\int_{-\infty }^{\infty } x(t)e^{-st} dt
拉普拉斯變換解決了不滿足絕對可積條件的連續訊號,變換到頻率域的問題,同時也對「頻率」的定義進行了擴充。
所以拉普拉斯變換與連續時間傅立葉變換的關系是:
拉普拉斯變換將頻率從實數推廣為復數,因而傅立葉變換變成了拉普拉斯變換的一個特例。
當s為純虛數時,x(t)的拉普拉斯變換,即為x(t)的傅立葉變換。
從影像的角度來說,拉普拉斯變換得到的頻譜是一個複數平面上的函數,(為方便作圖,這裏只給出了拉氏變換的振幅譜和傅氏變換的振幅譜的關系。相位譜具有類似的關系。)
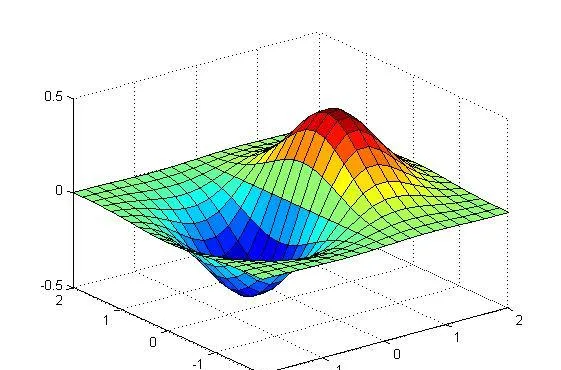
而傅立葉變換得到的頻譜,則是從虛軸上切一刀,得到的函數的剖面。
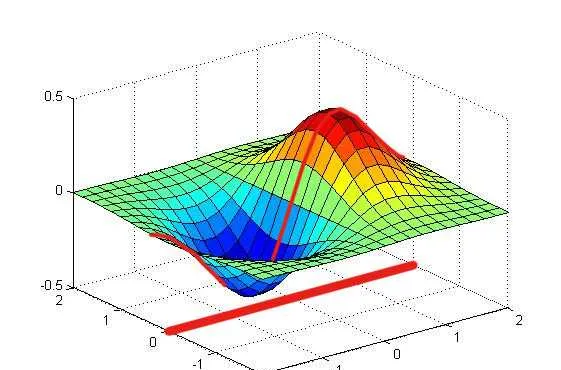
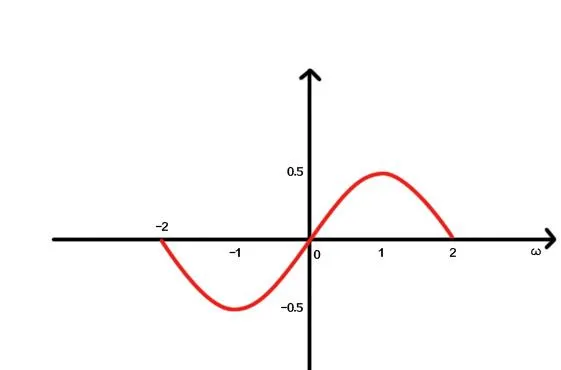
2、離散時間傅立葉變換(DTFT)與Z變換的關系
DTFT的公式是\sum_{n=-\infty }^{\infty }{x[n]e^{-j\omega n} }
,這裏的\omega
是連續變化的實數。
同樣的,DTFT需要滿足絕對可和的條件,即\sum_{n=-\infty }^{\infty }{\left| x[n] \right| } <\infty
。
為了讓不滿足絕對可和條件的函數x[n],也能變換到頻率域,我們乘一個指數函數a^{-n}
,a
為(滿足收斂域的)任意實數。
則函數x[n]a^{-n}
的DTFT為:\sum_{n=-\infty }^{\infty }{x[n]a^{-n}e^{-j\omega n} }
,
化簡得:\sum_{n=-\infty }^{\infty }{x[n](a\cdot e^{j\omega })^{-n} }
顯然,a\cdot e^{j\omega }
是一個極座標形式的復數,我們把這個復數定義為離散訊號的復頻率,記為z。
則得到Z變換的公式:\sum_{n=-\infty }^{\infty }{x[n]z^{-n} }
。
而Z變換令 z=a\cdot e^{j\omega} ,則當a=1,即 z=e^{j\omega} 時,隨著 \omega 從 -\infty 向 +\infty 變化,z在複數平面中的單位圓上以 2\pi 為周期變化,如此恰能充分利用DTFT的周期性進一步簡化我們的計算。
Z變換解決了不滿足絕對可和條件的離散訊號,變換到頻率域的問題,同時也同樣對「頻率」的定義進行了擴充。
所以Z變換與離散時間傅立葉變換(DTFT)的關系是:
Z變換將頻率從實數推廣為復數,因而DTFT變成了Z變換的一個特例。
當z的模為1時,x[n]的Z變換即為x[n]的DTFT。
從影像的角度來說,Z變換得到的頻譜,是一個複數平面上的函數,而DTFT得到的頻譜,則是沿著單位圓切一刀,得到的函數的剖面,從負實數軸切斷展開的影像。(為方便作圖,這裏只給出了Z變換的振幅譜和傅氏變換的振幅譜的關系。相位譜具有類似的關系。)
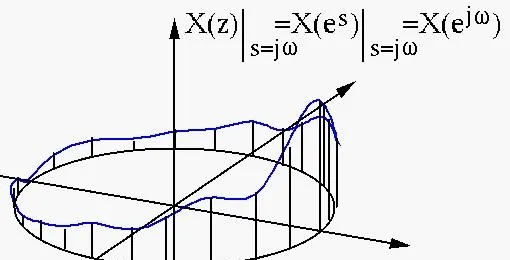
感謝評論區 @蔡世勛提供的圖片。











