更新修正一些你們沒發現的bug,並且指出悖論的解決核心:
四加速的分量在兩個參考系都是相等的. (這太顯然了所以我繞一大圈算給你看)
----------
取光速c=1 , 假設發射速度是v . 帶撇的是實驗系的變量,不帶撇是運動系的變量.
認為電子發射的方向是z, 兩個電子連線是x方向,右手座標系, 只考慮發射後的瞬間 , 以其中一個電子為原點,則電子參考系的電磁場如下:
\begin{aligned} \vec{E}&=-\frac{e}{4\pi\epsilon_0}\left(\frac{\vec{r}}{r^3}+\frac{\vec{l}+\vec{r}}{|\vec{l}+\vec{r}|^3}\right)\\ \vec{B}&=0\\ \end{aligned}
如果只考慮 該電子受到的電磁場 :
\begin{aligned} \vec{E}&=-\frac{e}{4\pi\epsilon_0}\frac{\vec{l}+\vec{r}}{|\vec{l}+\vec{r}|^3}\\ \vec{B}&=0\\ \end{aligned}
(電子能不能感受到自己的庫倫作用,這個問題到量子場論裏面再解決)
那麽電磁場張量就是:
F_{\mu\nu}= \begin{pmatrix} 0&E_x&E_y&E_z\\ -E_x&0&-B_z&B_y\\ -E_y&B_z&0&-B_x\\ -E_z&-B_y&B_x&0\\ \end{pmatrix} =-\frac{e}{4\pi\epsilon_0}\cdot\frac{1}{|\vec{l}+\vec{r}|^3} \begin{pmatrix} 0&x+l_x&y+l_y&z+l_z\\ -x-l_x&0&0&0\\ -y-l_y&0&0&0\\ -z-l_z&0&0&0\\ \end{pmatrix}
利用勞侖茲變換 (p.s. v 前面的負號來自對協變指標變換):
\Lambda^\alpha_\beta= \begin{pmatrix} \gamma&&&-\gamma v\\ &1&&\\ &&1&\\ -\gamma v&&&\gamma\\ \end{pmatrix} ,其中\gamma=\frac{1}{\sqrt{1-v^2}} ,
則實驗系中的電磁場張量:
\begin{aligned} F'_{\mu\nu}=\Lambda^T F\Lambda &= \begin{pmatrix} 0&E'_x&E'_y&E'_z\\ -E'_x&0&-B'_z&B'_y\\ -E'_y&B'_z&0&-B'_x\\ -E'_z&-B'_y&B'_x&0\\ \end{pmatrix}\\ &= \begin{pmatrix} 0&\gamma(E_x+vB_y)&\gamma(E_y-vB_x)&E_z\\ -\gamma(E_x+vB_y)&0&-B_z&\gamma(B_y+vE_x)\\ -\gamma(E_y-vB_x)&B_z&0&-\gamma(B_x-vE_x)\\ -E_z&-\gamma(B_y+vE_x)&\gamma(B_x-vE_x)&0\\ \end{pmatrix}\\ &= \begin{pmatrix} 0&\gamma E_x&\gamma E_y& E_z\\ -\gamma E_x&0&0&v\gamma E_x\\ -\gamma E_y&0&0&v\gamma E_y\\ - E_z&-v \gamma E_x&-v \gamma E_y&0\\ \end{pmatrix}\\ &=-\frac{e}{4\pi\epsilon_0}\cdot\frac{\gamma}{|\vec{l}+\vec{r}|^3} \begin{pmatrix} 0&x+l_x&y+l_y&(z+l_z)/\gamma\\ -x-l_x&0&0&v(x+l_x)\\ -y-l_y&0&0&v(y+l_y)\\ -(z+l_z)/\gamma&-v(x+l_x)&-v(y+l_y)&0\\ \end{pmatrix}\\ \end{aligned}
也就是說, 在 這個瞬間 ,實驗室系,另一個電子對這個電子作用的電磁場是:
\begin{aligned} \vec{E}'&=(\gamma E_x,\gamma E_y, E_z)=-\frac{e}{4\pi\epsilon_0}\cdot\frac{\gamma}{|\vec{l}+\vec{r}|^3}\left(x+l_x,y+l_y,(z+l_z)/\gamma\right)\\ \vec{B}'&=(-v\gamma E_y,v\gamma E_x,0 ) =-\frac{e}{4\pi\epsilon_0}\cdot\frac{v\gamma}{|\vec{l}+\vec{r}|^3}\left(-y-l_y,x+l_x,0\right) \\ \end{aligned}
所以代入:
\begin{aligned} \vec{r}&=(x,y,z)=0\\ \vec{l}&=(l,0,0)\\ \vec{v}&=(0,0,v)\\ \end{aligned}
算得 此瞬間 電磁作用的力:
\vec{F}=-e(\vec{E}+\vec{v}\times\vec{B})=\left(\frac{e^2\gamma}{4\pi\epsilon_0l^2},0,0\right)+\left(-\frac{e^2\gamma v^2}{4\pi\epsilon_0l^2},0,0\right)=\left(\sqrt{1-v^2}\frac{e^2}{4\pi\epsilon_0l^2},0,0\right)
即 庫倫相互作用乘上一個因子 \sqrt{1-v^2} . 就是
@白如冰的結果.
這個結論無論要怎麽解讀都好,畢竟數學的結論就擺在這裏。
不過等會我會證明\sqrt{1-v^2} 可以被理解為時間膨脹效應\sqrt{1-v^2}=\frac{\mathrm{d}t'}{\mathrm{d}t}
重要:
(1)
包括我在其他人評論下提到的,力的勞侖茲變換其實是很tricky的一個東西, 力的話一定要有一個測力計之類的東西來測量的,而測力計顯視器上的數碼總是一個"勞侖茲不變量", 代表的是測力計那個參考系的結論。
而在高能物理中,庫倫作用是透過虛光子來傳遞的,「力」已經不是一個好的物理量,因為測力計彈簧的彈性也是庫倫作用決定的.
盡管如此,在理論物理中,你可以透過動量的變化定義不一樣的"力",它們都有"力"的因次:
\frac{\mathrm{d}p}{\mathrm{d}t}\,\,\,,\,\,\,\frac{\mathrm{d}p}{\mathrm{d}t'}\,\,\,,\,\,\,\frac{\mathrm{d}p'}{\mathrm{d}t}\,\,\,,\,\,\,\frac{\mathrm{d}p'}{\mathrm{d}t'}
其中 帶撇的是實驗系的變量,不帶撇是運動系的變量 , 即便它們在低速下的空間分量都回到牛頓力學的定義\vec{F}=\frac{\mathrm{d}\vec{p'}}{\mathrm{d}t'} ,然而這裏 具有勞侖茲協變性的「力」 只有f=\frac{\mathrm{d}p'}{\mathrm{d}t}=\frac{\mathrm{d}p'}{\mathrm{d}\tau}
稱為4-force,t\to\tau 是記號習慣,稱為原時, 是勞侖茲不變量.
並且,我們上面算的F=q(E+v\times B) 並不是 4-force.
真正 協變的 4-force是 f_\mu=qF_{\mu\nu}u^\nu , 用人話講就是:
\begin{aligned} f^0&=q\gamma\vec{E}\cdot\vec{v}\\ f^i&=q\gamma(\vec{E}+\vec{v}\times\vec{B}), \,\,\,i=1,2,3 \end{aligned}
4-force除以靜止質素就是4-acceleration(4-加速度a_\mu=f_\mu/m_0 ), 是另一個協變的向量.
比較有意思的:
4-force的空間分量, 剛好就是庫倫相互作用的大小 :
f^i=\left(\frac{e^2}{4\pi\epsilon_0 l^2},0,0\right)
因為boost的方向和電場力的方向正交,所以不受影響,這只是個偶然的結果。 這也恰恰說明,四加速度的x 分量在兩個參考系是一樣的.
所以「悖論」在這裏就解決了.
回到我們剛才的計算結果,\vec{f}=\frac{\mathrm{d}\vec{p'}}{\mathrm{d}t}=\frac{\mathrm{d}\vec{p'}}{\mathrm{d}t'}\frac{\mathrm{d}t'}{\mathrm{d}t}=\frac{\mathrm{d}\vec{p'}}{\mathrm{d}t'}\sqrt{1-v^2}=\vec{F}\sqrt{1-v^2} . 於是我們證明了這個因子可以認為完全是時間膨脹帶來的,如果扣除了這個因子,那麽兩個「力」是一樣的. 不過我認為四加速已經是最簡潔的方法了,你可以以此換算成其他的量.
(2)
這是墜重要的,直接和高中知識點聯系的:
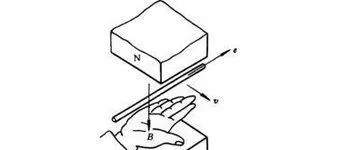
我們都知道切割磁感線產生的 動生電動勢並不能直接從麥克斯韋方程式組中得到 ,然而這在狹義相對論中是顯而易見的:(感謝
@辛坤毓指正,原為感生電動勢)
如圖,實驗室系中我們有:
F'= \begin{pmatrix} 0&0&0&0\\ 0&0&0&B'_y\\ 0&0&0&0\\ 0&-B'_y&0&0\\ \end{pmatrix}
那麽導線系中,我們有:
\begin{aligned} F=(\Lambda^{-1})^TF\Lambda^{-1} &= \begin{pmatrix} 0&E_x&E_y&E_z\\ -E_x&0&-B_z&B_y\\ -E_y&B_z&0&-B_x\\ -E_z&-B_y&B_x&0\\ \end{pmatrix} \\ &= \begin{pmatrix} 0&-\gamma vB'_y&0&0\\ \gamma vB'_y&0&0&-\gamma B'_y\\ 0&0&0&0\\ 0&\gamma B'_y&0&0\\ \end{pmatrix} \end{aligned}
所以在導線的參考系中有x方向的電場:E_x=-\gamma vB'_y\approx -vB_y'
即和速度(約)成正比的動生電動勢\mathcal{E}=E\Delta l=vB\Delta L , 符合「右手定則」
所以愛因斯坦的狹義相對論論文叫做【 論動體的電動力學 】











