並不是這個專業的,但是說一下我的看法吧
1/3到2/3這個指的是中學實驗課上用的那種,機械式的電流表,不是現在的數碼式表。而這個1/3到2/3指的也是一個大概區域,不是精確範圍。
這是因為這種電流表的原理是依靠一個彈簧的扭力和安培力二力矩平衡,用測量安培力來測量電流
測量原理很簡單,安培力: F=BIL ,彈簧扭力 F=k\theta ,顯然,只需要二力的力臂比例就能從旋轉角度 \theta 測出來電流I,而且二者是線性的。
但是,這一切都是理論。因為在實際上存在兩個額外的變量:
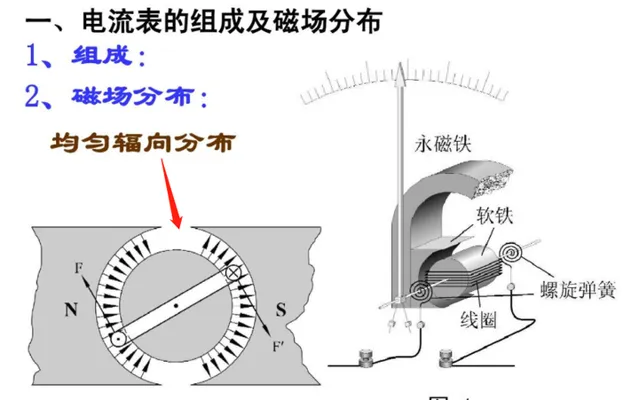
安培力中重要的磁感應強度B不是不變的,因磁場不是均勻輻向分布,而是在兩端存在磁感線的不均勻分布。所以只有角度轉到中間這段的時候B才接近是不變的。所以 中間區間線性度最好 。
其次,扭力的轉動彈性模量k也不是一個常數,這是材料學上的事情,虎克定律只是一個近似定律,是把分子間作用勢近似為二次函數的結果。
這樣就導致一個結果,就是實際上電流I和角度θ之間的關系是一個近似線性但是又不是線性的關系。從數學上,我們可以用一個泰勒(麥克勞林)近似來表達:
I=k_1\theta+k_2\theta^2+k_3\theta^3 ... \tag1
但實際情況是電流表又是一個刻度均勻的表,所以我們需要用一個線性函數來表示,即:
我們需要用一個線性函數 I=k\theta +\theta_0 來最大限度的擬合(1)。
我們隨便選一個接近線性的非線性函數做一下這個擬合,就知道結果了兩端處誤差太大......
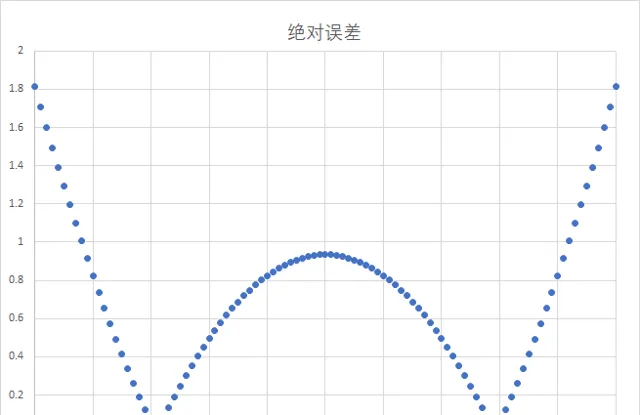
而實際上還有一個因素,那就是中間段線性最好,所以肯定選中間校表......這樣的話擬合實際上是取中間段做擬合然後外推到整個量程的。
如果我們線性擬合(校表)取x在30~70之間那誤差結果就會變成這樣:
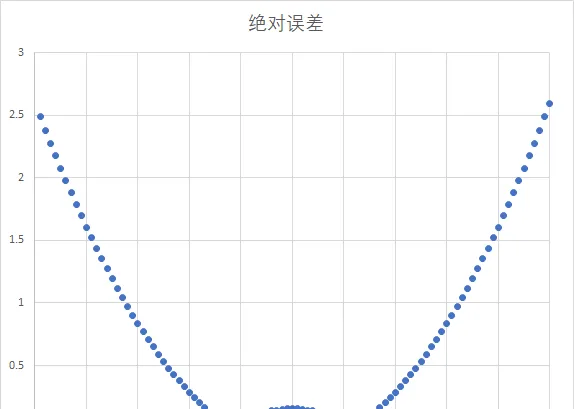
看到了嗎,此時才是一個校準後的電流表的誤差狀況,中間最靠譜,而兩側最不靠譜。
另外,數碼式不一定適用這個規則。因為數碼式的最大好處就是可以直接用非線性擬合來輸出結果,所以數碼式下這個規律就不一定對了。











