謝邀。拋塊兒磚。
首先回答「除了美觀還有什麽作用」。
地圖既是一種工具也是一種藝術。地圖輪廓以及填充、標註的簡化(cartographic generalization,感謝 任暢同學的糾正,官方中文轉譯叫制圖綜合)的主要目的,其實已經被題主說到了:準確、簡潔、美觀。其實還有一個目的,那就是透過減少細節來 突出重點 。
當畫幅(比例尺)變化的時候,很多的細節不可能都一一地表現在圖上。例如下圖(來自加拿大的拉瓦爾大學):
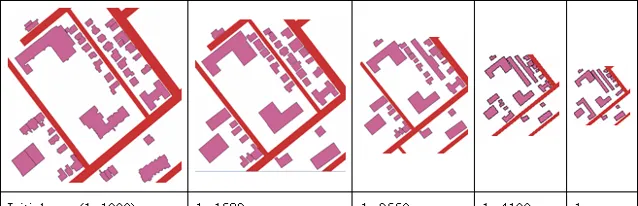
比例尺是1:1000的時候,地圖上可以保留很多細節,比如所有的路徑,以及各個建築的輪廓。但是到了1:27176的時候,如果再保留所有路徑或建築的輪廓,那就一團亂麻,什麽也看不清了。
有時候,少也是多(Less is more)。只有削去了不重要的枝枝葉葉,主幹的資訊才能更好地被突出展現出來,地圖才能達到它應有的效果。
而且,比例尺並不是地圖簡化的唯一原因。每一幅地圖都有自己的目的。目的不一樣,對於各種細節的要求也就不一樣。比如網上這張反映一帶一路的地圖:
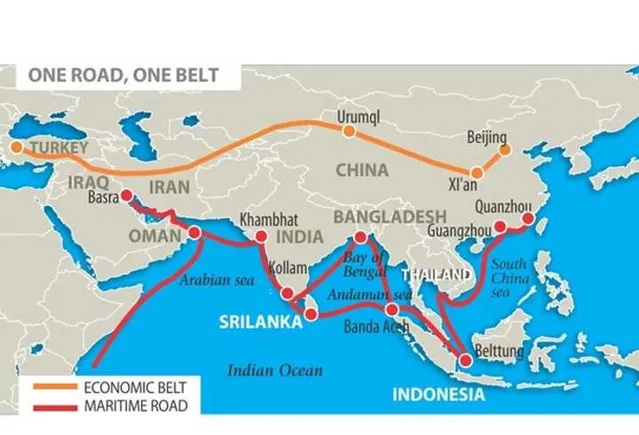
經常看地圖冊的人一眼就能看出很多「錯誤」,比如北京的位置貌似偏了些,瓊州海峽沒了,馬爾代夫和琉球也沒了,日本那幾個島也連在一起了,等等。但是,這張圖的目的是展現一帶一路,並不是為了告訴人們馬爾代夫在哪裏,北京在哪裏。弱化了一些細枝末節的東西,則更能強調出一帶一路的這個主題。試想一下,如果這張地圖把陸地輪廓畫得特別詳細,還加上中國的省界,甚至長江黃河,那它的主題會不會反而被沖淡了?
接下來就具體回答題主最主要的一個問題:地圖的細節是怎樣被簡化掉的?
從種類上說,map generalization可以分為:

題主在題目補充裏談的是海岸線的簡化,也就是地圖的線性輪廓(海岸線、國界線、河流、等高線……)的簡化,即上面談到的方式裏的Simplified。
繪制輪廓一般用的是向量數據。所以,這裏討論的地圖輪廓簡化方法,實際上也是向量數據的壓縮方法。
介紹具體方法以前,先要說一下總體的前提條件。不管多復雜的曲線,我們也認為它是由一個個的線段組成的,而線段的兩端都是一個個的數據點。越「圓滑」的輪廓,數據點就越多。
常見的簡化方法有這幾種:
1. 簡單粗暴 - 隔點法
隔點法就是在向量曲線的一系列點中,每隔n個點選取一個來保留,其余沒選中的點都刪除。比如說下面這張圖的曲線:
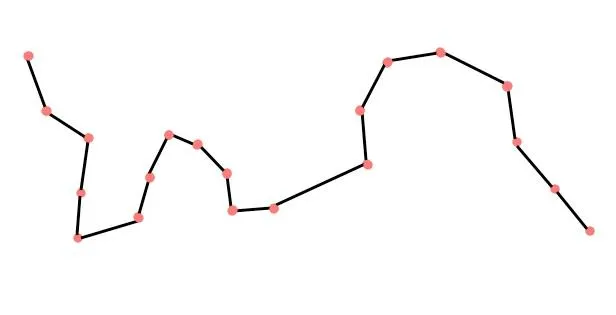
現在我每隔2個點選擇一個留下,剩下的點刪除,就把這條曲線簡化成了紫色的這種樣子:
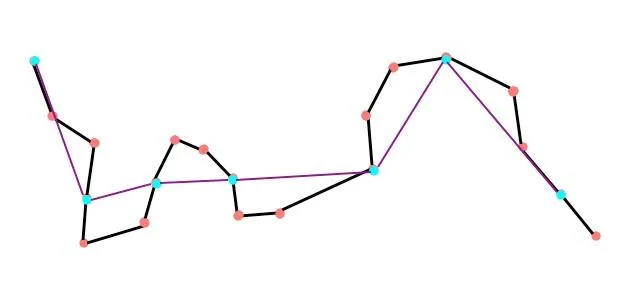
如果我每隔3個點選擇一個留下,則簡化後的曲線是這個樣子的:
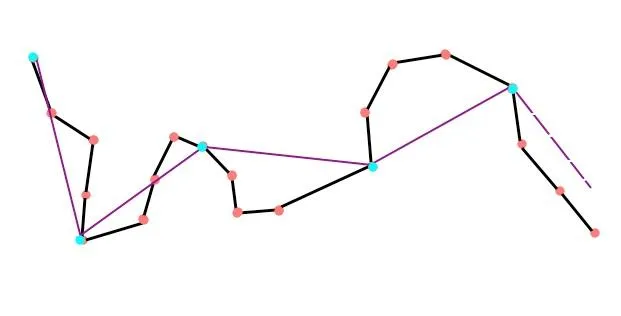
這種做法的優點是演算法簡單,操作簡單,但是缺點是比較重要、有特色的點很可能會被漏掉。在原本的曲線就不那麽平滑的情況下,這麽做很可能造成比較大的形變。比如地圖上的半島或者海灣,在n選擇不當的時候,很可能就直接被切掉了。
2. 步步為營 - 垂距法
這種垂距法是一種比較常用的辦法。它是按照某個指定的方向,一步一步地簡化曲線。比如下面這張圖:
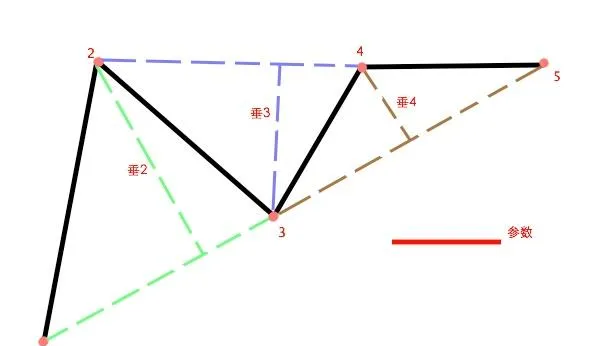
首先我們要指定一個參數長度,比如圖中的紅色線段。
然後,我決定從左到右地簡化這條曲線,因此我首先要選擇1、2、3這三個點。
連線1和3,然後透過2作垂線和1、3的連線相交。測量垂2的長度。圖中,垂2的長度大於參數,因此要保留點2.
然後挪位到2、3、4這三個點,連線2和4,再畫出垂3。比較垂3和參數。這裏的垂3還是大於參數,因此點3也保留。
然後挪位到3、4、5這三個點。連線3和5,再作垂4.這裏,垂4的長度是小於參數的,因此點4就要被刪除掉。
然後繼續向右,挪位到3、5、6(4被刪除了)等等一直進行下去。
3. 宏觀調控 - 分裂法
這種方法還有一種高大上的名字叫做道格拉斯·皮尤克演算法,也是一種用得比較多的方法。它和垂距法有相似之處,都是需要設定一個參量來進行比較。但是它們也有很大的不同。比如,垂距法是從左到右(或者從右打左)一步一步地進行曲線簡化。而道格拉斯·皮尤克演算法則是把整個曲線看做一個整體,來進行「宏觀調控」。它的具體操作如下。
比如,現在有這麽條曲線:
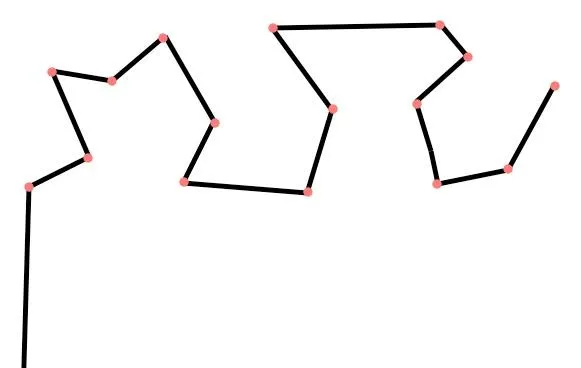
用這種方法,我們就要從整體入手:
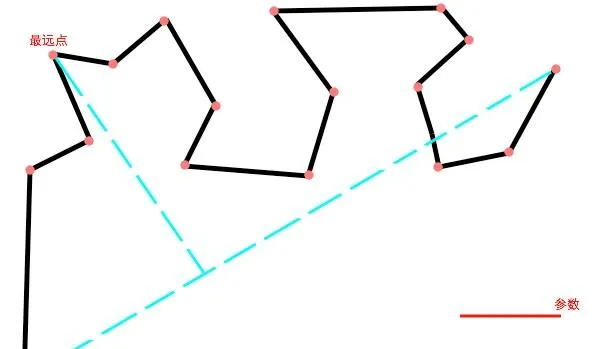
首先要做的就是選參數「紅色線段」。然後連線整條曲線的首位兩點。連線之後,找出離這條連線距離最遠的那個點,比較這個點到連線的距離和所選參數的大小。圖中現在的最遠點是明顯大於參數的,因此這個點被保留。
然後進行下一步:
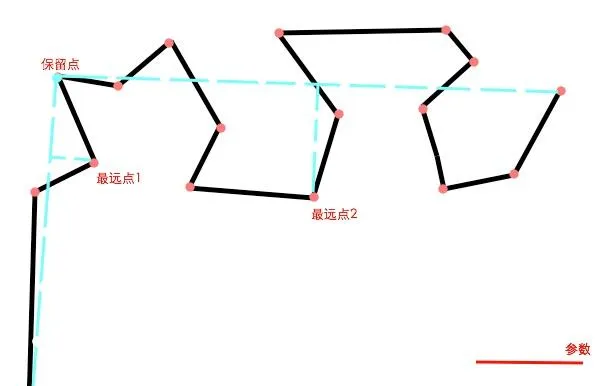
連線起始點和保留點,以及終點和保留點。再分別找出兩條連線區間範圍內的最遠點,並將它們的距離和參數比較。這裏,最遠點1的距離是小於參數的,因此在這個區間內的所有點都要被刪除掉。而最遠點2的距離剛好大於參數,因此最遠點2也成為了被選取的保留點。
接下來:
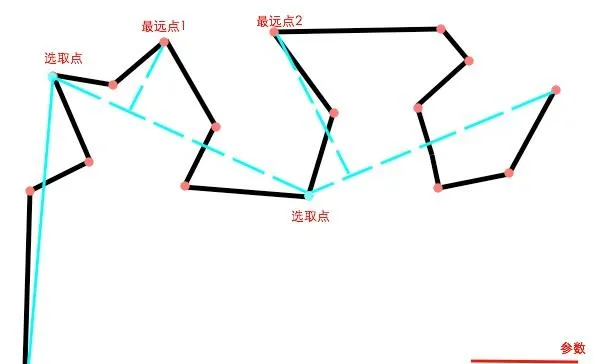
連線上一個保留點和新的保留點,以及新的保留點和終點,同樣的道理,分別找出兩個區間內的最遠點以及距離。這裏的最遠點1的距離小於參數,因此這一區間的所有點都刪除。最遠點2的距離大於參數,則成為新的選取點被保留。
同理繼續進行篩選:
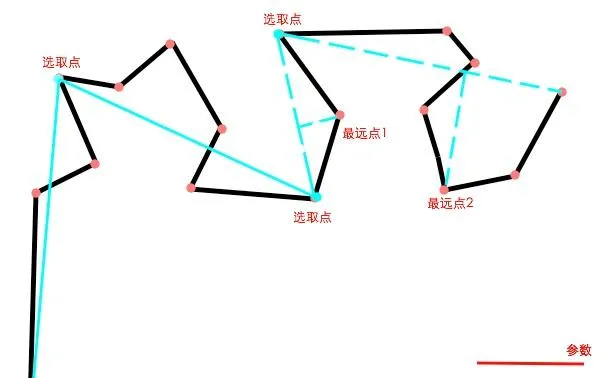
最遠點1所在區間的點被刪除,最遠點2成為新的選取點被保留。
再來一次:

這次最遠點1保留,最遠點2所在區間的點刪除。
再來一次:
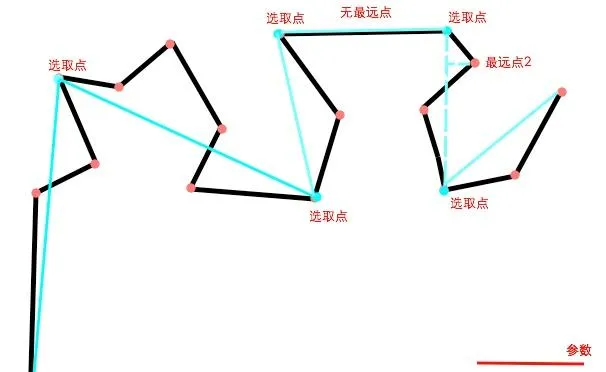
同樣的作法。
最後,這條藍色的曲線就是透過道格拉斯·皮尤克演算法簡化後的曲線:
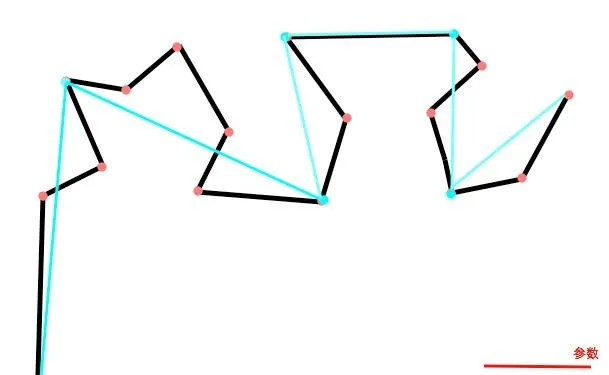
不論是垂距法還是道格拉斯·皮尤克演算法,重要的一點都是要選擇一個合適的參數。參數越大,地圖被簡化的程度就越大。
知乎專欄:地球的那些事兒











