如果你是一個漫畫家
你要在雜誌上開始新連載了!
這可真是個好訊息,對吧?
但是別急,還有個壞訊息,那就是你的讀者非常挑剔。
哪種挑剔?
就是說他們見不得哪怕一點點相同!
姑且舉個反面例子好了,讓我們看看下面這個四格漫畫。
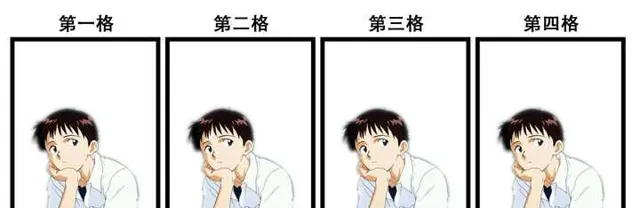
作為一個漫畫——如果它可以被這麽稱呼的話——實在是太糟糕了。
第一格到第四格,都只畫了同一個人,擺著同一個姿勢。
雖然這個角色確實很南通,但是你不能弄得如此堂而皇之。
你不能把讀者當傻子糊弄。
好吧,給我回爐重造,重新畫一個。
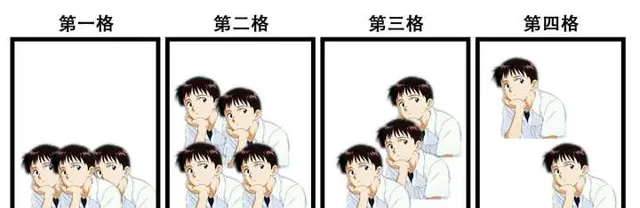
…………………………
畫的什麽JB?不是說你把人數給我整多就行。
好家夥,還有的格子裏錯落有致,有的格子裏整整齊齊,突出一個難以捉摸。
你擱這養蠱呢,還是擱這套娃呢?

我必須提醒你,故事需要逐步展開。
因此,你必須按照以下規則來畫:
第一格裏只能畫1個人,第二格裏最多2個人,第三格裏最多3個人。
如此一來,才不會出現第一格裏的角色就多到讀者記不住的地步。
好吧,再畫!

好好好,這麽玩是吧。
等差數列算是被你小子學明白了。
這b玩意要是能在周刊上連載,除非全世界讀者的頭都被驢踢了。
能不能畫點陽間的漫畫?

說實話,我逐漸開始懷疑,你是不是只會畫這個男的?
別忘了,我們的讀者非常厭惡相同。
讓我把話說得更直白通俗一點:
你不能畫出任何和此前的分鏡完全一樣的格子,這是最基本的職業素養。
甚至,如果去掉任意個角色後,和此前的某一格完全一樣,這也是不被允許的。
因為這意味著你把之前的分鏡復制貼上二次利用了。

希望你能夠明白一件事,那就是:
如果你只會畫這個男的,那你將只能按照雜誌的要求畫出一格漫畫。
多一格都畫不出來了。
TREE(1)=1
所以,你必須學會畫另一個角色!
來吧,請允許我向各位介紹我的老婆:

現在,我們有了兩個角色:
真嗣和麗。
我們再來試試,按照雜誌社的要求能畫出幾格漫畫。
不賣關子了,直接說吧,我們將能夠畫出3格分鏡,卻無論如何畫不出第4格。

為什麽是這樣?
因為第一格裏只能畫一個真嗣,從此以後,真嗣就不能再出現了,否則去掉真嗣以外的所有人物後,必定和真嗣重復。
值得一提的是,第二格必須畫兩個麗。如果只畫一個,你將會發現第三格無人可畫。

看來想要多畫幾格分鏡實屬不易啊。
但是不論如何,我們從TREE(1)=1,突破到了TREE(2)=3,這絕對是個偉大的進步。
這進步來源於哪裏?
沒錯,來源於老婆。
因此如果我們想要打破桎梏,仍然需要老婆的幫助。
先生們,請掌聲歡迎我的小老婆。

真不錯,老婆的數量開始……不是,你會畫的角色開始多了起來。
那麽,該是時候告訴你我們的最後一條規矩了。
我們的讀者要求很嚴格,他們要你每一個分鏡裏,必須有一個「 夏娃角色 」。
夏娃角色是這格分鏡故事的起點,所有後續角色都由她發出的線條來連線。
因此夏娃角色就像是祖先,會「生下」子孫,而祖先和子孫們合起來仍然必須滿足我們上面提過的兩條規則:
①第一格只能畫1個角色,第二格不超過2個角色,第三格不超過3個角色……
②去掉任意角色後,不能和此前畫過的格子完全一樣。
讓我給你舉個例子好了。
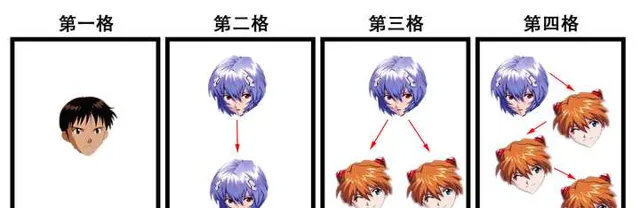
就像大樹的根支撐著幹,幹又長出樹枝一樣。
每個角色向上去尋根溯源,一定能找到最初的「夏娃角色」。
夏娃,也就是EVA,是一格分鏡裏所有角色的祖先。
當然了,很多時候不需要追溯到夏娃,就能找到共同的長輩。
比如你和你的表妹,有同一個外祖母。
知道了這一點,你就可以聽一下我們漫畫的最後一條規定:
③任意兩個相同角色在不同分鏡裏,最近的共同祖先不能相同
聽起來有點繞對吧?看看下面這個圖
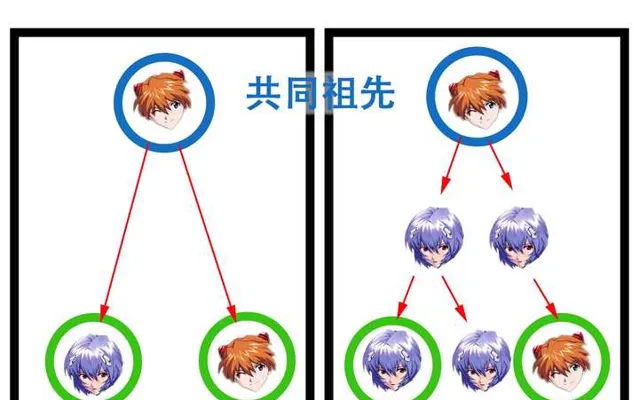
綜上所述,我們有三條限制,來規定你分鏡的繪畫方式。
當你只會畫真嗣的時候,你只能畫1格漫畫,便被迫停刊。
當你會畫真嗣和麗的時候,你能畫3格漫畫,同樣就無從下筆了。
那麽,現在你會畫真嗣、麗和香香三個角色,你覺得自己能連載多少格?
直覺上估計,感覺沒多少對吧?
1→3→X,按這個規律X能到100都頂天了。
然而實際上,在不違背規則的情況下,你能畫出的格子數目,遠遠超過了這個宇宙的基本粒子數。
這個格子的數目,就是大名鼎鼎的TREE(3)。
我用黑色表示真嗣,藍色表示麗,橘色表示香香,簡單展示一下TREE(3)前12個可行的分鏡。
同樣的,真嗣只能在第一格露個臉,此後就沒他什麽事了。

不要去問TREE(3)有多大,你的腦袋裝不下TREE(3)。
就算把整個宇宙做成一個硬碟,也不可能儲存進去這麽一個數碼。
因此,TREE(3)只能表示為TREE(3),沒有任何其他方式可以精確表示它。
甚至可以說,TREE(3)是只存在於概念裏的,因為你無法用TREE(3)去做任何運算。
TREE(3)減去任何你能寫出來的數碼,都還是等於TREE(3),TREE(3)除以任何你能寫出來的數碼,都還是等於TREE(3)。
在有意義的運算領域,你可以把它當做∞, 因為它會泯滅掉一切實際意義。
當然了,實際上你在自然數軸上隨機取個數,幾乎100%比它大就是了。

真的很令人感慨,不禁讓我想起劉慈欣的【三體】。
當你還只會畫一個角色的時候,仿佛一個太陽在宇宙中踽踽獨行,一片死寂。
當你會畫兩個角色的時候,兩個太陽會彼此圍繞著,單調地旋轉。
而一旦踏入「3」的領域,就仿佛開啟了潘朵拉的魔盒,三個太陽在宇宙中持續那無規律卻又永不重復的狂舞。
幾秒前還是荒蕪一片的沙丘,突然間暴漲至整個宇宙,比兒戲還要荒誕無稽,md像開掛一樣。

TREE(3),如山壓卵,將宇宙碾為齏粉。但是有趣的是,它是有限的。
如果TREE(3)是無限的,那麽無限延伸的角色關系必定包含了此前已被畫出的角色關系。這違背了我們漫畫的分鏡規則。—— 克魯斯卡爾反證法
既然不可能是無限的,那自然是有限的,逆否命題。
同理,TREE(4)也是有限的,TREE(5)亦然。甚至你把TREE(3)打包扔進TREE裏去,結果仍然是有限的。
哪怕你會畫TREE(3)個角色,你都終有一日要無格可畫。
這個推導是嚴謹的,但又頗有點費米悖論的味道。
「如果宇宙無限,那麽必定會有無限多的星球誕生外星人,因此必定會有外星人造訪地球。然而沒有觀測到,所以宇宙有限。」

TREE(3)實在太大,大得匪夷所思。
想要直觀地感受它是不切實際的,我也懶得給各位整宇宙堆沙子的活了。
不是我想偷懶,也不是我幹不來這個活,而是宇宙真的太小了。
為了描述TREE(3),我們必須涉足冰冷的數學,如果不感興趣的可以結束了。
無論如何,我試圖盡量講得通俗易懂

運算是有等級的:
不牛逼級——幼稚園
俗稱掰手指數數,有3個蘋果,再來5個蘋果,
需要掰8次手指。
1級牛逼——小學1年紀
加法: a+b=a+1+\ldots +1 (掰b個1次)
不用掰8次手指,而是直接計算3+5
2級牛逼——小學3年紀
乘法: a\times b=a+a+\ldots +a (b個a相加)
3級牛逼——初中
冪運算: a^{b}=a\times a \times … \times a (b個a相乘)
4級牛逼——大學
叠代冪次: b_{a}=a^{a^{a^{…^{a}}}} =a\uparrow \uparrow b (b個a連續取冪)
是不是見到熟悉的東西了?雙箭頭正是葛立恒數最容易理解的一層。
5級牛逼——博士
指數塔塔: a\uparrow \uparrow\uparrow b = a\uparrow \uparrow\ a \uparrow \uparrow\ …\uparrow \uparrow\ a (a連續巢狀叠代冪次共計b次)
到這裏已經有點難纏了,我們沒辦法一直這麽寫下去。
必須構造一個更加簡明的牛逼公式:
a【n】b =a【n-1】a【n-1】a…【n-1】a (b個a)
這裏的a是底數,【 n 】是牛逼級數,b是執行牛逼運算的底數數目。(超運算)
舉個例子:以2為底,執行4級牛逼運算,共4個底數
2【4】4=2【3】2【3】2【3】2=2^{2^{2^{2}}}=2^{16}
必須提一嘴,牛逼公式裏的a和b每加1,數碼都會變大很多,但是仍然還在可控範圍。但是牛逼級數稍有不慎,就會失去控制。
演示一下:
2【1】4=2+4=6
2【2】4=2\times4=8
2【3】4=2^{4}=16
2【4】4=2^{16}=65536
2【5】4=2【4】65536=2^{2^{2^{…2}}} (65536個2)
2【5】4 有多大?
讓我們沿著天安門廣場的邊,每隔2cm寫個2,寫完廣場的長+寬就能寫完這6萬多層指數塔
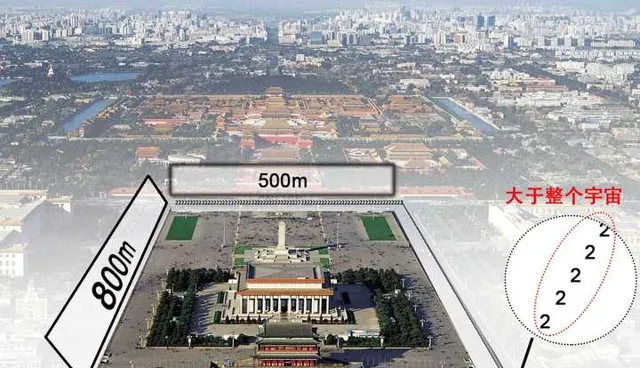
我們無法了解「天安環」有多大,但是我們可以把眼睛聚焦在天安環的尾部。
讓我們看看最後的5層以2為底的指數塔有多大。
2^{2^{2^{2^{2}}}}\gg2^{266}=1.19\times10^{80} (宇宙的基本粒子數目)
因此「天安環」這長達1300多米的指數塔,已經可以把宇宙鞭屍鞭得渣都不剩。
甚至退一步說,哪怕這不是6萬多層塔,而是6萬多位數的2,都足夠把只有80位數的宇宙侮辱了。
不扯遠了,總之,我們的5級牛逼運算,是真的很牛逼。
如果你很會觀察規律,就會猜出6級牛逼運算是巢狀b次的5級牛逼運算,會更加大得無法無天。
至於7級牛逼,8級牛逼那當然更是小母牛坐飛機,牛逼上天了。
講半天牛逼運算是為了幹嘛?
是為了引出阿克曼函數。

阿克曼函數是這麽定義的:
A(x)=2【x+1】x
註意別忘了,【】裏面是牛逼運算級數,後面是底數2的數目。
舉個例子:
A(1)=2【2】1=2\times1=2
A(2)=2【3】2=2^{2}=4
A(3)=2【4】3=2^{2^{2}}=16
A(4)=2【5】4 (我們的「天安環」)
夠嚇人的吧,又是前3個數還整個好活,到了4就局部壞死。
而理解阿克曼函數,是了解如何表達TREE(3)的第一步。

阿克曼函數已經是增長率極其恐怖的函數。
A(x)=2【x+1】x
x每加1,將會同時使得牛逼級數和牛逼次數一起加1。
但是我們的目標是描述TREE(3),這還不夠。
問題不是出在阿克曼函數的增長率小,而是受限於自變量增長的速度太慢。
即便我們把1億當做自變量輸入進去,自變量都不夠大。
我不知道你的腦中是否閃過了一個恐怖的念頭?
沒錯,我們何不把A(4),也就是天安環直接當做x輸入進去?隨後再把A(天安環)的結果當做x輸入進去,如此反復。
人有多大膽,地有多大產!
這樣重復64次的話,就會得到A(A(A(A(A(……………………A(天安環)))))(64層)
簡寫作 A^{64}(4)\approx grahams (葛立恒數),角標代表巢狀次數
是不是很神奇?之前不可一世的葛立恒數,一眼看去也就是個小趴菜。

那麽,終於該說說TREE(3)有多大了。
TREE(3)\approx A^{A(187196)}(1)
註意, A(187196) 這個數碼已經絕對是違法亂紀級別的大數了,G(1)跟它相比和0沒有區別
而此刻它只是個角標,也就是被巢狀的次數。
剛剛構造葛立恒數的約值也就需要巢狀個64次而已。
現在你是要用阿克曼函數巢狀 A(187196) 次!
除了滅絕人性,有悖天綱以外,我不知道該用什麽詞語來形容才好。

我們構造半天,構造了一個出離變態的函數,這個函數是靠著超運算在叠代。
把4當成自變量輸入進去,函數結果就已經是邪魔外道級別。
然後我們決定把邪魔外道當成自變量巢狀進去,得到的產物我已經不知道怎麽描述。
然後我們決定重復這個巢狀的過程,重復的次數竟然……也需要用阿克曼函數來表示……
如果這不叫離譜,那什麽才配叫?

我很少覺得自己表述能力不足,但是我盡力了。
不了解TREE(3)未嘗不是一件好事,如此便不用因渺小而顧影自憐。
人類仰望著TREE(3),心中只有謙卑。
但是,TREE(3)根本沒看見我們。
它不在乎。
【推薦閱讀】
用沙子填滿整個宇宙!
值得一提的是,本文中的TREE(3)的估計值只是一個被認可的TREE(3)的下界。感謝 @紙張山茶花 指出。
筆者不認為目前的人類有辦法精確計算TREE(3)。











