如果是純數學天賦.
無疑目前已知最有數學純天賦的就是這一位.

印度的拉馬努金,雖然拉馬努金成就沒有頂尖王者高斯或者歐拉大,但個人認為純天賦,他無疑是神,最主要體現在他, 完全憑借著直覺 ,締造了兩三千個超前理論公式,卻不知道怎麽去證明,可見他完全是天選之子,他和其他的數學家思維不一樣,通常講,數學是理性且邏輯非常突出的一類學科,其他數學家,基本上都是具有非常強大的邏輯思考的,偏向於證明,而他給人感覺就是靠直覺來判斷.
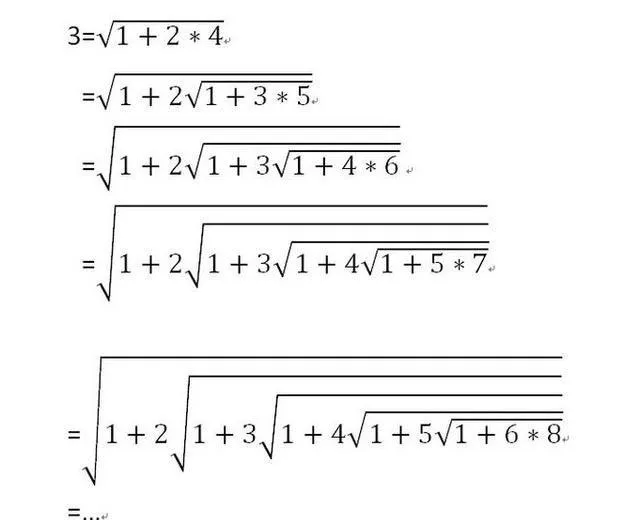
這裏的純數學天賦,就是擁有這樣極其敏感的直覺能力,擁有極強的創造力,尤其是在高等數學之中,越高階越依靠於靈感締造,這樣也是符合人類大腦結構的,我們面對數學難題,要麽就是憑腦海回憶知識鏈熟悉的技巧性,要麽就是突然靈機一動,並沒有那種書本給人的邏輯性,牛頓微積分的締造,當時也沒有完全證明,給他擦屁股的是柯西魏爾斯特拉斯這樣數學家,註意,我們今天的高數是先讀了極限論再學的微分學,從而循序漸進的,可是牛頓當時並沒有極限論,包括歐拉的歐拉公式,在當年復變函數未成型之前,他是怎麽思考的歐拉公式,已不得而知.
如果說邏輯才是數學的王道,那麽電腦早已統治全世界了——靈性的力量.
當然,最佩服的數學家無疑是高斯,是我內心中最具有數學天賦的孩子.
因為喜歡他的傳奇性:
9歲時,發現了高斯求和,即算數級數(等差數列)的求和方法,面對老師的刁難,他用很短的時間計算出了小學老師布置的任務,似乎就是影視劇中的巫師,從1+2+3+4+5+……+100的求和,他所使用的方法是(1+100)+(2+99)+(3+98)+,得……到了結果:5050.

12歲時,已經開始懷疑元素幾何學中的基礎證明.
16歲時,預測在歐氏幾何之外必然會產生一門完全不同的幾何學,即非歐幾裏得幾何學。他匯出了二項式定理的一般形式,將其成功的運用在無窮級數,並行展了數學分析的理論。

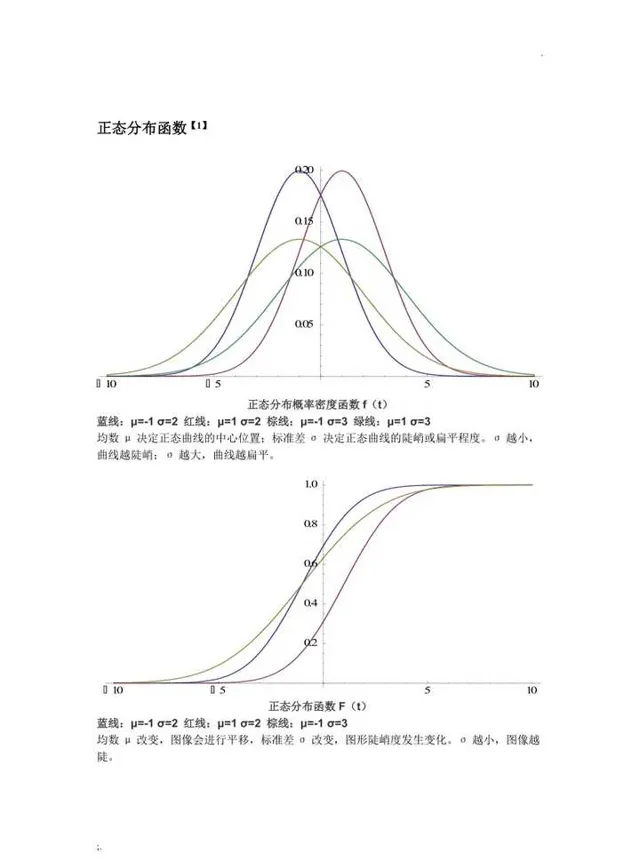
17歲時,發現了質數分布定理和最小平方法。透過對足夠多的測量數據的處理後,並得到高斯正態分布曲線,其函數被命名為標準正態分布,或高斯分布,並在概率計算中大量使用。
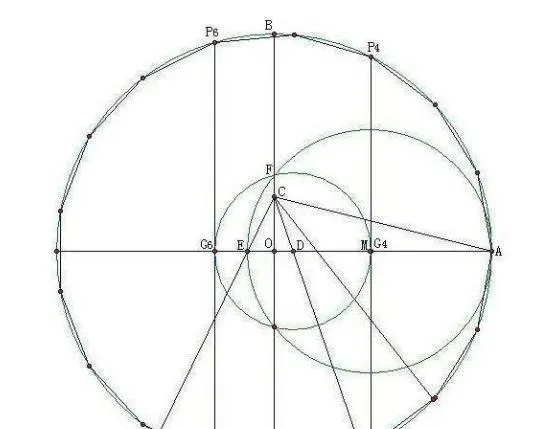
18歲時,一夜之間解決了千年數學難題,連阿基米德,柏拉圖,牛頓……千年內等頂尖大神都束手無策的正十七邊形尺規作圖法,而當時,那僅僅是他的老師和他開的一個玩笑,對於他那僅僅只是個家庭作業.
……
好了主要是書寫童年和少年的高斯.










