歐拉方程式e^(iθ)=cosθ+isinθ是人們公認的優美公式。
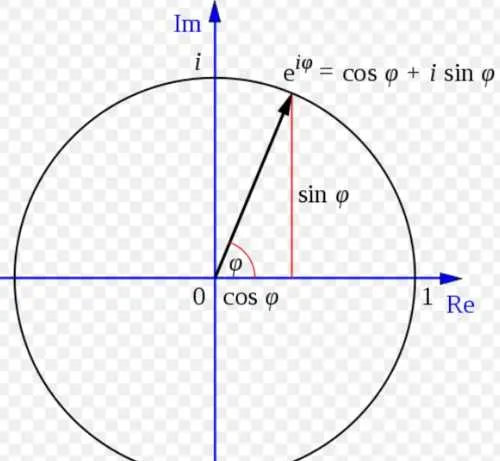
原因是指數函數和三角函數在實數體中幾乎沒有什麽聯系,而在復數體中卻發現了他們可以相互轉化,並被一個非常簡單的關系式聯系在一起。特別是當θ=π時,歐拉公式便寫成了e^(iπ)+1=0,就這個等式將數中最富有特色的五個數0,1,i,e,π,絕妙地聯系在一起。

歐拉方程式是經濟學中的一個重要工具,它描述了個體在面臨不確定性的情況下做出經濟決策的方式。
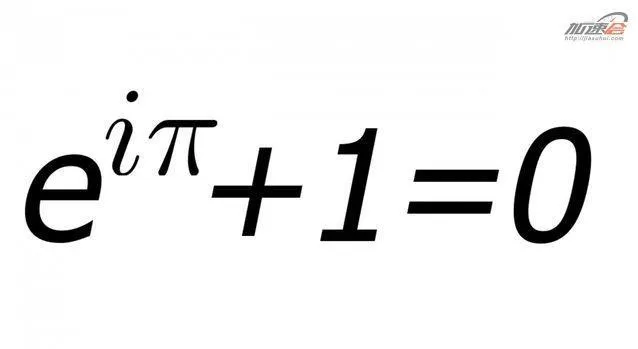
歐拉方程式也是經濟學中一個非常有用的工具,它可以幫助我們理解個體在面臨不確定性的情況下做出經濟決策的方式,以及如何使這些決策最佳化。
具體的形式為邊際收益等於邊際成本。這意味著個體會在邊際成本等於邊際收益的情況下做出最優決策。
歐拉方程式可以套用於許多經濟學領域,如消費、投資、勞動力等。在消費領域,歐拉方程式可以幫助我們理解消費者如何在收入、價格和偏好之間做出最優決策。
在投資領域,歐拉方程式可以幫助我們理解投資者如何在不同的風險和回報之間做出最優決策。
在勞動力領域,歐拉方程式可以幫助我們理解勞動力供給者如何在薪金和休閑之間做出最優決策。
在國際貿易中,歐拉定理可以被套用於解決一些重要的問題。例如,歐拉定理可以幫助經濟學家分析國際貿易中的價格歧視問題,即相同的商品在不同的市場上的價格不同。此外,歐拉定理還可以用於解釋國際貿易的收益和成本等問題。
在金融學中,歐拉定理可以被用來分析股票市場和證券市場的波動。歐拉定理可以幫助經濟學家分析股票價格和證券價格的波動原因,從而得出股票和證券市場的執行規律。此外,歐拉定理還可以被套用於分析股票和證券市場的風險和回報等問題。
歐拉方程式還可以與其他經濟學工具結合使用,如生產函數、成本函數等。例如,我們可以將歐拉方程式與生產函數相結合來解決生產者的生產最優問題。我們也可以將歐拉方程式與成本函數相結合來解決企業的投入最優問題。











