這兩天備課「化學勢」,看了點朗道的書,難免就被帶得往那邊偏了。但不得不承認,朗道式思想確實好用!
- 首先,沒平衡的時候,不能套用熱力學!書中的公式完全不成立。任何公式都是有前提條件的。這個問題反映出提問者的熱力學的基本假設沒學明白,靠刷題是無法真正理解一套理論的。我昨天講的的時候,聽到有學生竊竊私語:「我電動力學沒學,靠刷習題冊過的考試」。這種學習方法讓我非常震驚。曹原開發魔角石墨烯有習題集嗎?愛因斯坦提出相對論,是因為他有一本」相對論習題集「,他把習題集刷到100分,然後就提出相對論了嗎?世界上舍本逐末的事情還真是多啊。。。。。。
2. 考慮一下平衡的時候會發生的情況。根據半經典的統計力學理論,化學勢來自於:
\mu = -k_{\rm{B}} T \ln Z_{1}
對於理想氣體,有:
\mu = -k_{\rm{B}}T \ln \left[ \frac{Ve}{N} \left(\frac{2\pi m k_{\rm{B}}T}{h^2}\right)^{3/2} \right]
換用溫度和壓強作為自變量,就有:
\mu = -k_{\rm{B}}T \ln \left[ \frac{k_{\rm{B}}Te}{P}\left( \frac{2\pi m k_{\rm{B}}T}{h^2} \right)^{3/2} \right]
從這個地方可見, P\to 0 ,化學勢趨於負無窮。貌似出現了反直覺的效果。
但是,這裏有個問題,就是保持溫度不變,壓強要降低,必須改變體積。而保持溫度不變改變體積不能讓體積無限膨脹下去,因為要有環境給它供熱。
另一種思路是保持體積不變,用改變溫度的方法改變壓強。我的經驗是,P 和溫度成簡單冪次關系,這時候,把化學勢裏的溫度用壓強和體積表示,有:
\mu = -P^{\alpha}V^{\lambda} \ln \left[P^{\alpha'}V^{\delta}\gamma \right]
而在有限的冪次下,有: \lim_{x\to 0} x^{\alpha} \ln x^{\alpha'} = 0 ,即化學勢仍然是有限的。
3. 另外,根據上述討論,保持體積不變令 P\to0 時,溫度也趨近於零。由於零點能的存在,溫度不會降到絕對零度,同理壓強也不會降為零。而且這時候需要考慮全同粒子性,並考慮討論的是玻色子還是費米子。對於理想費米子氣體,其零溫下化學勢存在極大值;而對於理想玻色子,由於玻色-愛因斯坦凝聚的存在,其極限值為 0 。總之是不會跑到無窮大去。
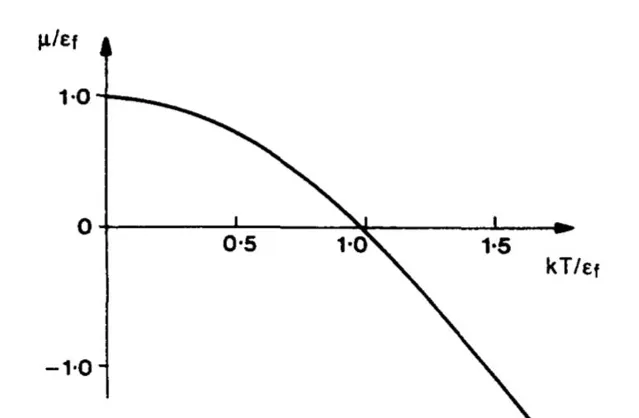
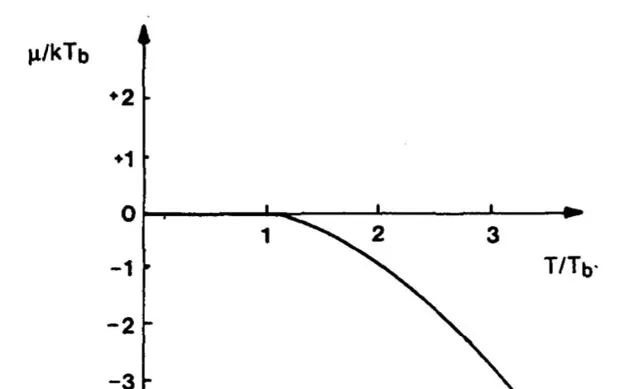
圖來自於文獻:G. Cook & R. H. Dickerson, 「Understanding the Chemical Potential」, Am. J. Phys . 63 , 737 (1995)
4. 對於 自由 光子、 自由 聲子等玻色子,由於粒子數不守恒,其化學勢一直為零。
5. 還有如果粒子數過少,熱力學公式就失效,回到經典力學或量子力學。











