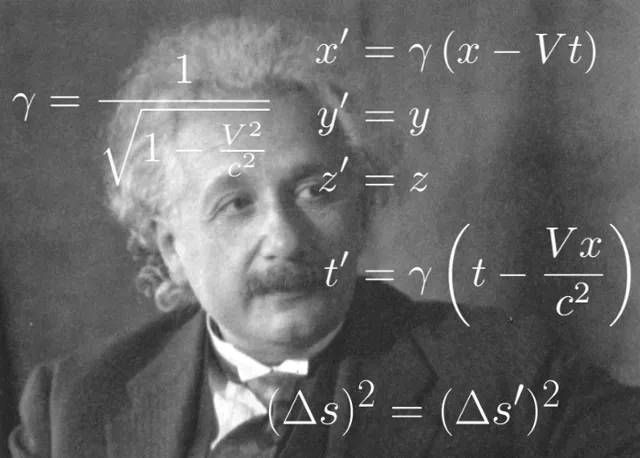
時空圖是狹義相對論中時空性質的圖示。時空圖允許定性地理解相應的現象,如時間膨脹和長度收縮,而不需要數學方程式。在時空圖中,一個物體在所有時間內的位置的歷史軌跡會形成一條線,即該物體的世界線。時空圖中的點表示空間和時間中的固定位置,稱為事件。
最著名的一類時空圖被稱為閔考斯基圖,由赫爾曼·閔考斯基在1908年提出。閔考斯基圖是一種二維的圖,它描述了發生在一個由一個空間維度和一個時間維度組成的宇宙中的事件。與常規的距離-時間圖不同,距離顯示在水平軸上,時間顯示在垂直軸上。此外,時間和空間測量單位的選擇是這樣一種方式 ,以光速移動的物體被描繪成與圖的軸線成45°角。
如何將四維時空形象化?我們不知道,但我們從霍金的話中得到了啟發,他說:
想象四維空間是不可能的。我個人覺得把三維空間形象化已經夠難了,然而,很容易畫出二維空間的圖,比如地球表面。
因此,我們經常使用時空圖(也被稱為閔考斯基圖),沒有x軸和y軸,通常有一個垂直的時間軸和一個水平的空間x軸。
狹義相對論是建立在這樣一個假設上的:對於任何慣性觀察者來說,光的傳播速度都是恒定的。因此,我們需要能夠在時空圖上,畫出光線的路徑。這樣的一條射線可以從x軸上的任何一點開始,沿著x的遞增或遞減方向運動(我們可以想象自己站在x軸的某一點上,沿著x軸向我們的右側或左側發射一束光)。
在時空圖上畫出光路線徑的困難在於,因為光的傳播速度非常非常快,如果我們用國際單位秒和米作為兩個軸的話,表示這條路徑的線應該盡可能接近水平線。
為了解決這個問題,我們將以秒為單位的時間乘以以米/秒為單位的光速,並使用這個量ct作為垂直時間軸的單位。ct的單位是光速乘以光傳播1米所需的時間t,即1。透過使用時間的ct單位,我們將光速c定義為1,現在可以把光線的路徑畫成斜率為45度的直線,向左或向右,取決於它的運動方向。
記住,ct中的t仍然是指時間單位秒,但是一個單位的ct不是1秒,而是3 × 10^(-8秒),這個數值要小得多。在相對論中,使用米作為時間和距離的單位是一種方便而普遍的做法。閔考斯基空間中的單個點被稱為一個事件,它有四個組成部份ct,x,y,z,用指數標記法記作:
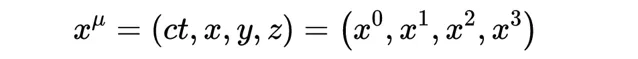
其中:
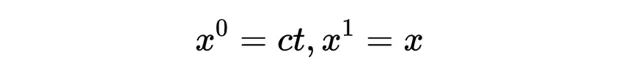
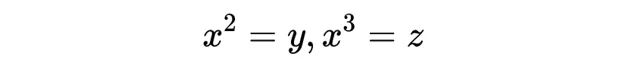
x_μ有也也被稱為時空的「四位置」。閔考斯基空間中的一條線代表粒子在時空中的運動(有點像蒸汽軌跡顯示噴射飛機的路徑),被稱為粒子的世界線。
時空圖的基本概念
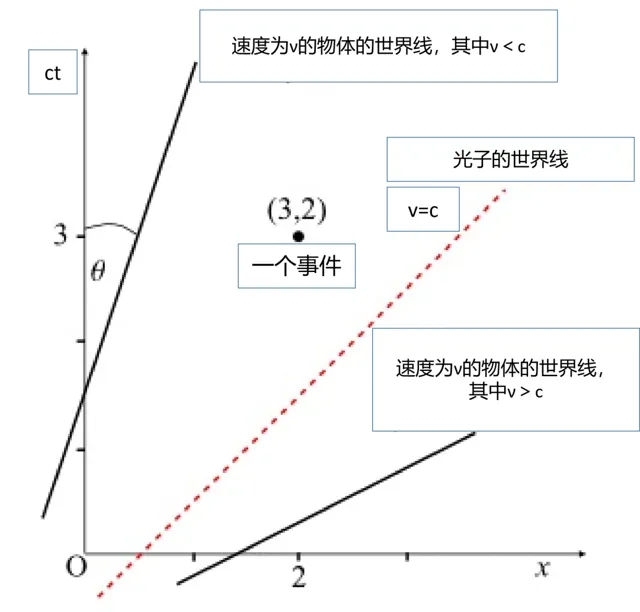
座標系S中觀察者的一個簡單的時空圖
上圖表示在慣性參考系S下觀察者O的二維時空切片。空間中的單個點是一個事件,它在x的某個值處瞬間發生。例如點(3,2)描述時空中的一個點,它的時間座標為ct = 3,空間座標為x = 2。
因為我們使用的是ct時間單位,一條45度的直線表示光線的路徑。我們可以畫出無數條這樣的線,每條線代表從ct = 0時的不同x值開始的光線。以小於c的勻速運動的物體與x軸成大於45度角的直線。
如果一個物體以恒定速度v運動,那麽這個速度等於移動的距離除以所花費的時間,得到:
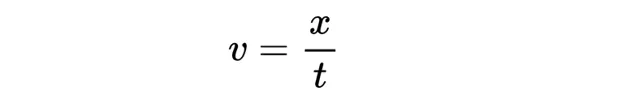
物體將有一條與ct軸夾角θ的直線,其中:
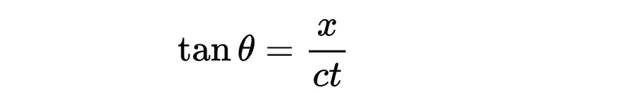
從而:
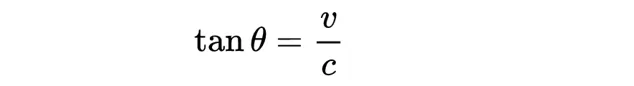
增加一個觀察者
我們如何表示第二個觀察者O'所在的慣性系S'呢?首先,為了簡化工作,我們假設兩個座標系都是標準構型,並且座標系S'相對於座標系S以恒定速度v移動。
我們可以先畫出座標系S'的ct'時間軸。但是我們如何在圖中畫出這個軸呢?
首先,因為我們使用的是標準構型的座標系,我們知道座標系S和S'的原點在座標系S中的時間ct = 0和座標系S'中的時間ct' = 0時重合。因此,ct'軸必須透過座標系S的原點。
其次,考慮當空間座標x' = 0時,在座標系S'中可能發生的所有事件。所有這些點連線在一起,就構成了ct'軸。但x' = 0點沿著ct'軸以速度v移動。因此,我們可以畫出ct'軸作為移動點x' = 0的世界線。ct'軸與座標系S的縱ct軸成角度θ:
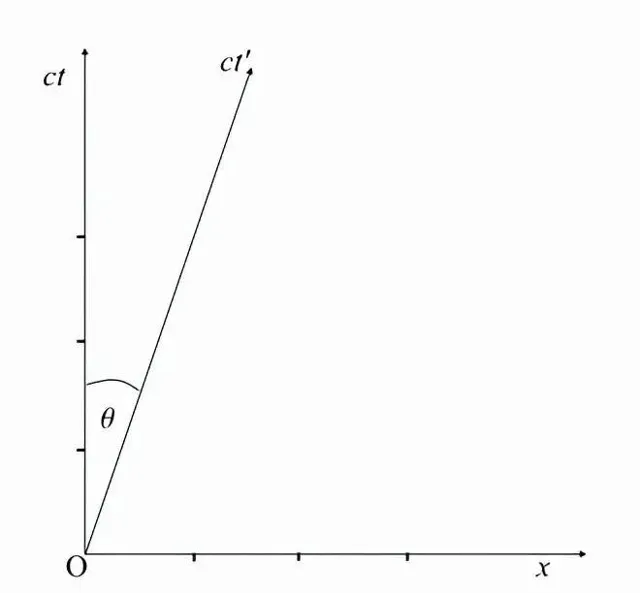
第二個參考系S'的ct'時間軸
我們現在需要畫出座標系S'的x'軸。這個軸可以將所有的事件連線起來,時間座標為ct' = 0。但是該怎麽做呢?對於ct'軸,我們知道x'軸必須透過座標系S的原點,因為處於標準構型。
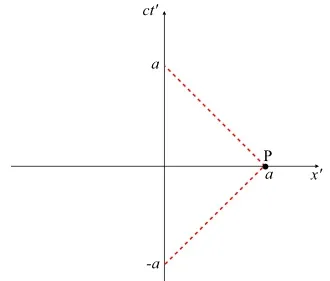
反射光線的路徑
回想一下,狹義相對論的一個假設是光速c對所有慣性觀察者來說都是一樣的。這意味著,對於任何慣性座標系,任何光線的斜率都是45°。上圖顯示了觀察者O'的時空圖(軸ct'和x')。折線表示x' = 0, ct' = -a處發射的一束光線,照射在x' = a, ct' = 0處的一面鏡子上,反射回x' = 0,ct' = a。我們稱x' = a, ct' = 0處的點(或事件)為P。隨著a的變化,P點的位置也會變化。事實上,由於光速的恒定,對於a的不同值,P點(ct'總是等於0)沿著x'軸移動。
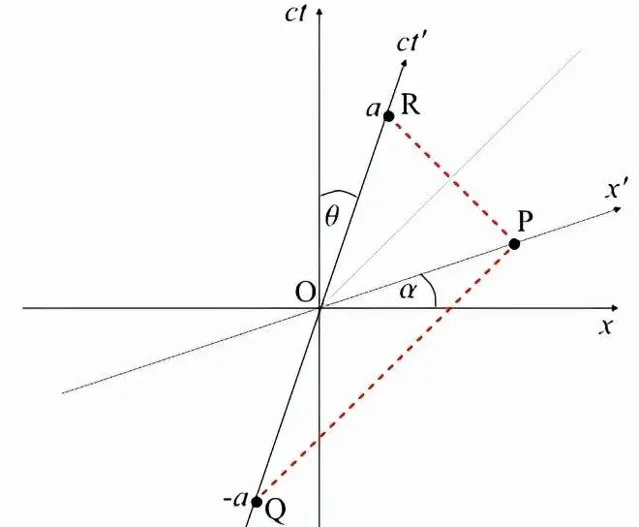
第二座標系S的x'軸
我們使用點P的這個內容來定義x'軸的位置。這次我們回到了觀察者O的參考系S,它顯示了在點Q (x' = 0,ct' = -a)發出的一條光線(折線)擊中了點P (x' = a,ct' = 0)的鏡子,然後反射回點R (x' = 0,ct' = a)。
三角形ORP是一個等腰三角形,被一條與x軸成45°的線平分並穿過O。因此,x'軸與x軸的夾角必須與ct'軸與ct軸的夾角相同,也就是θ=α。
因此我們可以說x'軸的方程式是:
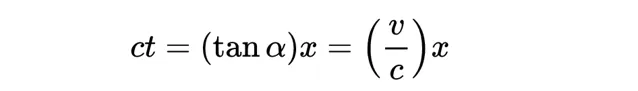
而ct'軸的方程式為:
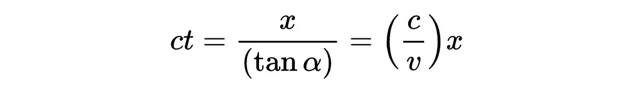
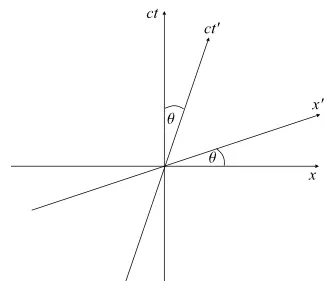
觀察者O的時空圖
上圖顯示了從O(從S參考系)的角度來看的參考系S和S', O'所在的參考系S'向右移動。
同樣的物理情況如下圖所示,但這一次從O'的角度來看,他看到O向左移動。
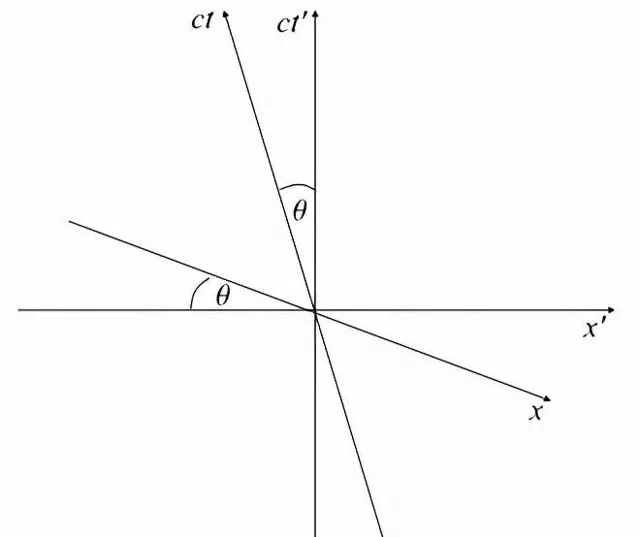
觀察者O'的時空圖
這可能有點讓人困惑。我們有一個慣性系S,它的座標軸是x和ct,還有另一個慣性系S’(相對於S以勻速v運動)它有自己的座標軸x’和ct’,都畫在同一個圖上。我們現在如何描述一個特定事件的座標?
這是簡單的。我們需要做的就是構造平行於座標軸的座標線。以下圖所示的事件A為例:
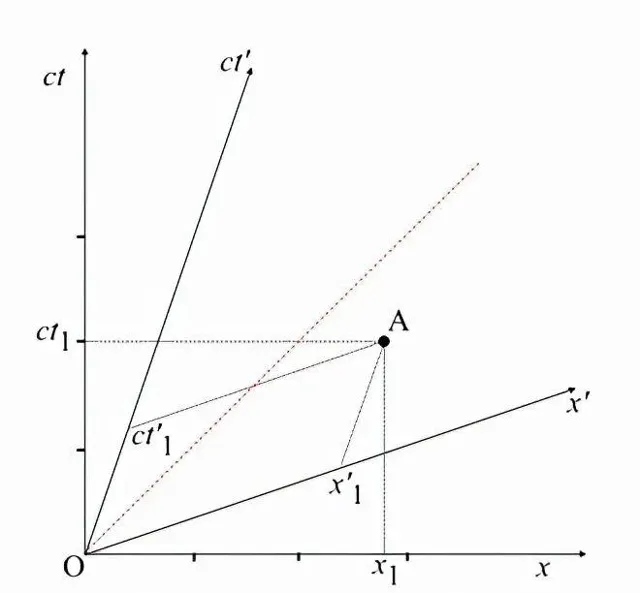
我們通常讀取A關於x和ct軸的座標(就像我們在任何笛卡爾座標上做的那樣),它們是x_1和ct_1。然後我們畫一條穿過A平行於x'軸的直線。這條線與ct'軸的交點就是ct'座標,即:
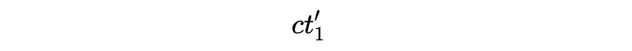
類似地,我們接著構造一條穿過A並平行於ct'軸的直線。這條線與x'軸的交點就是x'座標:

這裏值得註意的是,x'和x軸並不重合。如果我們使用伽利略變換,它們就會重合,當然,伽利略變換是基於伽利略/牛頓對絕對時間和空間的假設。在這種情況下,我們仍然會畫一個傾斜的t'軸(其中t' = t),但x'和x軸將在同一條線上(其中x' = x - vt)。
第二個假設(光速的恒定)要求有一個傾斜的x軸,並破壞了所有關於絕對時間和空間的假設。根據繪圖的準確性,並假設我們知道如何校準ct'和x'軸,我們可以估算出觀察者在S和S'參考系上測量到的事件A的座標。從圖表中測量當然不是很準確。後面,我們討論勞侖茲變換, 它允許我們用代數方法計算在不同慣性系中的觀察者的測量值,包括校準ct'和x'軸。
同時性與因果關系
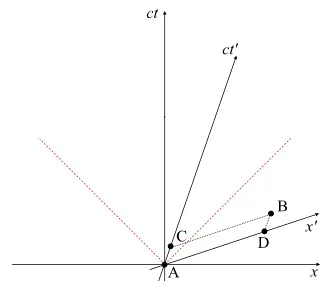
同時性的相對性
我們現在可以證明一個令人驚訝的結果,即事件的同時性可以依賴於觀察者的參照系。 上圖顯示了四個事件A,B,C,D。它們發生的順序是什麽?
慣性系S中的觀測者O將按照A、C、D、B的順序(隨著時間ct的增加)分別看到事件的發生。然而,慣性系S'中的觀測者O'將使用ct'軸來記錄他的時間,首先會看到A和D同時發生,然後看到C和B同時發生。由於兩個觀察者不共享一個共同的時間軸,一個觀察者同時發生的兩個事件對另一個觀察者來說也不可能同時發生。這種現象被稱為 同時性的相對性 。
如果兩個事件同時發生在空間的同一點上,所有的觀察者都認為它們是同時發生的。如果事件在空間中是分離的,那麽它們是否同時發生取決於觀察者的參照系。
我們還可以從上圖中看到,兩個觀察者不僅會在哪些事件是同時發生的問題上產生分歧,而且在C和D的情況下,他們甚至不會看到事件以相同的順序發生。這個結果比同時性的相對性更奇怪, 因為它似乎推翻了因果關系的基本概念 。事件X只能導致事件Y,如果X發生在Y之前。假設X是我掉書的事件,Y是書掉到地板上的事件。如果一個觀察者不能同意我的觀點,我們可能會以一種奇怪的情況結束,他們先看到書掉到了地上,然後看到我掉了一本書。
幸運的是,狹義相對論的結果之一是,在觀察者的慣性系中,沒有任何資訊訊號或物質物體的傳播速度能超過光速。這意味著,盡管觀察者可能對兩個事件的順序有不同意見,但他們不會對兩個由光訊號聯系起來的事件的順序有不同意見。
在觀察者的慣性系中」的條件是至關重要的。在不斷膨脹的宇宙中,正如我們在宇宙學中所看到的,星系可以以大於光速的速度遠離我們。然而,這種運動並不在任何觀察者的慣性系中,因為它是空間本身在膨脹。
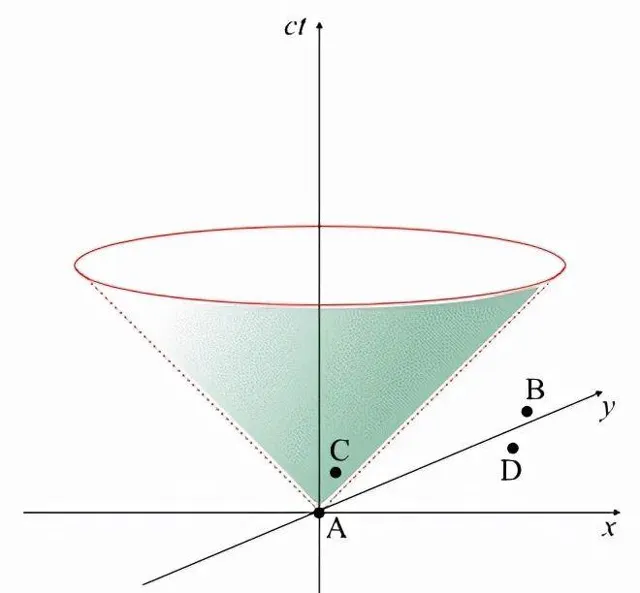
光錐
光錐 是由透過A的光線(兩個虛線)繞ct軸旋轉而形成的(y軸表示光錐占據了兩個空間維度:x和y)。假設這四個事件仍然位於x軸的正上方,我們現在看到,在B、C和D之外,唯一可以透過不超過光速的訊號與A聯系在一起的事件是C。這是因為只有C在光錐的「內部」。換句話說,因為沒有訊號能比光傳播得更快,所以A唯一可能引起的事件就是C。事件,比如A和C,位於彼此的光錐內,被稱為因果關系。如果兩個事件在一個慣性系中有因果關系那麽它們在所有慣性系中也有因果關系。
如果任何事件,如B,在A的光錐內,可以透過A(一個事件在原點)和B畫一個ct'軸。這意味著有一個慣性系,A和B在不同的時間出現在相同的地方。
相反,只有比光速快的訊號(與x軸成45°的直線)才能將A和B, A和D, C和D聯系起來。所以這些事件沒有因果關系。由於C和D之間沒有可能的因果關系,因此,在任何參考系下,我的書都不會在掉到地上之前就掉到地上。
如果任何事件,如C,是在A的光錐外,則有可能透過A(在原點的事件)和C畫一個x'軸。這意味著在某個慣性座標系中,A和C同時發生但在不同的地方。
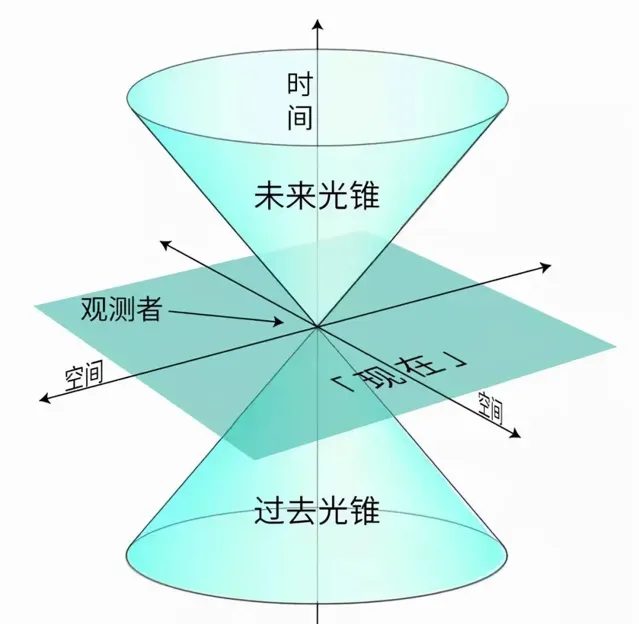
光錐(上圖)在相對論中是一個非常有用的概念,它在三維空間中顯示了那些事件的位置,這些事件可能與現在發生在原點的事件有因果關系。光錐的側面是由穿過原點的光線形成的。原點下方的錐體表示過去可能導致原點事件的事件。原點上方的錐體包含可能由原點事件引起的事件。一個透過原點和x、y軸的平面代表現在。
間隔不變性
觀察者O和O'將使用不同的座標值描述上面提到的四個事件A、B、C、D的位置。但是,他們會同意兩個事件之間的時空分離,其中間隔∆s^2為:
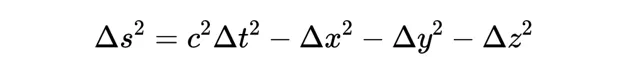
這個定理被稱為間隔的不變性,我們將在後續的文章中用勞侖茲變換來證明它。我們說間隔是不變的,因為任意兩個不同的慣性觀測者計算∆s^2,將得到相同的答案。
時空間隔∆s^2的值可能是正的、負的或零的,最好把它看作一個單獨的符號,而不是某物的平方。在原點處的事件A與時空中其他事件的三種關聯方式是:
類時間間隔,其中∆s^2>0,描述了A光錐內的事件。這些事件與A是有因果關系的,會有一些慣性系,A和C在同一地點,但在不同的時間發生。
類空間間隔,其中∆s^2<0,描述了A光錐外的事件。這些事件與A沒有因果關系,會有一些慣性系A和C同時發生但在不同的地方。
類光間隔,其中∆s^2=0,描述了A光錐上的事件。這些事件與A有因果關系,但它們只能透過一個光訊號與A聯系起來。
間隔不變性是狹義相對論中最重要的定理。
不變的雙曲線
現在我們已經知道,時空間隔對於任何慣性觀測者都是不變的,我們可以看到如何在時空圖上校準座標系S'的x'和ct'軸。考慮以下方程式:
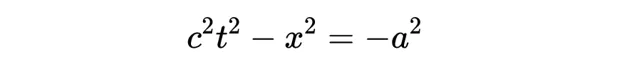
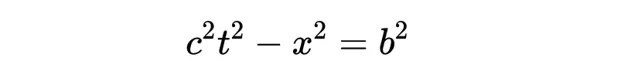
這兩條曲線都定義為觀察者O的時空圖上的雙曲線(奇異雙曲線)。如下圖所示:
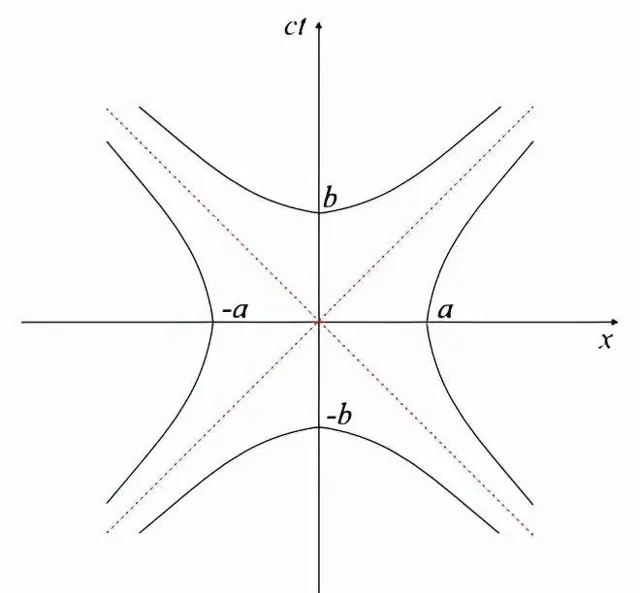
上圖顯示了座標系S'相對於座標系S作勻速相對運動。我們試圖校準座標系S'的ct'和x'軸。考慮穿過事件A和B的不變雙曲線:
事件A在ct軸上,因此x = 0。如果我們讓事件A發生在ct = 1,那麽b^2, A到原點的類時分離,也必須等於1。因為雙曲線將所有具有相同時空間隔的事件連線起來,所以ct'軸上的事件B (x' = 0)也必須在ct' = 1時出現。
類似地,穿過事件C和D的不變雙曲線:
將事件以-a2相同的類空分離連線起來。如果我們讓C在x = 1處出現,那麽ct = 0,(-a)^2一定等於-1。事件D,在同一個不變雙曲線上,也必須出現在x' = 1處(其中ct' = 0)。
註意到D看起來比C離原點更遠,盡管它們有相同的時空間隔。類似地,B和A與原點的時空分離是一樣的,盡管B看起來更遠。這些困惑源於這樣一個事實: 我們試圖在一個平坦的歐幾列特曲面上表示非歐幾列特時空 。我們說的非歐幾裏得是什麽意思?意思是任意兩點之間的距離不是由歐幾列特線元ds^2 = dt^2 + dx^2表示的,而是由非歐幾列特線元ds^2 = dt^2 - dx^2表示的。 負號決定了一切 。我們可以用不變雙曲線來說明 間隔 不變性的兩個重要物理含義: 時間膨脹和長度收縮。
時間膨脹
上圖顯示了在ct = 1處穿過ct軸的不變雙曲線,ct'軸在ct' = 1處。透過事件A和C的水平虛線是觀察者O的同時線,這意味著該線上的所有事件都具有相同的時間值ct = 1。透過B和D的傾斜虛線(實際上與雙曲線B相切)是一條觀測者O'的同時線,這意味著這條線上的所有事件都具有相同的時間值ct' = 1。這兩位觀察者測量到的是什麽?
觀察者O'測量ct'軸上ct' < 1時發生的事件C。然而,觀察者O在其ct軸上測量ct = 1時發生的相同事件。從O的角度來看,S'參考系中屬於O'的時鐘執行緩慢。黑色箭頭 TD 是O觀察到的時間膨脹。
觀察者O測量ct軸ct < 1時發生的事件D。然而,觀察者O'在ct'軸上測量ct = 1時發生的相同事件。從O’的角度來看,S參考系中屬於O的時鐘執行緩慢。黑色箭頭 TD' 是O'觀測到的時間膨脹。
令人矚目的結果是,兩個觀測者都測量到對方的時鐘執行得很慢!這種效應被稱為 時間膨脹 。
長度收縮
上圖顯示了x = 1處經過x軸和x'軸x' = 1處的不變雙曲線。垂直的虛線穿過事件B和C,對於觀察者O來說x = 1是一個常量。透過A和D的斜線虛線(實際上與D點的雙曲線相切)平行於ct'軸,因此對於觀察者O'來說x' = 1是一個常量。這兩位觀察者測量到的是什麽?
觀測者O'在x'軸上測量x' = 1時的距離OD。點A對於O'也有相同的x' = 1,因為它在直線AD上。然而,觀察者O在其x軸上測量的距離與OA < 1相同。從O的角度來看,OD = 1的距離縮小為OD < 1。黑色箭頭LC是O所觀察到的長度收縮。
觀測者O在其x軸上以x = 1測量距離OC。點B的x = 1與點O相同因為它在直線BC上。然而,觀察者O'在其x'軸上測量的距離與OB < 1相同。從O’的角度看,OC = 1的距離縮小為OC < 1。黑色箭頭LC'是O'觀察到的長度收縮。
兩個觀察者都測量運動物體在運動方向上的收縮,這種現象被稱為 長度收縮或勞侖茲收縮。
我們必須認識到,時間膨脹和長度收縮都是真實的、可觀察到的效應,而不是由錯誤的時鐘、不可靠的尺子或光從一個移動的事件傳播到一個觀察者所花費的時間造成的光學錯覺。一名太空人乘坐火箭以接近光速飛過地球時,會看到這顆行星沿著她飛行的方向被擠壓。
看到被壓扁的地球意味著你正在以接近光速的速度移動
當然,我們在日常生活中不會註意到這些現象,因為我們的相對速度並不接近光速。
相對論數學原理(一),為什麽首先要解決數學問題
相對論數學原理(二),擯棄常識與偏見











