看著好像沒幾個正經的答案,那就勉強答一發吧。
時間座標2019-2020,當時Quantum Information課設跟著兩個隊友準備搞點事情,開始選題的時候心潮澎湃.....Shor/HHL//VQE/QAOA...etc(均為各種花裏胡哨的量子演算法),後來發現能用的physical qubit頂多三五個...人都裂了
Sycamore和IBM的premium硬件是肯定用不起的,作為窮學生,只能玩開放的免費硬件。當時IBM的開放硬件大概是Yorktown,Athens那一批 [1] ,就三五個位元,教授自己實驗室的Quantum Inspire [2] 也不太行
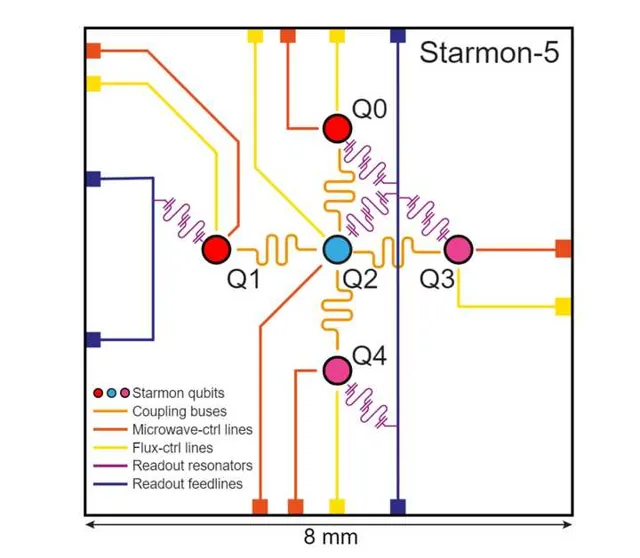
就這三五個位元fidelity還差的離譜...而且還沒有全聯通(比如見上圖),遠距離的qubit做門只能花式SWAP....
ps想放個當時fidelity的數據在這的,好家夥一看IBM的硬件現在都27個qubit了,老硬件都淘汰了,離譜....勉強拿Santiago的數據看一下吧
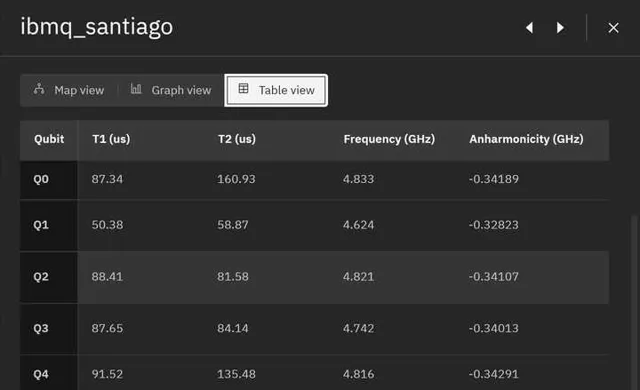
Santiago的CNOT的error大概在1e-3這個量級,比起當時用的來說已經高了不少...
(personally我覺得這玩意完全不能叫量子電腦,頂多叫可控多位元系統)
沒辦法只能變著花在這幾個qubit上搞點東西出來...當時想的是大規模的路線效果估計也不好,那就整點toy model做做benchmark....看看跟預期結果差多少。
然後就跟室友整了個非常弱智的路線,近似複制演算法(Quantum Approximate Cloning Machine , QACM) [3] 。根據non-cloning theorem,量子態是不可能被完美復制的,但是我們可以透過QACM提取出最大上限的量子資訊然後復制一個近似的態,這個態的fidelity理論上限是5/6
這玩意的路線大概是這樣的
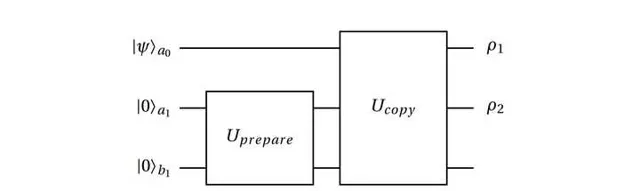

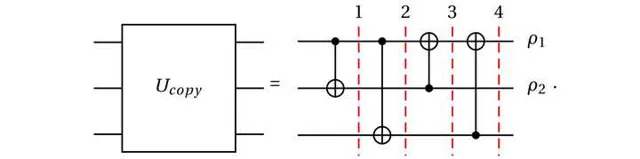
你沒看錯,這玩意一共用了3個qubit,一個目標輸入 a0,一個復制輸出 a1,一個ancilla(輔助位元)b1。這個路線實際實作的是一個projective measurement+copy的過程。因而輸入態a0的資訊必然會有所損失,最終實作的結果是 \rho_1=\rho_2
好了,重點來了, 寫程式碼是什麽體驗?
答案是根本沒啥體驗,因為完全算不上程式碼....
大部份雲平台的都采用的視覺化editor,滑鼠上去拖兩下就完事了,比如IBM Q Experience的界面如圖

當然如果你實在想不開的話也可以去寫QASM,大概是這樣的
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
ry(0.1415394733244273) q[0];
rx(-1.5707963267948966) q[0];
sdg q[1];
h q[1];
tdg q[1];
cx q[0], q[1];
t q[1];
h q[1];
s q[1];
cx q[1], q[0];
rx(1.5707963267948966) q[0];
ry(-0.1415394733244273) q[0];
rx(1.5707963267948966) q[1];
ry(-0.1415394733244273) q[1];
measure q[0] -> c[0];
measure q[1] -> c[1];
或者用Qikist的py介面,
from qiskit import QuantumRegister, classicalRegister, QuantumCircuit
from numpy import pi
qreg_q = QuantumRegister(2, 'q')
creg_c = classicalRegister(2, 'c')
circuit = QuantumCircuit(qreg_q, creg_c)
circuit.ry(0.1415394733244273, qreg_q[0])
circuit.rx(-1.5707963267948966, qreg_q[0])
circuit.sdg(qreg_q[1])
circuit.h(qreg_q[1])
circuit.tdg(qreg_q[1])
circuit.cx(qreg_q[0], qreg_q[1])
circuit.t(qreg_q[1])
circuit.h(qreg_q[1])
circuit.s(qreg_q[1])
circuit.cx(qreg_q[1], qreg_q[0])
circuit.rx(1.5707963267948966, qreg_q[0])
circuit.ry(-0.1415394733244273, qreg_q[0])
circuit.rx(1.5707963267948966, qreg_q[1])
circuit.ry(-0.1415394733244273, qreg_q[1])
circuit.measure(qreg_q[0], creg_c[0])
circuit.measure(qreg_q[1], creg_c[1])
但是實際上搞這些沒什麽意義,因為量子路線的QASM完全不具備任何可讀性。畢竟QASM只封裝到了門(quantum gate)的級別,而量子門對標的是經典數碼電路的邏輯門(與或非,NOT,AND,NAND etc),連組譯都算不上..... .
手寫組譯已經很反人類了,設計邏輯電路emmmm,只能說目前這個領域還停留在EE級別,跟CS和所謂的程式碼完全沒得關系,請各位程式設計師老哥別給自己加戲。
非要說寫程式碼的話大概就是拿qiskit的api寫個指令碼,調IBM的硬件,因為當時掃的參數比較多,還整了個batch改參數....導致那幾天IBM Q的後台基本都是400+的排隊
在當下這個階段,設計演算法重要的不是寫程式碼,而是理解推導quantum circuit,而這一過程是非常數學且反直覺的,比如上面那個看起來很弱智的copy路線的推導如下
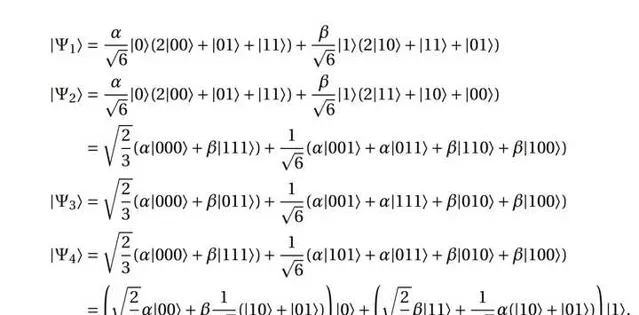
以上的 |\Psi_1\rangle,|\Psi_2\rangle,|\Psi_3\rangle,|\Psi_4\rangle,|\Psi_5\rangle 分別為copy子路線中五條標記的紅線位置處的量子態。
量子路線的推導是這樣的,先把初始的量子態寫出來(很多時候是疊加態)然後每經過一個門就跟根據相應的門操作對態做一次變換,然後把新的態寫出來。直到推導完最後一個門。
題主問會不會處理疊加態變量,的確是會處理的,但是這個過程更多是提前做的數學推導,然後發現這一套門的確能取得我們想要的效果,之後要做的就是把門排列起來。
所以說在量子電腦上寫程式碼不存在的,只有數學推導和排門電路兩個過程。
pps. 補充一下,手滑把路線的圖貼錯了,當時一共做了三種路線,QACM,還有兩種變體 Phase-Covariant QACM (用於復制XZ軸上的態)以及Economical QACM(經濟型,即只有兩個qubit)...貼的是EQACM的
ppps. 再補充一下,如果路線規模大了的話再手排門效率會低很多,這時候的確可以用到一些基本的封裝比如量子傅立葉變換路線(QFT,路線排列方式是固定的)。但是目前我暫時還不了解有帶封裝的高級語言,因為NISQ時期能用的qubit的確太少了。
不過諸君也能看出來,量子計算領域的進步還是非常神速的,最起碼IBM Q的qubit數量已經翻了好多倍了(至於fidelity能不能擺脫隨機數發生器的範圍那就另說了,有空可以跑個QAOA試試
以上
參考
- ^https://quantum-computing.ibm.com/
- ^https://www.quantum-inspire.com/about-qi/
- ^https://journals.aps.org/pra/abstract/10.1103/PhysRevA.62.012302










