講真,對這個問題感興趣,還點進來看的人,都不是一般人。^_^
簡單的說,早期的古代數學多數是 發現 ,但是從2000多年前的古希臘開始,數學家們創造出大量超越自然的新事物,導致此後的數學越來越多的是 發明 。

圖片出處:https:// commons.wikimedia.org/w iki/File:La_scuola_di_Atene.jpg
古希臘的先賢們也不會想到,他們居然為人類開辟出一片新的世界。
在這個新世界中,人類的思想得到了前所未有的解放,並加速了科學與技術的進步,讓人類文明進入了快速騰飛的時代。
一切先從定義開始
數學究竟是發現(discovered),還是發明(invented),取決於「發明」和「發現」的定義。
先看兩個案例:
透過這個例子,我們可以達成共識:
如果以這兩個定義為基礎,可以推出:
因為,數學的定義、符號和規則都是人類的發明,是自然宇宙中以前不存在的事物。
所以,數學是人類的發明,而不是發現。
Q.E.D.
等一下,這樣就證明結束了嗎?
並沒有,因為事情沒有這麽簡單。
有限的自然宇宙和無窮的數學宇宙

「無窮」是數學中最核心的概念之一,但是「無窮」只存在於人類的想象中,不存在於自然宇宙中。
在我們的印象裏,自然宇宙是無窮的。
然而,隨著人類觀測能力的增強,天文學家逐漸發現,越來越多的證據表明,宇宙是有限的,我們所生活的自然宇宙,實際上比我們 想象 的要「小」的多。
天文學家是如何發現宇宙是有限的,這是一段很有趣的歷史,篇幅原因不在這裏展開,推薦一部精彩的BBC紀錄片【萬物與虛無】(Everything and Nothing),非常通俗和系統的介紹了這段歷史,你可以在B站上找到。

根據天文學家觀測到的天文數據,科學家發現宇宙的時間不能無限上溯,而是存在一個叫「大爆炸」的起點,宇宙的年齡估計不超過200億年;宇宙的空間也非無限,宇宙的直徑不超過1000億光年;而宇宙裏所有普通物質的質素是1.45×10^{53} 千克,盡管這些都是極其龐大的天文數碼,但也是有限的。[1]
也就是說,我們印象裏那個無窮的宇宙,是我們想象出來的。
宇宙中所有已知的自然事物,包括時間、空間、物質、能量……等等都是有限的,在自然中並不存在無窮的事物。
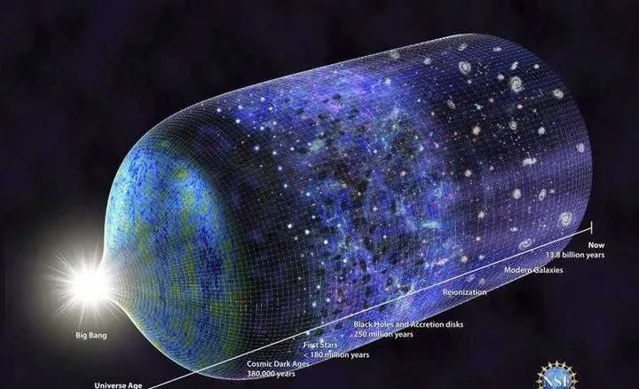
圖片出處:What Really Put The 'Bang' In The Big Bang?
然而,相比於自然,在數學的世界裏, 無窮 幾乎無處不在 。
簡單的,如分數1/3,就可以表達為 無限 迴圈小數0.3333……
常見的,如圓周率π,則是一個 無限 不迴圈的常數,這個數就蘊含著無窮。

圖片出處:How to make the digits of π go around in a spiral like this?
人類至今也無法窮盡圓周率的計算,並不是因為它難算,而是因為人類所擁有的能量和物質是 有限的 。
不要忘了,無論是電腦,還是人腦,在計算時都需要 消耗 能量和時間,而儲存數據時,也要 占用 物質和空間,所以人類的算力不能無限的增長。
事實上,即使人類窮盡宇宙裏所有的能量,即便計算到宇宙淪陷,也無法計算出圓周率的最後一位;即便耗盡所有的物質,寫滿了宇宙所有的空間,也無法把圓周率計算的數據保存下來。
因為無窮是沒有盡頭的!
請仔細想想,是不是這樣!
僅僅是數學世界中一個常見數碼的計算,就可以耗盡我們這個自然宇宙中所有的能量、物質、時間和空間。
有趣的是,數學家還證明了,像π這樣的無理數,其個數要遠遠多於有理數。
更有趣的是,有的無窮比另外一些無窮還要大,比如說自然數的個數有無窮多個,而實數的個數卻遠比自然數多的多。
這些無窮,都是人類在數學世界裏證明和 創造 出來的新概念,它們在自然宇宙中並不存在,是人類在對自然宇宙觀察和思考後,在數學世界中重新 發明 的新事物。
換句話說,數學世界和自然世界是截然不同的兩個世界,數學是人類創造出來的 全新世界[2] 。
無窮讓數學淩駕於其他科學之上
公元前6世紀,古希臘人證明出了第一個數學定理,從此,無窮進入了數學。
第一個定理是泰勒斯證明出來的泰勒斯定理,和他同時代的畢達哥拉斯則證明了勾股定理,並建立了第一個數學學派。

(維基百科說圖中抄作業的是阿那克西曼德,但他比畢達哥拉斯要早,我更傾向於是德謨克利特,反正拉斐爾也沒明確他是誰)
畢達哥拉斯用邏輯推理的方式,證明了直角三角形都遵循勾股定理。
這裏針對的「直角三角形」並不是指某 一個 直角三角形,而是指 所有的 直角三角形,對 無窮多 的直角三角形都成立,不存在例外。
正是因為畢達哥拉斯的這個貢獻,他和泰勒斯都被戴上了「第一位數學家」的桂冠。
在他們之前的古巴比倫、古埃及的數學家,都無法獲得這個殊榮,盡管他們提前一兩千年就發現了這些 定律 ,但是他們並沒有把定律證明成 定理 。(當然很可能他們也證明了,只是還沒有足夠的證據支持)
是無窮讓定律和定理之間 產生了天壤之別。
所以,畢達哥拉斯之前的古代數學家更多的是發現,他們 發現 了很多定律,但是沒有發明太多超越自然宇宙的數學概念。
而畢達哥拉斯之後的數學家,引入了演繹和無窮,還定義了很多超越自然的概念,導致此後的數學越來越多的是發明。
這是一個歷史性的時刻,古希臘哲學家開辟了一個 無窮的新世界 ,而數學也從此開始淩駕於其他科學之上。
高斯稱,「數學是科學的皇後」( Regina Scientiarum)。
而愛因斯坦也表示認同[3]
數學之所以擁有超越其他所有科學的地位,是因為數學中的法則是絕對確定和無可質疑的,而其他科學的法則則是可質疑的,並隨時有被新發現的事實所推翻的危險。One reason why mathematics enjoys special esteem, above all other sciences, is that its laws are absolutely certain and indisputable, while those of other sciences are to some extent debatable and in constant danger of being overthrown by newly discovered facts.
大部份自然科學中的定律,放在數學中只能算作 猜想 。
因為這些定律都是觀察、歸納而來的,還不能靠嚴格的證明保證其永遠成立。
例如以牛頓定律所構建的經典力學,後來就被相對論和量子力學所覆寫。
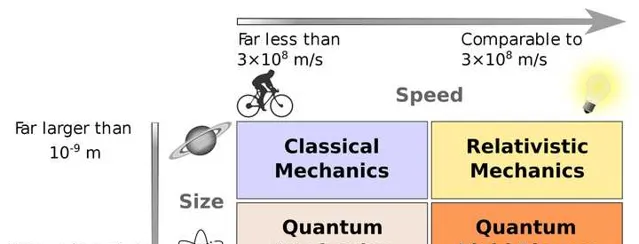
圖片出處:https:// en.wikipedia.org/wiki/M odern_physics
數學的地位要歸功於無窮,數學家赫爾曼.外爾(Hermann Weyl )也說[4]:
數學被稱為關於 無窮 的科學。的確,數學家發明了有限構造,透過該構造可以解決問題,而其本性卻隱含著無窮。
Mathematics has been called the science of the infinite.
Indeed, the mathematician invents finite constructions by which questions are decided that by their very nature refer to the infinite.
外爾的第一句話,我們已經理解,第二句話也很重要,可是該如何理解呢?
讓我們以【幾何原本】為例:
圖片出處:Mathematical Treasures - Christopher Clavius's Edition of Euclid's Elements
古希臘數學家歐幾裏得的【幾何原本】,是數學史上最重要的文獻之一,這本書的第一句話就暗含了無窮。
定義1. 點:點無法再分割成部份。Definition 1. A point is that which has no part.
有沒有意識到,這個定義很古怪,但是哪裏古怪,又說不出來。
其實,這是歐幾裏得在用精巧的話術,想方設法的要繞開無窮,只是為了說明「點」只有位置,而沒有大小。
如果直接說「點」沒有大小,就必須引出「無窮小」這個至關重要的概念。所謂「無窮小」是指無限的接近於零,卻不等於零。
古希臘人發現「無窮小」會引發很多悖論,他們無法解決,所以只好用「分割」來定義「點」,回避「無窮小」悖論。
如果有人問:你這個定義是不是包含了無窮小?!
那就可以反駁:誰說無窮小了?我說的是「不能再分割」。
不管怎麽說,無窮隱含其中。
有趣的是,無窮小悖論要等到2000多年後才得到解決,方法之一也是「分割」。這裏有很多有趣的故事,將來有機會再詳細展開深談。
另外,這種沒有大小的「點」,是人類頭腦中 想象 出來的。不僅古希臘人從來沒有在自然中發現過,就是我們現代人也沒有見過。
幾何中的「點」是一種超越自然的事物,是歐幾裏得在另一位古希臘哲學家——德謨克利特——發明的原子論的基礎之上,創造出來的數學概念。

定義完了「點」,緊接著,歐幾裏得又在「點」的定義基礎之上,構造出了「線」的定義,
定義2.線:線是沒有寬度的長度。定義3.線的兩端是 點 。
定義4.直線:直線是線上的 點 均勻平直的分布。
Definition 2. A line is breadthless length.
Definition 3. The ends of a line are points.
Definition 4. A straight line is a line which lies evenly with the points on itself.
有了「線」的定義,接下來是「面」的定義,然後是各種「幾何圖形」的定義,……
歐幾裏得構造了點、線、面、形、角等23個數學元素的定義(後面的12卷又增加到了131個),以及5條公理、5條公設,並以這些 有限的 元素和規則證明了465個命題,構建出 無限的 歐幾裏得幾何空間。

圖片出處:Making of Byrne’s Euclid
數學的定義裏有無窮、定理裏也有無窮、數學的空間也是無窮的……,總之數學世界中到處都是無窮。
回過頭來,再重新品味外爾的話
的確,數學家發明了有限構造,透過該構造可以解決問題,而其本性卻隱含著無窮。是不是容易理解了?
數學來源於自然,卻高於自然。
人類觀察鳥的飛行, 發現 了飛行的原理,然後 發明 出飛機這種全新的事物。隨著人類對飛機的不斷改良,飛機的速度和範圍很快就超越了所有鳥類。

同樣的,數學中的元素和規則也是人類觀察自然, 發現 了自然中的規律,然後 重新發明 出來的新事物,這些新事物在自然宇宙中並不存在。隨著幾千年來,數學家的不斷構造和完善,數學宇宙的邊界早已經超越了自然宇宙的邊界。
所以, 數學並不是自然的一部份 ,而是在自然之外的另一套 新事物 重新組成的集合,數學已經自成體系,超越了自然宇宙 。
正是因為人類發明了無窮,發明了數學符號和運算規則,所以數學宇宙的空間 遠遠大於 人類所生活的這個自然宇宙。
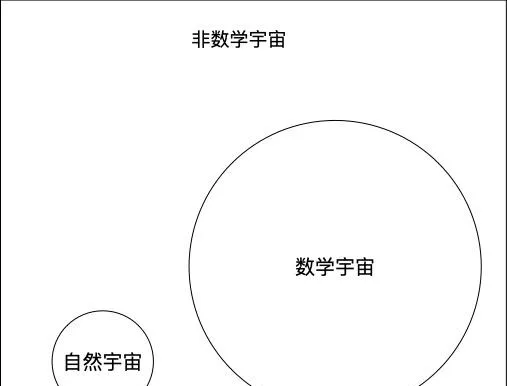
註意,這個圖只是演示數學 可計算的空間 遠遠超出了自然宇宙的範圍,並不代表數學已經比自然大。
數學完全有能力來描述我們所在的這個自然宇宙,但是反過來,數學宇宙中的很多東西是無法用自然事物來描述的,比如無窮。
這是不是很神奇?
愛因斯坦也這樣認為,他說[6]
宇宙的可理解性是宇宙永遠的秘密......宇宙居然能被理解,這個事實本身,就是一個奇跡。The eternal mystery of the world is its comprehensibility … The fact that it is comprehensible is a miracle.
而我們之所以可以理解宇宙,必須要歸功於數學。
20多萬年前,當智人出現在非洲大陸時,此時的智人大腦已經和現代人相差無幾,但那個時候的人類根本無法理解宇宙。
此後的20萬年裏,絕大多數時間,人類也無法理解宇宙。
直到最近的500年,直到人類發明了代數、微積分等現代數學,我們才算真的理解宇宙。
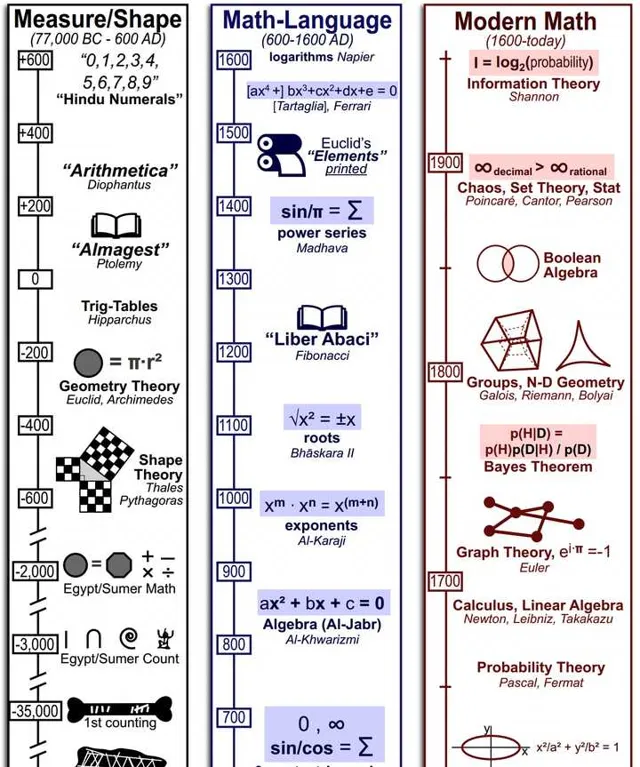
圖片出處:https://www. practicallyscience.com/ a-history-of-math/
按照數學史的時間線:
- 5000多年前,人類發明出算數計算
- 2000多年前,古希臘人發明了幾何證明
- 400多年前,歐洲人發明了代數和微積分
- 100多年前,數學家建立起了現代數學體系
直到此時,愛因斯坦才有能力用現代數學的強大工具發明出了相對論,如果沒有現代數學,即使愛因斯坦也寸步難行。

這個圖片是搞笑用的,但內容是認真的,是數學讓愛因斯坦強大,而不是大家津津樂道的智商和天賦。
一個不會現代數學的愛因斯坦,和一個掌握現代數學的愛因斯坦,只有後者才可以發明相對論。
智商決定不了人的上限,是人所能掌握的數學水平,限制了人能掌握的科學和技術水平,而這些才決定了人的上限。
事實上,數學家每發明創造出一個新的數學概念,都會讓數學的邊界擴充套件出一個更龐大的無窮空間。
如果只依靠發現的話,數學家的能力就會受到極大的限制。
2000多年前,畢達哥拉斯學派的希帕索斯,基於勾股定理 發明 出了根號2,這種不能用自然數的比例(ratio)來表示的 非比例數 (irrational numbers),也就是無理數。
學派認為他發明出的新數,不是自然宇宙中存在的數,是褻瀆神靈的行為,於是淹死了希帕索斯。
如果數學家停止腳步,只使用自然數,而不使用發明出來的新數,那就極大約束他們的能力,就不會有後來高度繁榮的數學世界了。
經過2000多年創造,數學家打破了自然的限制,發明出了越來越多自然宇宙中並不存在的新數。
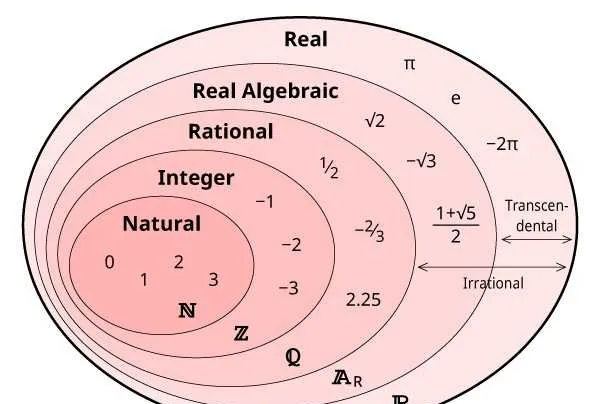
圖片出處:Number Sets
而現代人正是使用負數、無理數、虛數(imaginary number)……等這些數學家發明的數學概念,才能讓我們計算的邊界遠遠超出古希臘人的想象。
到目前為止,我們討論的還只是數學在尺度上的無窮,不要忘了,數學還可以讓維度無窮。
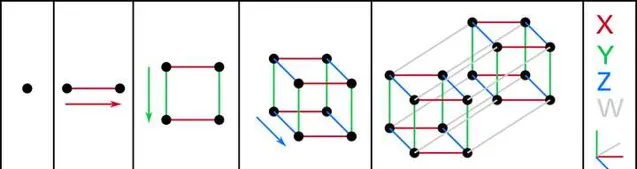
圖片出處:https:// en.wikipedia.org/wiki/T esseract
我們的自然宇宙,是三維空間,再加上一維時間所構成的 四維時空 。
然而,數學家卻可以創造出五維、六維……以至於 無窮維度 的,任意高維的空間,這些發明出來的高維空間在自然中當然也是不存在的。
物理學家費曼就有個【數學和物理關系】的演講,說的就是數學家總是把定理推廣到無窮維空間,而物理學家卻只需要三維空間,非常的搞笑,推薦你看一下[6]。

自然宇宙是一個空間有限、維度有限的宇宙;而數學則可以創造出空間無限、維度無限的宇宙,這些宇宙的數量也可以是無窮多個。
在【三體】中,歌者用二向箔把太陽系碾壓成低維空間,以降維打擊徹底淪陷了地球文明,這是高級文明對低階文明的強大優勢。

圖片出處: 【三體藝術插畫集】
而如果能讓數學家把數學工具帶到自然宇宙的話,他們完全可以碾壓歌者,徹底摧毀歌者文明。
如果想限制住數學家的力量,就讓他們只能用在自然中才存在的事物。
這樣人類的科學探索能力,就會被永遠鎖死在2000多年前的古代,這比智子鎖死基礎物理還要狠毒!(三體迷都知道的梗^_^)
幸好,數學家已經擺脫了自然的限制,就像【西遊記】裏的孫悟空一樣,『跳出三界外,不在五行中』,這是前所未有的自由。『人定勝天』這個夢想,至少在數學上已經完全實作了!
現在你已經明白了,數學的強大力量恰恰來自於發明,而沒有停留在發現上。
數學是人類文明對自然的偉大超越!
數學不是自然科學,而是形式科學
數學超越了自然,也超越了以自然為研究物件的自然科學,所以 數學不是自然科學。
物理學、化學、生物學這些自然科學,他們的所有概念都來自於自然宇宙,不能超越自然宇宙。
而數學中卻有很多超越自然宇宙的事物,例如無窮等。
另外,我們也知道 數學是科學 ,因為數學和其他科學一樣,能提供 確定性 ,是可重復的、可驗證的。
例如,同一個定理,所有人都可以重復驗證其證明過程,得出相同的結論。
所以,我們把數學這種類別的科學歸類於 形式科學 (Formal science)。
這張圖就展示了形式科學和自然科學、社會科學等其他科學的關系。
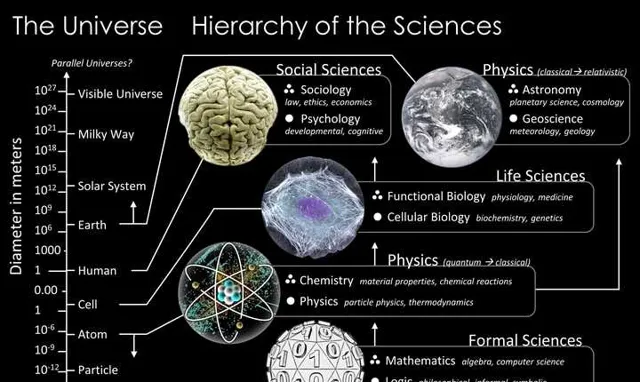
圖片出處:https:// en.wikipedia.org/wiki/H ierarchy_of_the_sciences
從圖中,你可以看到,形式科學雖然不屬於自然宇宙的範疇,卻處於所有科學的最底層。
數學為物理學和化學等提供了堅實的基礎,而物理學和化學又為生命科學提供了的基礎,最後生命科學又為社會科學提供了基礎,這是一個自下而上的層級結構
在拉斐爾的【雅典學院】中,如果仔細觀察就會發現畫中暗藏著一個金字塔形的階層。
整個【雅典學院】以柏拉圖和亞里士多德為中心,同時他們也是身邊人物的視線焦點。
如果以亞里士多德伸出的右手作為頂點,可以做出一個等腰三角形,從台階之上向下延伸到地板,底邊的兩個角右邊指向畢達哥拉斯,左邊指向歐幾裏得。

註意觀察,就會發現這兩個數學家也是周圍人物的視線焦點。
拉斐爾用這樣的構圖來表達,在自然哲學的層級結構中, 數學是整個自然哲學的基礎 。
在【雅典學院】這幅畫裏,拉斐爾還有很多有趣的心機,將來再給大家逐一揭秘。
可是以數學為代表的形式科學為什麽能夠成為自然科學、社會科學的基礎呢?
回答這個問題,就必須理解形式科學是什麽?
什麽是形式科學?
更關鍵的是,什麽是 形式(Form) ?
如果你去搜尋和查閱,就會發現很多類似於形式邏輯、形式語言、形式系統……等各種不明覺厲的抽象概念。
比如維基百科對「形式」的解釋:[7]
形式 (英語:Form)是一個在古希臘哲學中的重要概念。其與質料相對應,描述了事物的本質,指「第一實體」。看完是不是仍然一頭霧水,形式到底是個啥啊!?
可繼續寫下去,就超越了本文的主題,篇幅太長也不利於閱讀。
我會再寫一系列的文章,用通俗易懂的語言,讓大家理解形式科學,同時也解答本文中沒有回答的問題:
我都會在以後的文章中回答。
敬請關註!
總結
本文是從拉斐爾的名畫【雅典學院】開始的,所以也用這幅畫來結束。
在【雅典學院】壁畫的中央,站立著柏拉圖和亞里士多德。

右邊是由達芬奇Cosplay的柏拉圖,他的右手豎著中指(啊不,是食指)指向天空,左手夾著【蒂邁歐篇】,象征著「 形式」 可以構造出理想的世界。
左邊是亞裏斯多德(可能是米開朗基羅Cosplay),右手拍向大地,左手扶著【倫理學】,象征著「 經驗」 需要透過腳踏實地的觀察才能發現。
他們兩個人,正好代表了人類獲得知識的兩種途徑:
一種來自演繹、發明,另一種則來自歸納、發現。
我們都知道,兩者不是非此即彼的關系,而是兼而有之的關系。
但本文的主題『數學是人類的發明,還是發現?』,卻讓人不由自主的想做「二選一」,這是「二元論」的天然特性。至於為什麽人類會有這種傾向,也是一個好問題,我們在下次講形式科學的時候會分析。
警惕「二元論」的陷阱
「二元論」會讓人的註意力頻寬變窄。
如果有人問你:
你想喝咖啡,還是喝茶?
大部份人的註意力都會集中這兩個選擇上,在「咖啡」和「茶」中二選一。

但少數人會註意到,我們其實有無窮種選擇。
再比如:
人是「孩子」,還是「成人」?
小時候是孩子,長大了就是成人,「孩子」和「成人」也不是非此即彼的關系,只是代表了同一個事物、不同的階段。
對數學也是同樣如此,發現和發明也是數學的不同階段:
- 數學家觀察自然,在數量和圖形中發現了數學規律
- 數學家根據發現,設計出新的數學元素,並透過演繹引入了無窮
- 無窮將自然定律變成了數學定理,數學逐漸開始超越自然
- 數學家發明出大量新的數學元素和規則,開拓出一個又一個的數學無窮宇宙
- 人類借助數學宇宙中超越自然的力量,實作了科學、技術的大繁榮
- 數學起源於自然,獨立於自然,超越了自然,最終演化為一個全新的世界
所以,發明和發現在過程上是統一的,並非對立。

你看漫畫裏的這個人,是不是成功跳出了二元論,思維更自由了!^_^
開個玩笑。
解決問題時,更好的技巧是對復雜的事物推遲使用二元論,盡可能多的使用拆解和分析,慢慢的,真相就能浮出水面。這種方法也是所有科學最重要的方法之一,將來一定要展開了介紹。
如果用一句話來總結這篇文章的意義,那就是:
把數學從自然中分割出來,變成了一個獨立的世界。
以前我們總是將兩者混在一起討論,造成了各種混亂,分離之後就清晰多了。
在後面我們介紹形式科學的時候,你會發現這樣分割的巨大好處。
在本文的開頭,我提到過,對這個問題感興趣,還點進來看的人,都不是一般人。
而能堅持到這裏的人,我相信更是寥寥無幾。
別忘了給自己,也給這個答案點個贊,留作紀念!
One More Thing:
這篇文章和接下來的系列文章,都會在我的微信公號上釋出,最後將集結成冊,組譯為一本迷你電子書,供大家免費下載,書名暫定為【形式宇宙】。
敬請關註我的微信公號: zyfedu
最後,給大家分享一本數學電子書。
關註我的微信公號zyfedu,在私信中發送:幾何原本
就可以獲得文章中提到的最美彩版【幾何原本】的PDF電子版。
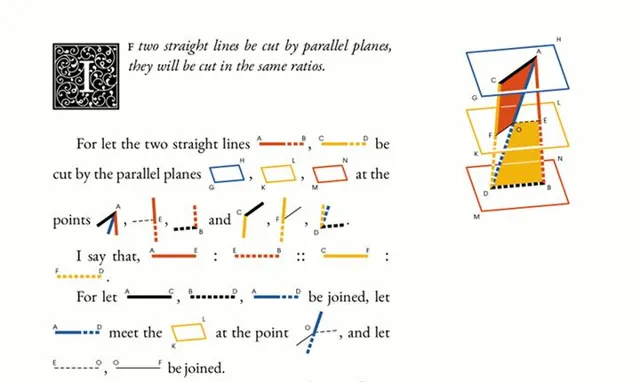
1847年,愛爾蘭工程師Oliver Byrne出版了一套非常驚艷的【幾何原本】,全書的插圖全部采用彩色印刷,顛覆了傳統幾何書籍灰暗單調的風格。[8]

圖片出處:Making of Byrne’s Euclid
http:// c82.net 網站對該書做了數碼修復,並制作了可互動的線上【幾何原本】,強烈建議大家去體驗一下。
上海三聯書店也出版了該書的紙質版,售價高達400多元,土豪請無視高達二字。我在微訊號zyfedu上分享的PDF檔,是俄羅斯人Sergey Slyusarev用ConTeXt制作的前六卷。[9][10]
該電子書的特許協議是CC-BY-SA 4.0 ,你也可以在Github上找到該書的ConTeXt原始碼
以後我還會分享更多的公版科技圖書給大家,敬請關註。
關於本文的分享和轉載須知
歡迎個人分享和轉發本文連結,你的點贊和分享對我很重要!
媒體、自媒體轉載,請獲得本人授權,註明作者和出處。
參考資料
- https:// en.wikipedia.org/wiki/O bservable_universe
- 洪萬生教授的講座【數學是發現,還是發明?】影片 https://www. youtube.com/watch? v=brGqGEBnqyc&t=4984s ,文字稿【探索10 】數學是發現,還是發明?
- Weyl, H. Axiomatic versus constructive procedures in mathematics. The Mathematical Intelligencer 7, 10–17 (1985). https:// doi.org/10.1007/BF03024 481
- Albert Einstein(1923). "Geometry and Experience". Sidelights on relativity . Courier Dover Publications. p. 27.Reprinted by Dover (2010), ISBN978-0-486-24511-9.
- Andrew Robinson. Did Einstein really say that? Nature 557 , 30 (2018). https:// doi.org/10.1038/d41586- 018-05004-4
- 【費曼物理學2-5】費曼趣談數學家與物理學家的區別_嗶哩嗶哩 (゜-゜)つロ 幹杯~-bilibili
- https:// zh.wikipedia.org/wiki/% E5%BD%A2式_(哲學)
- https:// en.wikipedia.org/wiki/O liver_Byrne_(mathematician)
- https:// habr.com/ru/post/451682 /
- 我如何用TeX「復活」兩千多年前的【幾何原本】? - 雲+社區 - 騰訊雲










