有趣的題目。在計算之前,我們先了解下馬利安納海溝的一些數據。
馬利安納海溝,位於太平洋西部地區馬利安納群島東南部。 其最深點距離海面以下約 11,034 米, 這使得它成為地球海底已知的最深點。

馬利安納海溝是由於太平洋板塊和菲律賓板塊相互碰撞而形成的,具體說是:太平洋板塊俯沖在較小、密度較低的菲律賓板塊下方形成的, 這種碰撞導致了地殼的下沈,形成了深海槽。如下圖紅框。

好了,下面我們回答三個問題。
問題一:鋼球沈入海底後會因為高壓破裂嗎?
當鋼球下沈並到達海溝底部時,它將受到水的極大壓力。那這個壓力是否會破壞鋼球?水在這個海底,約11千米,施加的壓強可以透過公式計算:
P = ρgh = 1.134×10^8 (Pa)
其中:P = 壓強(帕斯卡),ρ = 水的密度(1050千克/立方米,深海處的水密度略高於海面),g = 重力加速度(9.81米/秒²),h = 深度(11千米)。要判斷鋼球的狀態,我們要知道屈服強度(見參考資訊【1】),它是指施加在材料上使其永久變形的最小應力。鋼球的屈服強度,是250MPa,基本是水底壓強的兩倍多。另外,鋼球的Hugoniot彈性極限(衡量材料能夠承受的最大應力值【2】)約為10^9Pa,也大於水壓。因此, 鋼球到底海溝地步,水的壓強不足以導致鋼球永久變形或者破裂,即鋼球都將保持其形狀和結構。
然後, 水底壓力將擠壓鋼球並減小它的體積。我們鋼的體積彈性模量(B)來計算這一點【3】。體積彈性模量 = 施加的壓力 / 體積的變化比例,用公式表示為:P = −B(V − V0)/V0,其中P是將一定質素的材料的初始體積V0減小到V時產生的壓力。

我們知道馬利安納海溝底部的壓力差ΔP,以及鋼的體積彈性模量。如果我們假設球的體積為 1.0 m^3。 我們可以計算由於壓力差ΔV而導致的鋼球體積變化如下:
ΔV = VP / B = 0.000709 m^3
再來看溫度,假設馬利安納海溝上方海面的水溫約為24°C,而底部約為4°C,溫差為20°C也將導致球的收縮,但這不會影響球內的應力。由於溫度差異ΔT,可以使用以下公式計算體積減小 \Delta V_{t} :
\frac{\Delta V_{t}}{V}=\alpha\Delta T
其中:
V = 1立方米(鋼球的初始體積), \alpha = 36×10^-6°C^-1(鋼球的體積熱膨脹系數),ΔT = 20°C(溫度差異)。因此, {\Delta V_{t}} = 0.00072m^3。所以, 海底壓力和溫度差異一共導致鋼球體積減少0.001429立方米,也就是減少了0.1429%。換算成半徑,球的減小後半徑將為0.620055米(原始半徑0.6203505米)。
由於海底壓力小於屈服強度,所以這樣的 形變是彈性的,即如果球被帶回到地表,它將恢復其原始體積。
問題二:鋼球需要多久可以到達海底?
回答這個問題,我們需要知道 終端速度 (terminal velocity,詳見參考資訊【4】),其定義為物體落入流體中所達到的最高速度,即當阻力和浮力之和等於作用在物體上的向下重力時,所獲的的速度:
v_{t}=\sqrt{\frac{2mg}{\rho A Cd}}
v_{t} 是終端速度,m是下落物體的質素 6750kg ,g是重力加速度 9.8,Cd是阻力系數 0.47,ρ是流體密度 1000 kg/m^{3} ,A是物體投射的面積 1.209 m^{2} ,代入得到: v_{t} =15.3m/s。
所以,鋼球將在12分鐘左右到達馬利安納海溝底部(11km)。
問題三:沈入海底的鋼球會被海水腐蝕,多久會腐蝕完?
海水裏含鹽分,所以,沈入海底的鋼球會被海水腐蝕。
鋼材的腐蝕取決於水中溶解氧的量。 下圖為北太平洋溶解氧垂直分布圖,可以直觀地表示氧氣在海洋中的垂直分布情況。溶解氧量在深度超過 5000 米時保持恒定【8】,包括馬利安納海溝底部。海水鹽度大概在3000米以下變動很小。
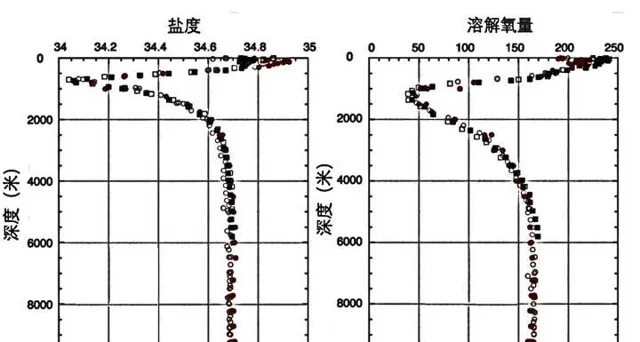
根據參考資訊【6】的數據,鋼鐵在海中5100m的腐蝕速率為每年0.06毫米。考慮到溶解氧量在較大深度是恒定的,而且在海水中無法形成持久的保護層來保護鋼材免受腐蝕,我們可以將用恒定的腐蝕速率來計算馬利安納海溝底部鋼球的腐蝕。
因此,我們對半徑為0.620055米的鋼球的腐蝕進行如下計算:
鋼球完全腐蝕所需時間 = 62.0055 / 0.06 = 10334.2年。
所以,如果鋼球靜止不動,大概會在10334年以後,被完全腐蝕掉。
但是,板塊是運動的,比如太平洋板塊向歐亞板塊方向的移動速率大概是每年7到14厘米【9】,一萬年以後,大概會移動一公裏左右;也就是說,如果鋼球隨著板塊移動,那麽 在鋼球被完全腐蝕之前,它會被下侵的太平洋板塊帶入到地殼內部。 如果不考慮地層壓力,這樣的缺氧環境會延緩腐蝕,鋼球存在的時間會遠超上述腐蝕時間,最終可能會隨著板塊進一步的下沈,在深部的高溫高壓下融入為上地幔的一部份。或者,在強大的地層壓力下,鋼球受變質作用影響,融為地殼的一部份。
謝謝閱讀和點贊。
參考資訊:
1 Yield Strength - Meaning, Features, and FAQs (vedantu.com)
2 The Hugoniot elastic limit
3 Bulk modulus | Physics, Elasticity, Compressibility | Britannica
4 Terminal Velocity Derivation With Simple Step By Step Explanation (byjus.com)
5 Geo explainer: Exploring the Mariana Trench - Geographical
6 (PDF) Corrosion of ferrous alloys in deep sea environments (researchgate.net)
7 Genomic Potential in Hydrothermal Vents | News | Astrobiology (nasa.gov)
8 Chemical characteristics of hadal waters in the Izu-Ogasawara Trench of the western Pacific Ocean - PMC (nih.gov)
9 Plate Tectonics
| Pacific Northwest Seismic Network .
10. Marianas Trench
9.12
謝謝大家的閱讀和點贊。看到很多有用的評論,都更好地完善了上面的回答,在此一並謝過。
如評論區所說,鋼球的腐蝕是一個復雜的過程,比如大家提到的 腐蝕的速率隨時間不是線性的 ,而且 隨著腐蝕,鋼球的體積變小會反過來影響壓強的變化 ,以及 水的密度隨深度變化不是常數 等。都是很切合實際的建議。本回答中的公式是一個線性的常數模型,更多的是想給大家一個思路,供探討。的確上面提到的這些建議,理論上,都會使得最終的預測時間更準確,也值得感興趣的人進一步推導。
說到這裏,我最後分享一個工作中一個小小的體會:很多建模或者預測問題,實際運用中最robust的方法反而是比較簡單的方法;而很多復雜的模型,因為參數多,且參數難以估計,往往實操中表現不盡如人意。
9.13
評論區很多問 海底的水密度 。 表層海水的密度約為 1020 到1029 kg/m3,具體取決於溫度和鹽度 ,給一個具體的數據,當海水溫度25℃、鹽度35g/kg、1個標準大氣壓,海水的密度為1023.6kg/m3。 在海洋深處的高壓下,海水的密度可以達到1050kg/m3或更高一點 。所以,深海的海水密度的確會高,但是與海面比,密度不會相差很大。大概就是1020 和1050的區別。
9.17
評論區有問屈服應力。屈服應力或者屈服強度,是金屬材料發生屈服現象時的極限應力,也就是可恢復的彈性變形和永久塑形變形的界限。小於屈服強度,變形可恢復。大於屈服強度,則變形不可恢復。這個概念在工程建築中十分常見,即要求工程受力在彈性可恢復的範圍內,小於屈服強度。










