如果是纯数学天赋.
无疑目前已知最有数学纯天赋的就是这一位.

印度的拉马努金,虽然拉马努金成就没有顶尖王者高斯或者欧拉大,但个人认为纯天赋,他无疑是神,最主要体现在他, 完全凭借着直觉 ,缔造了两三千个超前理论公式,却不知道怎么去证明,可见他完全是天选之子,他和其他的数学家思维不一样,通常讲,数学是理性且逻辑非常突出的一类学科,其他数学家,基本上都是具有非常强大的逻辑思考的,偏向于证明,而他给人感觉就是靠直觉来判断.
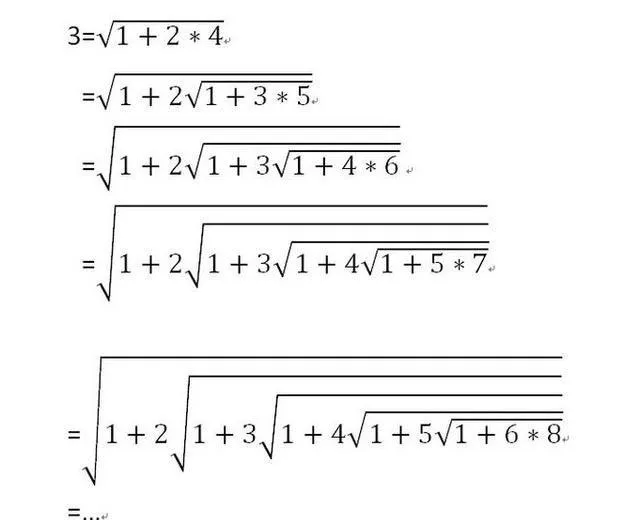
这里的纯数学天赋,就是拥有这样极其敏感的直觉能力,拥有极强的创造力,尤其是在高等数学之中,越高阶越依靠于灵感缔造,这样也是符合人类大脑结构的,我们面对数学难题,要么就是凭脑海回忆知识链熟悉的技巧性,要么就是突然灵机一动,并没有那种书本给人的逻辑性,牛顿微积分的缔造,当时也没有完全证明,给他擦屁股的是柯西魏尔斯特拉斯这样数学家,注意,我们今天的高数是先读了极限论再学的微分学,从而循序渐进的,可是牛顿当时并没有极限论,包括欧拉的欧拉公式,在当年复变函数未成型之前,他是怎么思考的欧拉公式,已不得而知.
如果说逻辑才是数学的王道,那么计算机早已统治全世界了——灵性的力量.
当然,最佩服的数学家无疑是高斯,是我内心中最具有数学天赋的孩子.
因为喜欢他的传奇性:
9岁时,发现了高斯求和,即算数级数(等差数列)的求和方法,面对老师的刁难,他用很短的时间计算出了小学老师布置的任务,似乎就是影视剧中的奇才,从1+2+3+4+5+……+100的求和,他所使用的方法是(1+100)+(2+99)+(3+98)+,得……到了结果:5050.

12岁时,已经开始怀疑元素几何学中的基础证明.
16岁时,预测在欧氏几何之外必然会产生一门完全不同的几何学,即非欧几里得几何学。他导出了二项式定理的一般形式,将其成功的运用在无穷级数,并发展了数学分析的理论。

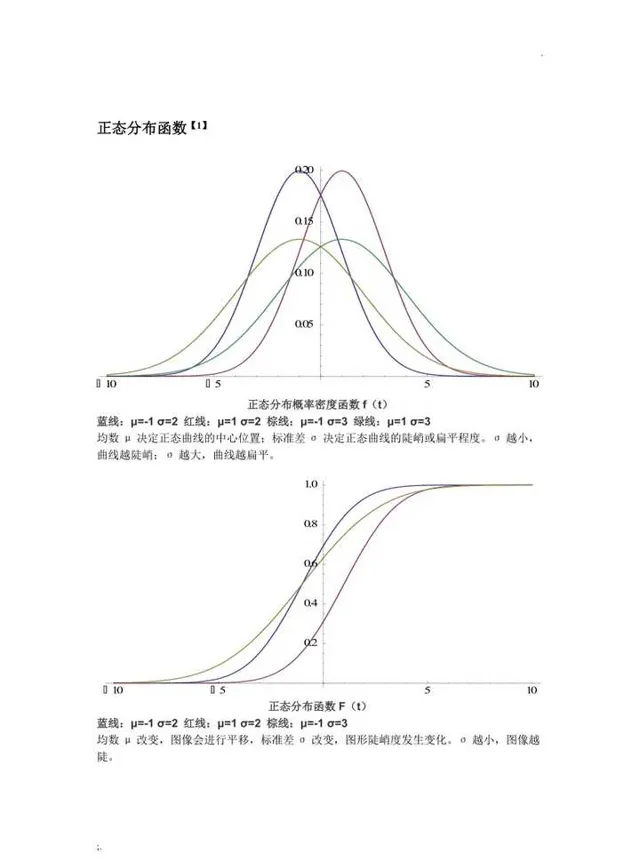
17岁时,发现了质数分布定理和最小二乘法。通过对足够多的测量数据的处理后,并得到高斯正态分布曲线,其函数被命名为标准正态分布,或高斯分布,并在概率计算中大量使用。
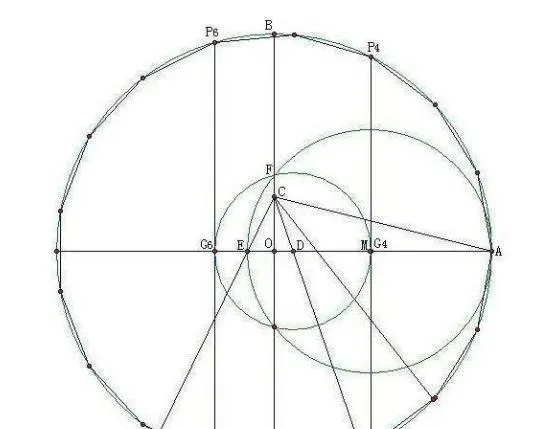
18岁时,一夜之间解决了千年数学难题,连阿基米德,柏拉图,牛顿……千年内等顶尖大神都束手无策的正十七边形尺规作图法,而当时,那仅仅是他的老师和他开的一个玩笑,对于他那仅仅只是个家庭作业.
……
好了主要是书写童年和少年的高斯.










