CAE工程师一名,最近在复习材料力学,正好回答这个问题。
高赞的各位写得都很专业,但个人认为 @蒙特遇见卡罗 的观点最为简单明了。
若弹性模量影响系统刚度分配,则应力结果与弹性模量有关,比如超静定问题;若弹性模量不影响系统刚度分析,则应力结果与弹性模量无关,比如单个试件单轴拉伸实验。
我们首先来看拉压、弯曲、扭转和组合工况中,应力与弹性模量是否有关。
1、哪些情况应力与弹性模量无关?
1.1 单轴拉伸工况
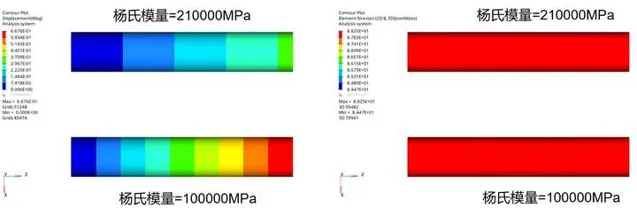
单轴拉伸工况,两个试件左端固定约束,右端施加相同大小的力使试件产生拉伸变形,弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量不同,但应力完全相同 。
单轴拉伸时,应力计算公式为 \sigma=\frac{F}{A} ,F为拉力,A为截面积,应力与弹性模量完全无关。

1.2 弯曲工况
弯曲工况中,两个试件左端固定约束,右端施加相同大小的力使试件产生弯曲变形,两个试件弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量不同,但应力完全相同 。
纯弯曲时,梁截面上正应力计算公式为 \sigma=\frac{My}{I_z}=\frac{My}{\int_{}^{}y^2dA} , M 弯矩,y为与中性面距离,A为面积,应力与弹性模量完全无关。

1.3 扭转工况
扭转工况,两个试件左端固定约束,右端施加相同大小的扭矩使试件发生扭转变形,两个试件弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量不同,但应力完全相同 。
纯弯曲时,圆柱截面上切应力计算公式为 \tau_{max}=\frac{TR}{I_p}=\frac{TR}{\int_{A}^{}\rho^2dA} ,T为扭矩,R为圆柱半径,应力与弹性模量完全无关。
1.4 组合变形工况
拉伸+弯曲+扭转组合工况下,两个试件,左端固定约束,右端施加相同大小的扭矩+拉力+弯力使试件发生组合变形,两个试件弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量不同,但应力完全相同 。
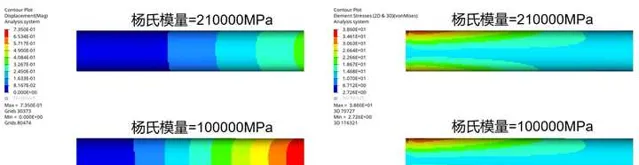
由以上内容可知,对于单个零件而言,拉伸、弯曲、扭转以及组合工况下,应力结果与弹性模量无关。
2、哪些情况应力与弹性模量有关?
2.1 位移加载
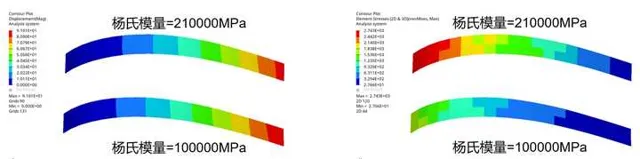
单轴拉伸工况,两个试件左端固定约束,右端施加相同大小的强制位移载荷,两个试件弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量相同,但应力不同,此时应力与弹性模量有关 。

2.2 大变形工况
大变形工况下,两个试件左端固定约束,右端施加相同大小的集中力载荷,两个试件弹性模量分别取210GPa和100GPa,由下图可知,两个试件 变形量不同,应力也不同,此时应力与弹性模量有关。
2.3 超静定问题
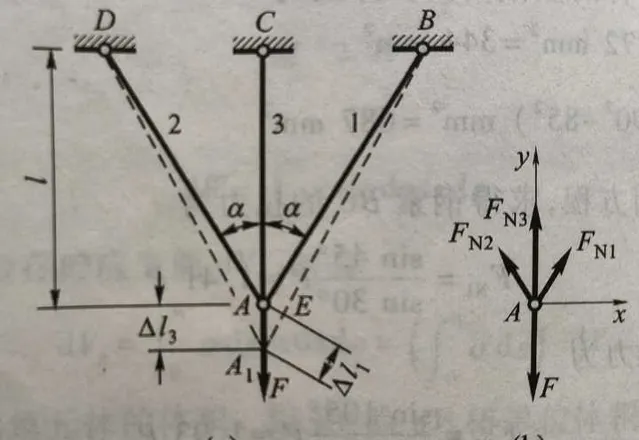
如下所示超静定问题,杆1、杆2和杆3为材料相同半径相同的圆杆,加入变形协调方程可求得杆1、杆2和杆3的受力大小分别为 F_{N1}=F_{N2}=\frac{Fcos^2\alpha}{2cos^2\alpha+\frac{E_3A_3}{E_1A_1}} , F_{N3}=\frac{F}{1+2\frac{E_1A_1}{E_3A_3}cos^3\alpha} 。
轴力不同,根据 \sigma=\frac{F}{A} 可知,三根杆上应力也不同,此时弹性模量会影响系统刚度分布,从而影响载荷分配,最后导致应力不同,此时应力与弹性模量有关。
实际工程应用中,多数结构都是越静定结构,其载荷分配都与弹性模量有关,因此多数实际结构中,应力结果都与弹性模量有关。
结论如下:
装配体中,弹性模量影响系统中刚度分配,刚度分配决定传递载荷大小,载荷大小影响应力;
若弹性模量不影响系统中各零件的刚度比值,则弹性模量不影响应力大小,比如材料力学中的单个零件简单的拉压、弯曲、扭转和剪切四种基本变形;
若弹性模量影响系统中每个零件的刚度比值,则弹性模量影响应力大小,比如绝大多数超静定工况。
我的上一篇文章中写到了焊缝/焊点区域应力计算不准确问题,应力不准确的原因可以用上面的结论来解释。
点焊和缝焊过程中,焊接区域的高温会影响周围热影响区的材料性能参数,其弹性模量会发生改变;对于装配体,单个部件某个区域的弹性模量改变会影响整个系统的刚度分配,从而导致整个模型中载荷分配发生变化,最终会导致焊接区和热影响区应力发生改变;
焊接仿真目前最大的问题在于无法获得热影响区准确的材料参数,因此无法得到焊接区域准确的应力分布。
码字不易,点个赞吧,更多有限元相关硬核分享,请点击头像,查看我的主页 @熊库辛












