谢邀。抛块儿砖。
首先回答「除了美观还有什么作用」。
地图既是一种工具也是一种艺术。地图轮廓以及填充、标注的简化(cartographic generalization,感谢 任畅同学的纠正,官方中文翻译叫制图综合)的主要目的,其实已经被题主说到了:准确、简洁、美观。其实还有一个目的,那就是通过减少细节来 突出重点 。
当画幅(比例尺)变化的时候,很多的细节不可能都一一地表现在图上。例如下图(来自加拿大的拉瓦尔大学):
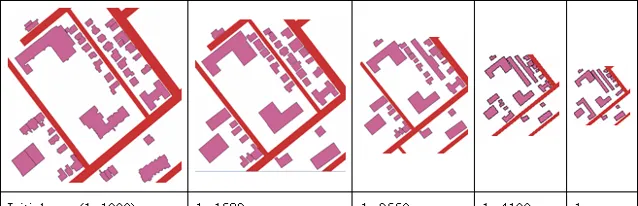
比例尺是1:1000的时候,地图上可以保留很多细节,比如所有的路径,以及各个建筑的轮廓。但是到了1:27176的时候,如果再保留所有路径或建筑的轮廓,那就一团乱麻,什么也看不清了。
有时候,少也是多(Less is more)。只有削去了不重要的枝枝叶叶,主干的信息才能更好地被突出展现出来,地图才能达到它应有的效果。
而且,比例尺并不是地图简化的唯一原因。每一幅地图都有自己的目的。目的不一样,对于各种细节的要求也就不一样。比如网上这张反映一带一路的地图:
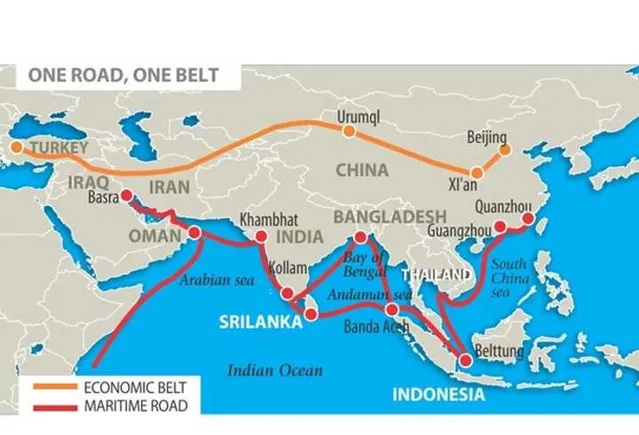
经常看地图册的人一眼就能看出很多「错误」,比如北京的位置貌似偏了些,琼州海峡没了,马尔代夫和琉球也没了,日本那几个岛也连在一起了,等等。但是,这张图的目的是展现一带一路,并不是为了告诉人们马尔代夫在哪里,北京在哪里。弱化了一些细枝末节的东西,则更能强调出一带一路的这个主题。试想一下,如果这张地图把陆地轮廓画得特别详细,还加上中国的省界,甚至长江黄河,那它的主题会不会反而被冲淡了?
接下来就具体回答题主最主要的一个问题:地图的细节是怎样被简化掉的?
从种类上说,map generalization可以分为:

题主在题目补充里谈的是海岸线的简化,也就是地图的线性轮廓(海岸线、国界线、河流、等高线……)的简化,即上面谈到的方式里的Simplified。
绘制轮廓一般用的是矢量数据。所以,这里讨论的地图轮廓简化方法,实际上也是矢量数据的压缩方法。
介绍具体方法以前,先要说一下总体的前提条件。不管多复杂的曲线,我们也认为它是由一个个的线段组成的,而线段的两端都是一个个的数据点。越「圆滑」的轮廓,数据点就越多。
常见的简化方法有这几种:
1. 简单粗暴 - 隔点法
隔点法就是在矢量曲线的一系列点中,每隔n个点选取一个来保留,其余没选中的点都删除。比如说下面这张图的曲线:
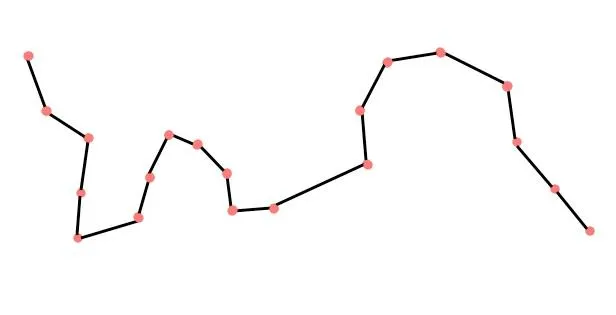
现在我每隔2个点选择一个留下,剩下的点删除,就把这条曲线简化成了紫色的这种样子:
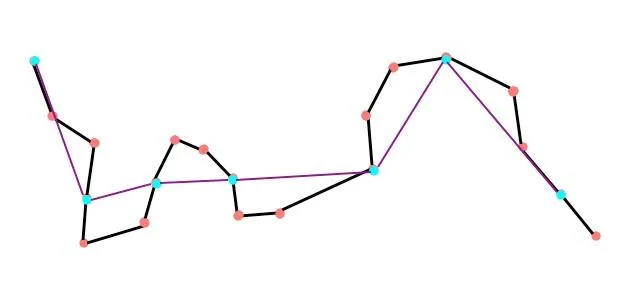
如果我每隔3个点选择一个留下,则简化后的曲线是这个样子的:
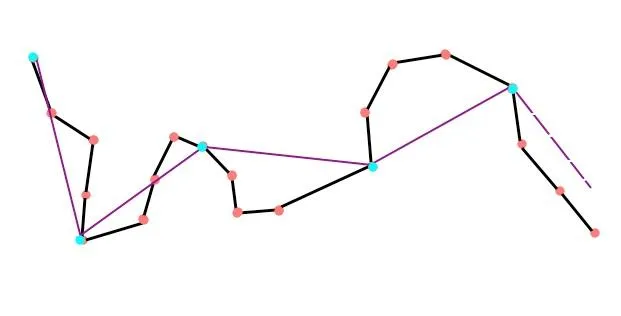
这种做法的优点是算法简单,操作简单,但是缺点是比较重要、有特色的点很可能会被漏掉。在原本的曲线就不那么平滑的情况下,这么做很可能造成比较大的形变。比如地图上的半岛或者海湾,在n选择不当的时候,很可能就直接被切掉了。
2. 步步为营 - 垂距法
这种垂距法是一种比较常用的办法。它是按照某个指定的方向,一步一步地简化曲线。比如下面这张图:
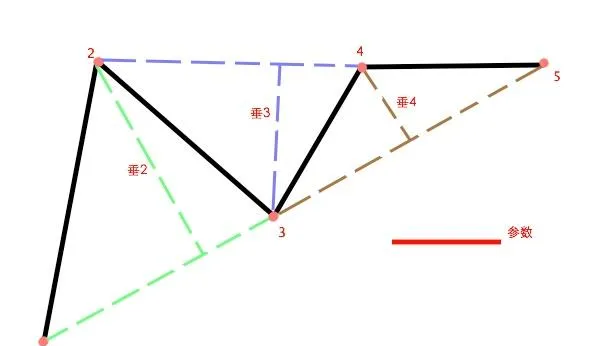
首先我们要指定一个参数长度,比如图中的红色线段。
然后,我决定从左到右地简化这条曲线,因此我首先要选择1、2、3这三个点。
连接1和3,然后通过2作垂线和1、3的连线相交。测量垂2的长度。图中,垂2的长度大于参数,因此要保留点2.
然后挪位到2、3、4这三个点,连接2和4,再画出垂3。比较垂3和参数。这里的垂3还是大于参数,因此点3也保留。
然后挪位到3、4、5这三个点。连接3和5,再作垂4.这里,垂4的长度是小于参数的,因此点4就要被删除掉。
然后继续向右,挪位到3、5、6(4被删除了)等等一直进行下去。
3. 宏观调控 - 分裂法
这种方法还有一种高大上的名字叫做道格拉斯·皮尤克算法,也是一种用得比较多的方法。它和垂距法有相似之处,都是需要设定一个参量来进行比较。但是它们也有很大的不同。比如,垂距法是从左到右(或者从右打左)一步一步地进行曲线简化。而道格拉斯·皮尤克算法则是把整个曲线看做一个整体,来进行「宏观调控」。它的具体操作如下。
比如,现在有这么条曲线:
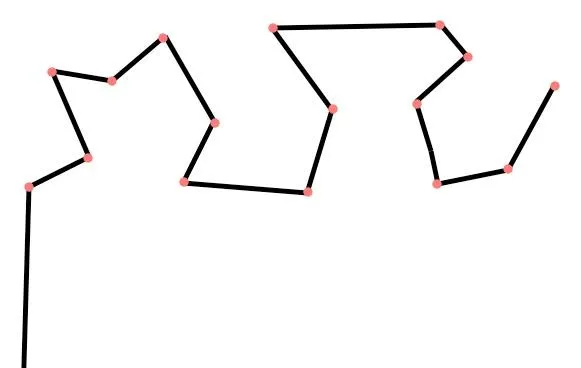
用这种方法,我们就要从整体入手:
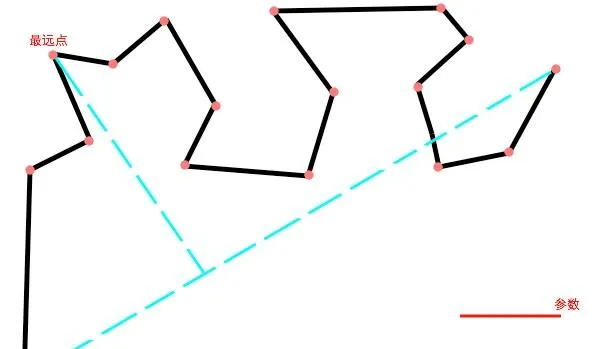
首先要做的就是选参数「红色线段」。然后连接整条曲线的首位两点。连接之后,找出离这条连线距离最远的那个点,比较这个点到连线的距离和所选参数的大小。图中现在的最远点是明显大于参数的,因此这个点被保留。
然后进行下一步:
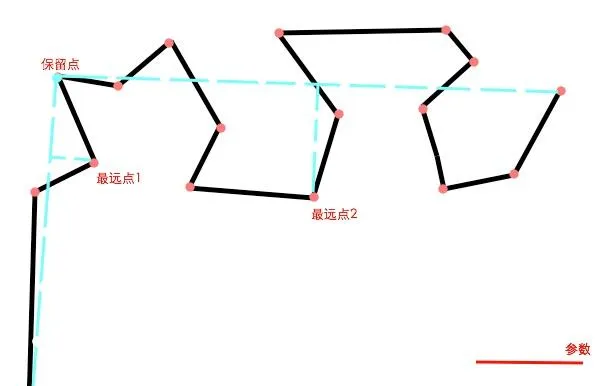
连接起始点和保留点,以及终点和保留点。再分别找出两条连线区间范围内的最远点,并将它们的距离和参数比较。这里,最远点1的距离是小于参数的,因此在这个区间内的所有点都要被删除掉。而最远点2的距离刚好大于参数,因此最远点2也成为了被选取的保留点。
接下来:
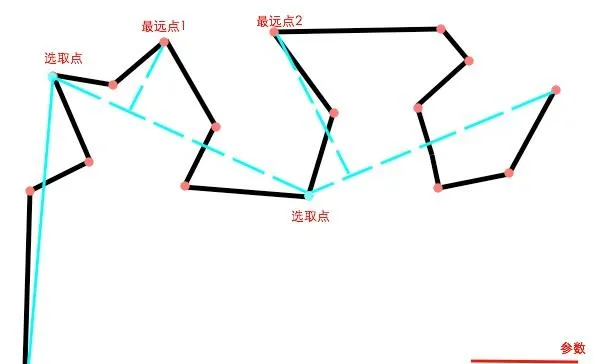
连接上一个保留点和新的保留点,以及新的保留点和终点,同样的道理,分别找出两个区间内的最远点以及距离。这里的最远点1的距离小于参数,因此这一区间的所有点都删除。最远点2的距离大于参数,则成为新的选取点被保留。
同理继续进行筛选:
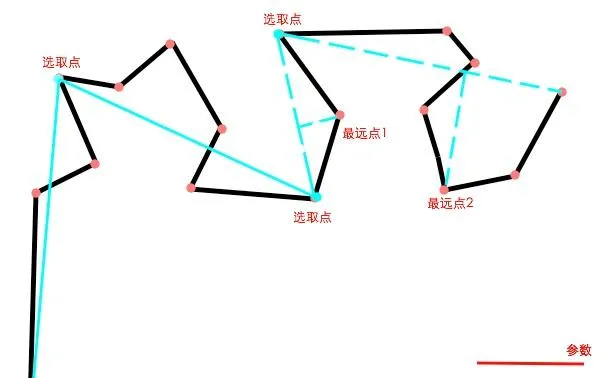
最远点1所在区间的点被删除,最远点2成为新的选取点被保留。
再来一次:

这次最远点1保留,最远点2所在区间的点删除。
再来一次:
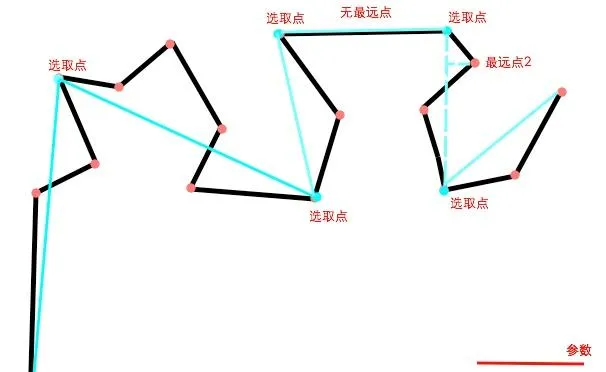
同样的作法。
最后,这条蓝色的曲线就是通过道格拉斯·皮尤克算法简化后的曲线:
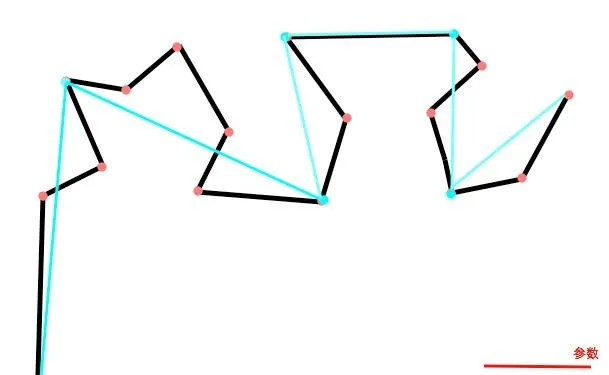
不论是垂距法还是道格拉斯·皮尤克算法,重要的一点都是要选择一个合适的参数。参数越大,地图被简化的程度就越大。
知乎专栏:地球的那些事儿











