LQR(Linear Quadratic Regulator)即线性二次调节器,作为一种最优控制器,通过设计出的状态反馈控制器K使得二次型目标函数J取得最小值,从而达到最优控制的目的。本篇以Apollo源码实例阐述LQR在车辆横向控制中的应用,从仿真到实现分析该算法的控制性能。
代码链接:
对于车辆的横向系统,不难得知基于跟踪误差变量的状态方程模型为:
\scriptsize \frac{d}{dt}\begin{bmatrix}e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & -\frac{C_{af}+C_{ar}}{mV_x} & \frac{C_{af}+C_{ar}}{m} & -\frac{C_{af}l_{f}-C_{ar}l_{r}}{mV_x} \\ 0 & 0 & 0 & 1\\ 0 & -\frac{C_{af}l_{f}-C_{ar}l_r}{I_zV_x} & \frac{C_{af}l_{f}-C_{ar}l_r}{I_z} & -\frac{C_{af}l_{f}^2-C_{ar}l_r^2}{I_zV_x} \end{bmatrix} \begin{bmatrix}e_1 \\ \dot{e_1} \\ e_2 \\ \dot{e_2} \end{bmatrix}
\scriptsize + \begin{bmatrix} 0\\ \frac{C_{af}}{m}\\ 0\\ \frac{C_{af}l_f}{I_z} \end{bmatrix}\sigma + \begin{bmatrix} 0\\ -\frac{2C_{af}l_{f}-2C_{ar}l_r}{mV_x}-V_x\\ 0\\ -\frac{2C_{af}l_{f}^2+2C_{ar}l_r^2}{I_zV_x} \end{bmatrix}\dot{\varphi _{des}}
其中, \scriptsize e_1 为横向偏差, \scriptsize e_2 为航向角偏差,上述模型可参照< 车辆动力学及控制 >第二章;
由此,可将其重写为:
\scriptsize \dot{x} = Ax+Bu+C
由于上述系统为连续系统,还需进行相应的离散化。离散化后,对应的标准形式为:
\scriptsize x(k+1)=A_d*x(k)+B_d*u+C_d
各变量的对应关系如下:
\scriptsize A_d = \frac{e^{\frac{AT}{2}}}{-e^{\frac{AT}{2}}} = \frac{I+\frac{AT}{2}}{I-\frac{AT}{2}} =({I-\frac{AT}{2}})^{-1}(I+\frac{AT}{2})
\scriptsize B_d = \int_{T}^{0}e^{AT}dtB=TB
\scriptsize C_d=TC
目标函数的选择:
\scriptsize J=\sum_{N-1}^{0}(x^TQx+u^TRu)
其中 \scriptsize Q 为状态权重矩阵, \scriptsize R 为控制权重矩阵, \scriptsize x 为状态矩阵, \scriptsize u 为控制矩阵。
基于LQR的横向动力学仿真性能分析
由横向动力学方程可知,不同车速情况下,其动力学表征不同。为分析车速对控制性能的影响,特构建Matlab的性能仿真环境,以此来分析工况的不同对控制性能的影响。
阶跃响应分析:不同车速下,系统的单位阶跃响应曲线如图所示。由图可知,当输入的速度越快时,系统的响应越快。
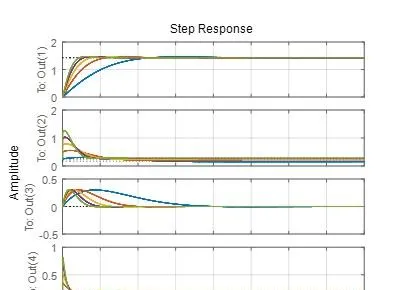
鲁棒性能分析:
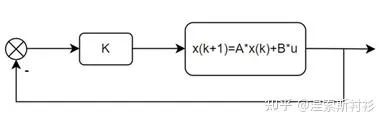
LQR的系统框图可知,横向系统的开环增益函数:
\scriptsize L(s)=K(SI-A)^{-1}B
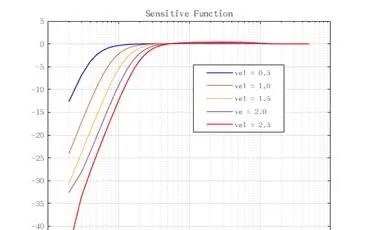
由此,灵敏度函数可写为:
\scriptsize S = \frac{1}{1+L(s)}
由灵敏度函数的响应特性可知,系统在低速状态下的误差抑制性能相对较弱。
为改善系统的响应特性,Apollo还引入了Lead_Lag控制器。当引入Lead_lag控制器后,系统的开环幅频响应特性为:
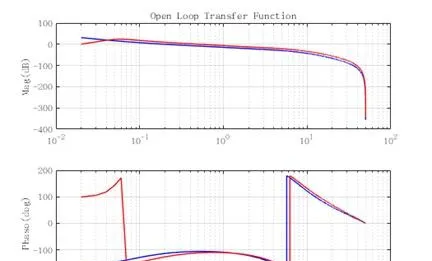
MPC与LQR的比较:
(1) LQR的研究对象是现代控制理论中以状态空间方程形式给出的线性系统,而MPC的研究对象可以是线性系统,也可以是非线性系统。不过对于非线性系统,可以将其线性化处理后进行求解。
(2) 本质上都属于优化问题;
(3) 工作时域的不同,LQR的计算针对同一工作时域,在一个控制周期内,LQR只计算一次,并将此次计算出的最优解下发给控制器即可;而MPC是滚动优化的,计算未来一段时间内,每个采样周期都会经过计算,得出一组控制序列,但是只将第一个控制值下发给控制器.
参考文献
[1] 自动驾驶(七十二)---------LQR控制算法
[2] LQR and MPC
[3] 开发者说 | Apollo控制算法之汽车动力学模型和LQR控制
未完待续











