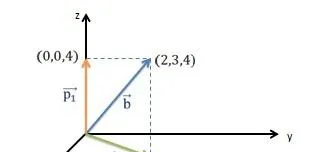
你能求出 \vec{b}=\begin{bmatrix}2\\3\\4\end{bmatrix} 在 z 轴和 xy 平面的投影(projection)吗?分别向 z 轴和 xy 平面做垂线,不难得出 \vec{b} 在 z 轴的投影 p_{1}=\begin{bmatrix}0\\0\\4\end{bmatrix} , \vec{b} 在 xy 平面的投影 p_{2}=\begin{bmatrix}2\\3\\0\end{bmatrix} 。前瞻性的多说一句,因为 z 轴和 xy 平面互为正交补,所以 p_{1} 和 p_{2} 正交,且 p_{1}+p_{2}=\vec{b} 。
投影包含了两层意思:
上面例子的投影空间分别是 z 轴和 xy 平面,它们太特殊,现在我们看看一般情况下如何求投影:
问题一:求 \vec{b} 在直线 \vec{a} 方向的投影。
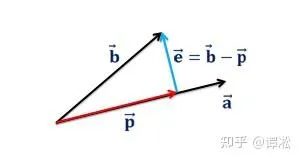
有一条过原点且沿着 \vec{a}=\begin{bmatrix}a_{1}\\a_{2}\\...\\a_{n}\end{bmatrix} 方向的直线,我们要求 \vec{b}=\begin{bmatrix}b_{1}\\b_{2}\\...\\b_{n}\end{bmatrix} 在这条直线的投影 \vec{p} 。因为 \vec{p} 和 \vec{a} 共线,所以 \vec{p}=x\vec{a} 。 求投影的关键就是要利用正交性: \vec{b}-\vec{p} 和 \vec{a} 正交。 \vec{b}-\vec{p} 是原矢量和投影的差,代表误差,通常用字母 \vec{e} 表示。从几何角度我们就可以知道投影意味着 \vec{e} 和 \vec{a} 正交,即 \vec{a}\cdot\vec{e}=0 。根据正交关系立刻可以得出 \vec{a}\cdot (\vec{b}-\vec{p})=0\Rightarrow\vec{a} \cdot (\vec{b}-x\vec{a})=0\Rightarrow x=\frac{\vec{a}\cdot \vec{b}}{\vec{a}\cdot\vec{a}}=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}} ,我们率先求出了系数 x , x 表达式中分子分母是两个点乘,结果都是标量数字,所以 x 也如我们所料是个数字。那么相应的投影 \vec{p}=\frac{\vec{b}\cdot\vec{a}}{\vec{a}\cdot\vec{a}}\vec{a} ,它和 \vec{a} 同方向,它是 \vec{a} 的 x 倍。事实上,投影还可以看作 \vec{p}=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}\vec{a}=(\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}})\vec{b} ,其中 \vec{b} 前面的部分 \frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}} 不再是数字,而是个矩阵,记为 P ,即 \vec{p}=P\vec{b} ,求一个矢量的投影,就是对这个矢量进行线性变换,也就是用矩阵乘矢量。投影矩阵 P 只和 \vec{a} 有关, P=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}} 。
我们看一个具体例子。将 \vec{b}=\begin{bmatrix}1\\1\\1\end{bmatrix} 投影到 \vec{a}=\begin{bmatrix}1\\2\\2\end{bmatrix} 所在直线,系数 x=\frac{\vec{a}^{T}\vec{b}}{\vec{a}^{T}\vec{a}}=\frac{5}{9} ,投影 \vec{p}=x\vec{a}=\frac{5}{9}\begin{bmatrix}1\\2\\2\end{bmatrix} 。我们可以验证一下 \vec{e}=\vec{b}-\vec{p}=\begin{bmatrix}\frac{4}{9}\\-\frac{1}{9}\\-\frac{1}{9}\end{bmatrix} ,\vec{e}\cdot \vec{a}=\begin{bmatrix}\frac{4}{9}\\-\frac{1}{9}\\-\frac{1}{9}\end{bmatrix}\cdot\begin{bmatrix}1\\2\\2\end{bmatrix}=\vec{0} , \vec{e} 与 \vec{a} 正交。
投影矩阵P=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=\frac{1}{9}\begin{bmatrix}1\\2\\2\end{bmatrix}\begin{bmatrix}1&2&2\end{bmatrix}=\frac{1}{9}\begin{bmatrix}1&2&2\\2&4&4\\2&4&4\end{bmatrix} ,它是个对称阵。 P 可以投影任何矢量到 \vec{a} 所在直线,例如本例中 \vec{p}=P\vec{b}=\frac{1}{9}\begin{bmatrix}1&2&2\\2&4&4\\2&4&4\end{bmatrix}\begin{bmatrix}1\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{5}{9}\\\frac{10}{9}\\\frac{10}{9}\end{bmatrix} 。
如果 \vec{b}=\vec{a} ,则有 x=1 ,矢量投影到自身仍是它本身。如果 \vec{b} 和 \vec{a} 正交,那么 \vec{b}\cdot\vec{a}=0 ,所以 x=0,\vec{p}=0 ,矢量在与它正交方向的投影为0。如果 \vec{a} 变为 2\vec{a} , P 是不变的,因为直线仍然是那条直线,所以投影和投影矩阵都不会改变,这是合乎预期的(但 x 会改变)。 P^{2}=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=\frac{\vec{a}(\vec{a}^{T}\vec{a})\vec{a}^{T}}{(\vec{a}^{T}\vec{a})^{2}}=\frac{\vec{a}\vec{a}^{T}}{\vec{a}^{T}\vec{a}}=P , 再投影一次是不会改变投影的,这也符合常识。
问题二:求 \vec{b} 在以 a_{1},a_{2}..a_{n} 为基的子空间 S 的投影。
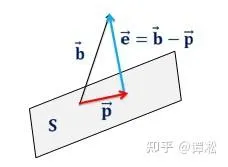
我们把 a_{1},a_{2}..a_{n} 作为矩阵 A 的列,这样一来以 a_{1},a_{2}..a_{n} 为基的子空间 S 就是矩阵的列空间 C(A) , \vec{b} 在 C(A) 的投影 \vec{p} 是 C(A) 中的矢量,自然可以表示成 Ax ,确定了 x 就知道了投影。 求解的关键依然是正交性:误差 \vec{e}=\vec{b}-\vec{p} 与 S 中所有矢量正交,等效于 \vec{e} 与 S 的基 a_{1},a_{2}..a_{n} 正交: \vec{a_{1}}^{T}\vec{e}=0,\vec{a_{2}}^{T}\vec{e}=0,...\vec{a_{n}}^{T}\vec{e}=0 , 用矩阵乘法表示为 A^{T}\vec{e}=A^{T}(b-Ax)=0 , \vec{e} 在 A 的左零空间中,我们通常改写为 A^{T}Ax=A^{T}b 。让我们停留片刻消化一下这个方程:本来 \vec{b} 不在 C(A) 中, Ax=b 无解;现在我们两边乘 A^{T} 改求 A^{T}Ax=A^{T}b ,这样解得的 x 作为系数对 A 的列线性组合得到的 Ax 是 C(A) 内最「接近」 \vec{b} 的矢量,也就是 \vec{b} 在 C(A) 的投影。
现在我们来求解。根据 A^{T}Ax=A^{T}b 解得 x=(A^{T}A)^{-1}A^{T}b , 进而得到投影\vec{p}=Ax=A(A^{T}A)^{-1}A^{T}b ,投影矩阵 P=A(A^{T}A)^{-1}A^{T} 。
细心的读者一定会在 (A^{T}A)^{-1} 这里停下来思考。 A^{T}A 是方阵,但它一定可逆吗?事实上我们在之前的文章中一再的证明过一个结论: A^{T}A 和 A 有相同的零空间。 当 A 的列线性独立, Ax=0 便只有 0 解,那么 (A^{T}A)x=0 也只有零解,即 A^{T}A 可逆。换句话说, 只要 A 的列线性独立,A^{T}A 就可逆。
投影矩阵 P=A(A^{T}A)^{-1}A^{T} 也颇具迷惑性。读者或许会想起矩阵相乘然后求逆的公式 (A^{T}A)^{-1}=A^{-1}(A^{T})^{-1} ,然后得出 P=A(A^{T}A)^{-1}A^{T}=AA^{-1}(A^{T})^{-1}A^{T}=I ,矢量在任意子空间的投影 P\vec{b}=I\vec{b}=\vec{b} ,这显











