袁讲经典13:一道碰撞问题的三种解法,看一看哪一种最妙!
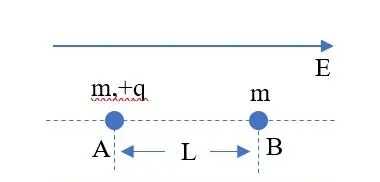
例: 如图所示,不记重力,空间有匀强电场 E 。有两个质量均为 m 的小球,A带电 q>0 ,B无电荷。 t=0 时,两球静止,且相距 L ,AB方向与 E 方向相同。 t=0 时刻,A开始受电场力而运动。A、B间发生弹性正碰,且无电量转移,求第8次正碰到第9次正碰之间需要的时间。
解1: 慢慢尝试计算,寻找规律,
首先,计算A在电场中运动的加速度,为, a=\frac{Eq}{m} ,
根据位移公式,计算A和B首次碰撞时间, L=\frac{1}{2}at_1^2 ,
解得, t_1=\sqrt\frac{2mL}{Eq} ,
此时, v_{A1}=at_1=\sqrt\frac{2EqL}{m} 。
然后发生第一次弹性碰撞,这里省略计算过程,直接根据「等质换速」得到碰撞后的速度为,
v_{A1}'=0 ,然后A做加速度为 a 的匀加速运动,
v_{B1}’=v_{A1}=\sqrt\frac{2EqL}{m} ,然后B作匀速直线运动,
再然后计算从第一次碰撞到第二次碰撞的时间,也就是再次相遇时间,得到,
\frac{1}{2}at_2^2=v_{B1}’t_2 ,
解得, t_2=2\sqrt{\frac{2mL}{Eq}} ,
再再然后计算,第二次碰撞前A和B的速度大小,
v_{A2}=at_2=2\sqrt\frac{2EqL}{m} , v_{B2}=v_{B1}’=\sqrt\frac{2EqL}{m}
碰撞后交换速度,得到,
v_{A2}’=v_{B2}=\sqrt\frac{2EqL}{m} ,然后作匀加速运动,
v_{B2}'=v_{A2}=2\sqrt\frac{2EqL}{m} ,然后作匀速直线运动,
计算相遇时间为, v_{A2}’t_3+\frac{1}{2}at_3^2=v_{B2}’t_3 ,
解得, t_3=2\sqrt{\frac{2mL}{Eq}} ,
此时,我们发现了, t_3=t_2=2\sqrt{\frac{2mL}{Eq}} ,
再次尝试下一轮碰撞,发现, t_4=t_3=t_2=2\sqrt{\frac{2mL}{Eq}} ,
所以,最终得到,第8次正碰到第9次正碰之间需要的时间也为 2\sqrt{\frac{2mL}{Eq}} 。
上述方法,原理上很简单,但是计算很烦躁,易乱,且不理解为啥两次碰撞的相邻时间间隔都是相同的,有一种弄通了一半的感觉。
解2: 变换参考系的方法,
由解法1可知,
第一次碰撞前, v_{A1}=\sqrt\frac{2EqL}{m} , v_{B1}=0 ,
第一次碰撞后, v_{A1}’=0 ,v_{B1}’=\sqrt\frac{2EqL}{m} ,
然后, 我们选择碰撞后的B为参考系 ,则,
B为静止的,
A以 \sqrt\frac{2EqL}{m} 速度反向减速到零,再正向加速到 \sqrt\frac{2EqL}{m} ,此时经历的时间为, t=2\sqrt\frac{2EqL}{m}/a=2\sqrt{\frac{2mL}{Eq}} 。
此时,A和B碰撞交换速度,在上述参考系中,交换速度后,
A的速度为 0 ,B的速度为 \sqrt\frac{2EqL}{m} ,
然后再次变换参考系, 选择新一轮碰撞后的B作为参考系, 则,
B是静止的,然后A相对B的运动同第一次碰撞后的情况,于是,
再次相遇碰撞的时间为, 2\sqrt{\frac{2mL}{Eq}} 。
所以,最终任意两次碰撞之间的时间间隔都为, 2\sqrt{\frac{2mL}{Eq}} 。
上述方法,计算量较小,也可以更好地从本质上理解为什么任意两次碰撞之间的时间间隔相等,但是呢?要从变换参考系的角度去理解呢,思维强度挺大的,费脑子。
另外,小伙伴们可能会提出来,动量守恒可以变换参考系使用吗?特别是「等质换速」在不是地面的参考系中能否使用呢?关于这个问题,我在文章「袁野:从一道经典习题浅议参考性等价及无穷小问题(2)」介绍过了,感兴趣的小伙伴,可以看一看哈!
解3: 我们可以采用图像法求解,应该是又简单快捷又形象易理解吧。如下,注意碰撞交换速度在图像中的体现,
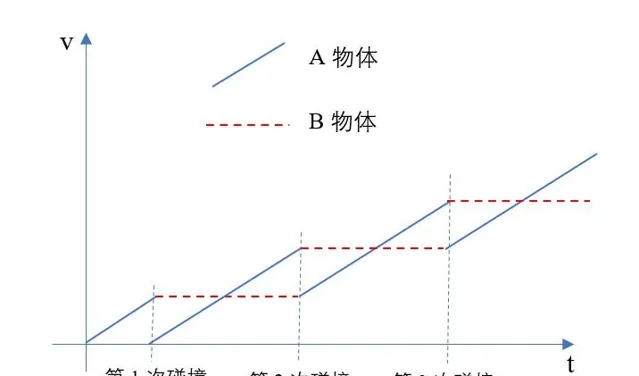
从图中可以看出,相邻两次碰撞的时间间隔都是相等的,且等于A物体从开始运动到第一次碰撞的时间的2倍,即 t=2t_1=2\sqrt\frac{2mL}{Eq} 。
好了,小伙伴们应该也发现了,哪种方法最简单了吧,图像法,直观,形象,好理解。
小伙伴们或许会问,什么时候用图像法呢?
其实关于运动学的问题,是我们进入高中学物理的第一阶段的知识点,个人认为还是挺难的,公式也多,方法有时候很巧妙。
我一般建议,在「单物体单状态」运动中,直接采用公式法,公式可以简单记为,
一个概念, 加速度 a 。
二个基本公式 ,
v=v_0\pm at , x=v_0t\pm\frac{1}{2}at^2 ,
三个连等式 ,
\bar{v}=\frac{x}{t}=\frac{v_0+v}{2}=v_{\frac{t}{2}} ,
四个导出结论 ,
v^2-v_0^2=2ax ,
\Delta x=aT^2 ,更一般为 x_n-x_m=(n-m)aT^2 ,
相等时间间隔位移比,
相等位移间距时间比。
具体在文章「袁野:斜面问题如何做的对,做的快,做的漂亮」中,最后有一些关于这方面的介绍。
而这里建议采用公式计算的,主要是「单物体单状态」,所谓的「单状态」,小伙伴们要深入理解一点点,这个「单状态」包含了加速度不变的往返运动,比如竖直上抛运动,很多小伙伴喜欢把竖直上抛运动当做「多状态」运动,先计算上抛过程,再计算自由落体过程,其实大可不必,我们可以把它看做一个「单状态」,因为,我们上面的公式都是「匀变速」运动公式,换句话说,只要加速度不变,就是一个状态,不需要分解过程的。
而当加速度变化时,就是「多状态」了,另外还有可能存在「多物体」,对于「多物体多状态」的情形,我们需要分物体考虑,还需要分状态考虑,因此计算过程相对较为复杂,此时可以考虑采用其他方法,比如变换参考系,让一个物体不动,再比如,用 v-t 图像法,显然,上面这道题属于「多物体多状态」,于是考虑了图像法。
这里,我再跟小伙伴们分享一些关于图像法的运用,比如,在文章「袁野:变换参考系在高中物理运动学解题中的妙用」中,有一道例题,原文章采用了变换参考系的方法,题目如下,
例: 在空中某处以初速度 v_0 竖直向上抛出一个小球A,与此同时,在小球A正上方H处有一小球B自由释放下落,问小球A和小球B在空中相遇的时间?已知重力加速度为g,不计空气阻力,相遇时两小球均未落地!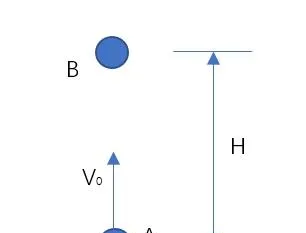 仔细想想,这题是多么复杂呀!我们要讨论以下三种情形:
仔细想想,这题是多么复杂呀!我们要讨论以下三种情形:
1.在小球A上升过程中相遇;
2.在小球A上升后又下降过程中相遇,但未下降到抛出点,仍在抛出点之上;
3.在小球A下降过程中相遇,且在抛出点之下。
这里,我再使用图像法计算,发现根本不需要考虑上面所说的三种情形,如下,
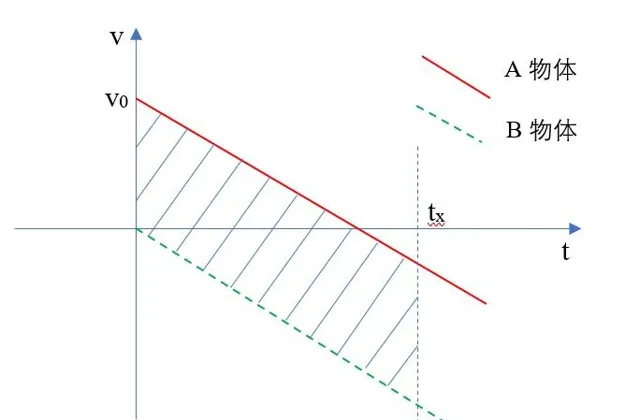
如上图所示,无论在什么情况下相遇,我们从图中只要明白一件事,就是两条速度直线所包围面积为 H 时,即为两小球相遇,且图中两条直线的斜率均为 g ,因此,所包围面积为平行四边形,且面积为 H 时,计算时间为, v_0t_x=H ,所以, t_x=\frac{H}{v_0} 。
多简单,是吧!
上次还有小伙伴问这样一道题目,大致意思是说,
例: 如下,水平传送带以一定速度顺时针转动,每隔时间 T 在传送带上静止释放一个物块,物块与传送带之间的动摩擦系数为 μ ,最终物块在传送带上运动稳定后,物块与物块之间的距离为 x ,求传送带的速度大小?
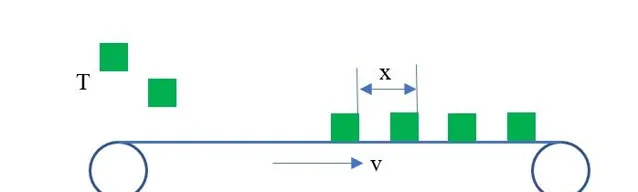
这里,我也不多解释了,直接画出 v-t 图像如下,
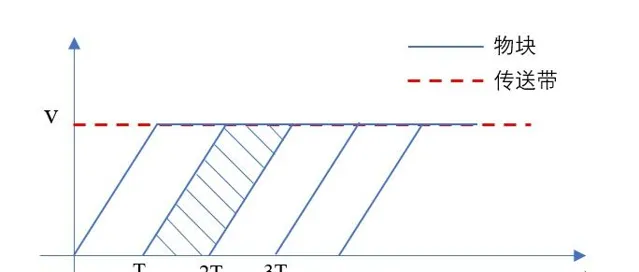
直接解得,传送带的速度大小为, v=\frac{x}{T} 。
好了,关于这道经典例题,就分享这么多吧!
小伙伴们,咱们期待下次相遇经典!











