看了很多回答,好像理解起来感觉还是 ......有点勉强,依然让人觉得很「玄学」!我试试用一种初中物理水平就可以理解的方式聊聊这个问题。
本来零极点就是各种线性物理对象数学的抽象,不是简单的特指某个元件,倒不如这样说更准确,一个信号经过一个零点或极点的作用后,会有什么影响或变化!因为增加一个极点或一对极点(零点一样),本质上就是传递函数上多乘了一个环节,也就是上一个环节出来的信号,再经过这个环节大概会发生如何的变化。
先说一下极点,极点就两种情况,一种是实轴上的极点,一种是共轭极点,再复杂的线性系统都是由他们所组成的。先看单个实轴上的极点,呃,增加了一个极点,这……不就是信号又经过了一个惯性环节吗?我们知道,一个阶跃信号经过一个惯性环节,经过3到4个 \tau (时间常数)差不多就进入稳态的信号。我们先做个小实验,如下图。
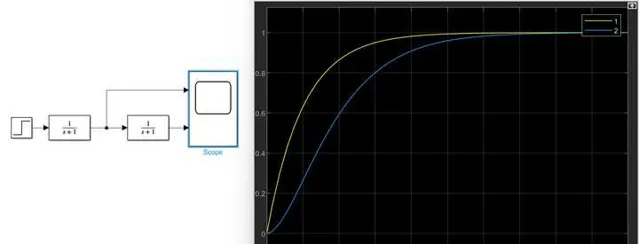
这个图很简单,关键怎么去理解他。看黄色的曲线1,学自控的都懂,太熟悉了,一个阶跃信号经过一个惯性环节后本来陡峭突变的曲线变成了前面变化快,然后变化变慢的上升曲线,并且3到4个 \tau 的时间后就达到稳态。也就是说,一个激励,或一个信号,经过一个极点的环节之后,由于受到一阶惯性的作用,他变缓了!用自控的语言说,上升率变慢了,上升时间和调节时间增加了。所以再看蓝色曲线2,就是曲线1又经过了一个极点后的情况,所以他肯定更缓了!而且不可能会多出一个震荡出来,毕竟阶跃那么剧烈的信号经过惯性环节都没引发震荡。所以说每多一个负实数极点就是让响应变缓,不管他在哪个负实数位置,位置只是影响变缓的程度。
那不同位置的极点(就是时间常数不同),影响的程度有多大呢?看下面的图,时间常数分别是0.1,1,10的惯性环节(对应极点位置-10,-1,-0.1),阶跃信号经过这些环节的处理之后信号变化的情况。

既然阶跃信号经过极点是这样的效果,那其他信号大家可以想象出来吗?如果极点的位置离虚轴越近(就是时间常数越大,用ts+1=0,求极点位置),减缓的作用越强,反之减缓作用越弱。比如我们试试看用一个二阶震荡环节,分别经过时间常数不一样的惯性环节,一个时间常数远小于二阶的时间常数,一个在同一个数量级,一个高于一个数量级的,看看效果如何?为了大家看得舒服,我直接把结果放出来,自己琢磨一下。
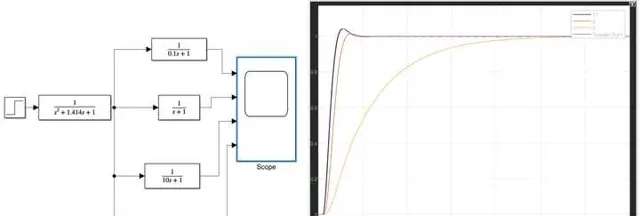
紫色的是典型的二阶欠阻尼信号,时间常数是1,可以看出来,经过时间常数是0.1的极点,响应曲线基本不变,经过同一级别时间常数的,响应变缓了,超调减少了,经过时间常数是他10倍的,那影响大了,连震荡都缓没了!所以我们的教材在二阶系统的零极点影响那里都会介绍,具有负实数极点动态特性的震荡线减弱,上升时间和调节时间增长,超调减少,也就是惯性增强了。多了一个极点,就是多乘以一个惯性环节,惯性不增强了才怪!这,不就是简单的线性思维的推论吗?
如果这种说法对大家有帮助,有一点点赞或收藏,我再继续说其他的影响。不过按照这种物理思维实验的方式,应该对大家有了足够启发了。








