[文末提供原文PDF免费下载(期刊论文版式)]
摘要 :运动规划是自动驾驶系统中承上启下的一环,本文综合分析运动约束类型,并将运动约束转化为惩罚函数,求解最佳速度的解析解,采用数值仿真手段,生成与最佳路径耦合的最佳速度曲线,并分析速度曲线的跟随特性。
01
引言
在前文【 设计搭建汽车机器人 】中详细阐述了MCR的硬件系统,其中感知系统依赖的传感器是ZED双目相机和激光雷达,获取机器人周围环境信息。
从自动驾驶系统层面分析,环境感知子系统的作用是将机载传感器获取的自然环境信息生成地图模型,具体可参考【 机器人环境感知研究现状简述 】。

图 1.1 汽车机器人MCR模型
参考【 机器人环境感知研究现状简述 】提出的算法,深入分析道路场景的特点及应用需求,基于MCR平台设计了感知系统,并在【 基于激光-视觉的环境感知建模方案与应用 】一文中展开了详细阐述,最后基于该建模方案,生成了简洁、高效的几何特征地图。
【 基于激光-视觉的环境感知建模方案与应用 】得到的规划地图模型包含了道路、障碍物及机器人的信息,是机器人运动规划的依据。本系列运动规划文章将采用路径-速度解耦规划框架,综合分析环境约束、机器人运动约束,从安全适用、实时可靠的角度出发,设计综合性能强的完整运动规划模型,如图 1.2所示,共包含初始路径规划及路径优化、速度优化和运动控制求解四个子模型,将基于规划地图模型直接驱动机器人沿规划结果轨迹运动。
前文详细阐述了【 路径优化模型设计 】,本文将在路径优化模型之上主要介绍速度规划模型设计及建模方法,后续系列文章会综合阐述运动规划模型。
(点击或阅读PDF原文查看大图)
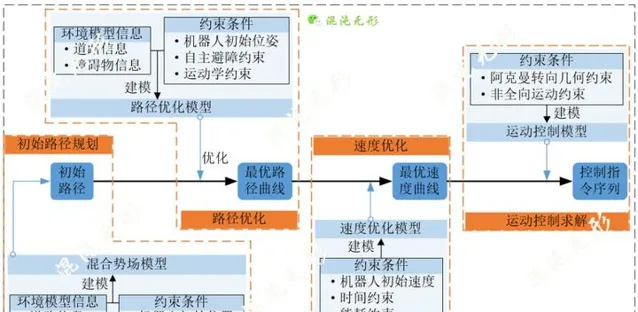
图 1.2 运动规划模型流程
轨迹曲线是路径曲线和相耦合的速度曲线组成的,仅有最佳路径曲线并不能完整描述机器人运动状态。故,综合考虑能耗、目标跟随等约束,设计速度曲线优化模型,基于最佳路径曲线,生成最佳速度曲线。
02
速度优化变量
如图 2.1(a)所示,机器人从状态 S rk 变化到 S rk +1,需要满足非全向约束(仅能做直线或圆弧运动),结合路径曲线序列(参考【 路径优化算法设计 】)的曲率,可表示为
式中,[
vsk
,
wsk
]与 [
v
sk
+1,
w
sk
+1]分别表示状态
S
rk
和
S
rk
+1的线速度、角速度,转弯曲率
ρ
=1/
r
。
已知初始速度[ v s 1, w s 1],由式(1)知,线速度和角速度求其一即可,因此速度优化问题转化为求解 S rk 变化到 S rk +1的线速度变化量Δ v k,k +1,即Δ v k,k +1是优化变量。
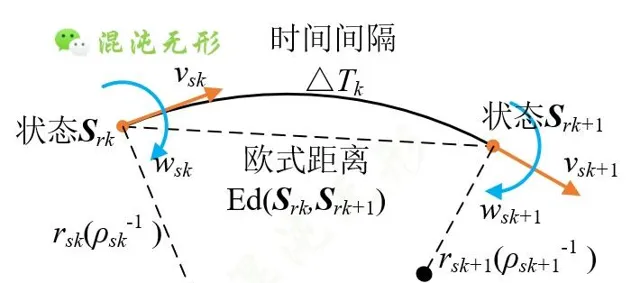
(a)状态变换图
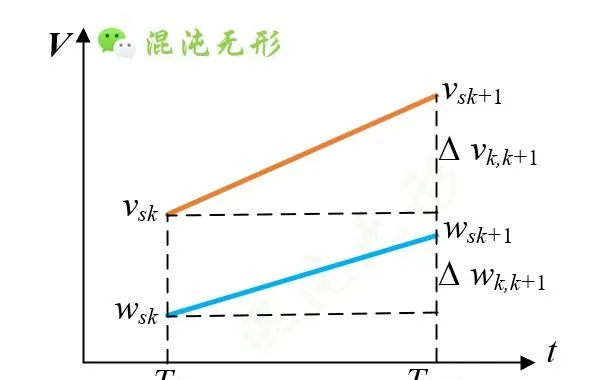
(b)速度变化图
图 2.1 运动约束示意图
03
约束条件
参考图 3.1,除路径约束外, State 还需要满足速度约束。机器人运动需在极限速度范围[ vmin , vmax ]和加速度范围[ amin, amax ]内,表示为
式中, vk ( S rk )与 ak ( S rk )分别表示机器人在 S rk 状态时的运动速度和加速度。
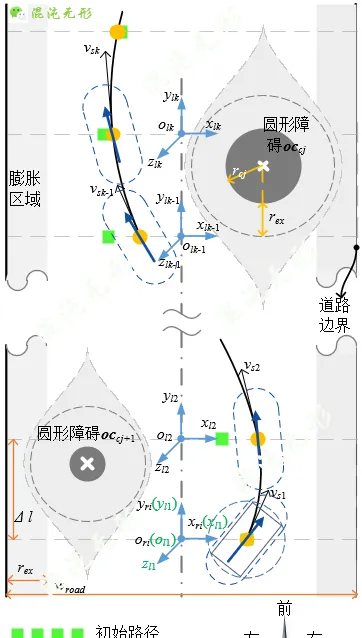
图 3.1 轨迹规划及优化模型示意图
除式(2)中的极限约束之外,还需要满足机器人运动能耗、时耗及目标速度跟随等要求,具体如下:
3.1
能耗约束
机器人运动可视为平面刚体运动,由动能定理 Ek =( mv )^2/2+( Iw )^2/2,可知速度波动(变化量)越大,则能耗越大,且会降低机器人运动平稳性。因此,机器人能耗可表示为
式中, km 表示速度变化量系数, kI 表示角速度变化量系数,Δ w k,k +1表示状态 S rk 到 S rk +1的角速度变化量。
结合式(1),得到角速度变化量与速度变化量之间的关系
3.2
时间约束
如图 2.1,时间间隔Δ Tk 与速度、路程有关,由于相邻状态间距小、机器人转弯半径大,因此,「以直代曲」估算相邻状态的距离,并假设机器人在Δ Tk 内为匀变速运动,因此时间间隔约为
式中, Ed ( S rk , S rk +1)表示相邻状态之间的欧式距离。
3.3
目标速度跟随约束
机器人运动速度是可根据操控者或决策模块调控的,因此,速度曲线需要跟随目标速度 v tg 的变化,采用速度差值Δ v tg 来衡量跟随的效果,表示为
04
优化目标
4.1
目标函数
速度优化属于多目标优化问题,与路径优化的处理方式相似,将速度约束转化为无约束的综合惩罚函数,表示为
式中, Jk 表示 S rk 到 S rk +1的速度成本函数,[ λw λv λT λtg ]分别表示各项惩罚项的权重系数;(Δ w k,k +1)^2+(Δ v k,k +1)^2为能耗惩罚项,惩罚速度变化量过大的情况;Δ T k -1为时间惩罚项,惩罚为跟随速度过快而导致的运动时间变短的情况;(Δ vtg )^2为目标速度跟随惩罚项,让机器人运动速度保持在目标速度附近。
最终,优化目标转化为求解综合成本最低的无约束优化模型
式中,Δ v k,k +1*表示相邻状态下最佳速度变化量。
4.2
优化求解
将公式(3-7)带入(8)中并化简, J k 是关于Δ v k,k +1的二次函数,对 J k 求导,得到最小值
根据式(9), v sk +1 =Δ v k,k +1* + vsk ,同时 vsk +1需要满足约束(2)。本文仅考虑机器人前向运动,因此速度区间为
式中,set( vsk +1)表示状态 S rk +1的速度可行域, ν ( a )表示加速度限制下的速度大小,表示为
判断 vsk +1是否在可行速度区间set( vsk +1)中,求解实际最优速度 vsk +1*,具体如下
综合式(2-12),得到 S rk +1处的实际最优速度 vsk +1*,以及Δ T k 。已知路径曲线序列(参考【 路径优化算法设计 】)和 v s 1,可生成最佳速度曲线序列 V:
式中, V sk = [ vsk , wsk ]。最终,结合路径曲线序列(参考【 路径优化算法设计 】)和最佳速度曲线序列得到 State ,包含时序的机器人运动状态序列可表示为
05
优化结果分析
图 5.1(b)中速度曲线及基于图 5.1(a)中的最优路径曲线生成的,通过调节目标速度,可调节机器人速度,当目标速度变化的时候,速度曲线立即响应,速度的平稳性决定于加速度设置范围。而速度曲线没有完全达到目标速度的原因是速度优化包含多种目标,速度跟踪权重设置到无穷大,则可完全达到目标速度。
(横屏或阅读PDF原文查看大图)
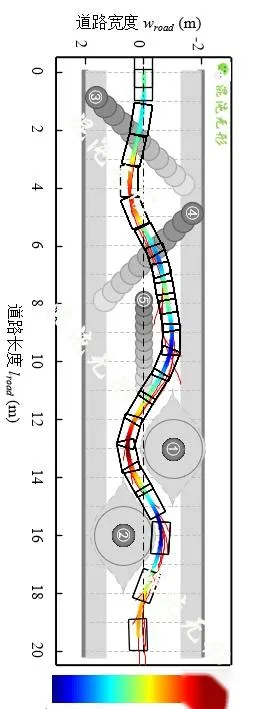
(a)运动规划状态图
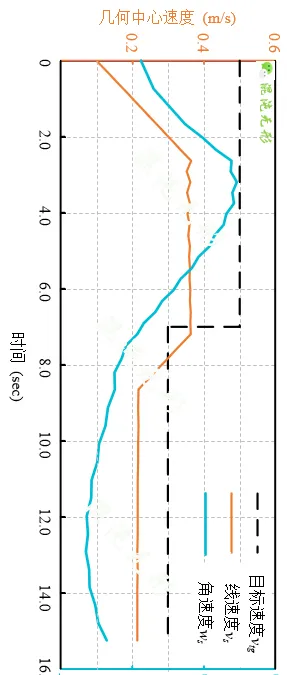
(a)速度优化曲线
图 5.1 直线道路场景运动规划结果
06
结论与展望
本文综合分析机器人运动约束,并将运动约束转化为惩罚函数,求得了最佳速度的解析解,生成了与最佳路径耦合的最佳速度曲线,分析了速度曲线的跟随特性,后续会将该速度曲线转化为机器人运动控制参数,驱动机器人运动,敬请期待。
(文章仅笔者个人分析,有误请指正,谢谢!)
福利放送
笔者为小伙伴们整理了 期刊论文版式原文PDF ,方便收藏和回味
需 将此文分享到到朋友圈,并集齐10个赞,截图发送后台或发送邮件:[email protected],审核通过后,回复下载链接。
注意 :原文PDF效果可参考之前(2022年8月21日)的文章末尾的下载链接,如
Car-like Robot运动模型及应用分析
延伸阅读
设计搭建汽车机器人(M1)
基于激光雷达的场景建模算法分析与应用(M2)
基于视觉的场景建模算法分析与应用(M3)
基于激光-视觉的环境感知建模方案与应用(M4)
汽车机器人路径规划算法之混合势场模型设计(M5)
汽车机器人路径规划算法之初始路径规划算法设计(M6)
汽车机器人路径规划算法之路径优化算法设计(M7)
机器人运动规划算法研究现状简述
机器人空间采样算法研究现状简述
机器人图规划算法研究现状简述
机器人环境感知研究现状简述
常见移动机器人运动学模型总结
Car-like robot运动参数校准
-----------------------------------------------------------------------------
相关声明
1.如果转载本文,文末务必注明:「转自微信公众号:混沌无形」
2.若有侵权,请联系作者


全文完,感谢阅读!!如果觉得写的不错,那就点个赞或者「在看」吧。











