要快速處理連續碰撞問題,首先要把一些基本的一級結論和二級結論背熟。
一、處理彈性碰撞中的基本方法
一般的復習書中都會給出彈性碰撞的兩個守恒式:
m_{1}v_{1}+m_{2}v_{2}=m_{1}v_{1}^{'}+m_{2}v_{2}^{'}; \frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}m_{1}v_{1}^{'2}+\frac{1}{2}m_{2}v_{2}^{'2}
解出:
v_{1}^{'}-v_{2}^{'}=v_{1}-v_{2}
也就是在彈性碰撞中利用動量守恒和機械能守恒可以得到一個等價的式子,那就是
靠近速度=遠離速度(符合條件可以作為二級結論使用)
這個式子其實就是恢復系數e=1的等價。
在實際的彈性碰撞中我們往往會扔掉機械能守恒定律的式子,因為它的運算式中關於速度的都是平方,不易求解。
實戰中往往寫出動量守恒式子和恢復系數為1的式子來聯立求解,因為這兩個式子中出現的速度都是一次方,求解起來非常方便。
二、彈性碰撞中的一個基本模型——動物撞靜物
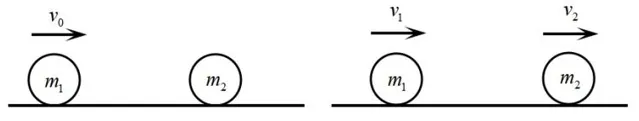

討論幾個特殊情況:

好了,記住以上這些基本結論,讓我們開始解題。
三、問題處理
題1.(2020年中國科學技術大學創新班考試物理試題第2題)三個相同的、品質均為m的小滾軸(分別編號為1,2,3)排成一行,靜止在光滑水平面上,每個滾軸之間有間距。現有一品質為M(M>m)的大滾軸以速度從左方沿3個小滾軸連線的方向射向小滾軸,若大滾軸與小滾軸,小滾軸與小滾軸之間的碰撞都是完全彈性的,試求所有滾軸的最終速度。


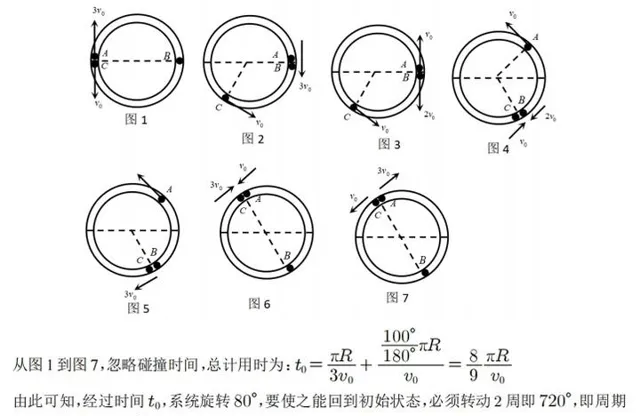
②考慮一個非常有趣的事情,右側只有1個小滾軸,但是小滾軸的右側還有一堵墻,那麽小滾軸每次碰墻之後從墻那裏獲得了反向的沖量,再回頭撞擊M,總有一天會讓M向左運動,於是可以命制下題:

解析:這是在2020年左右轟動全世界物理學界的一個碰撞實驗。
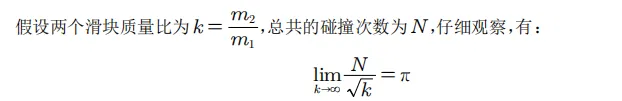
關於上式的證明,可以參考以下文獻:
1.程軍,孫輝.關於物塊碰撞次數的探討[J].大學物理.2020,39(08):11-13.
2.嶽國聯等.用矩陣研究一維彈性碰撞與圓周率的關系[J].大學物理.2022,41(08):19-25.
3.陳怡.碰撞出來的圓周率——兩球與墻壁三者間的碰撞次數與圓周率π間關系的討論[J].物理與工程.2020,30(01):68-72.
4.文世達等.兩球彈性碰撞次數與它們品質之比的關系研究[J].物理通報.2018,(12):120-122.
5.彭定輝.用矩陣方法處理物塊碰撞次數問題[J].物理通報.2021,(02):63-64,67.
6.王富強等.一維完全彈性碰撞次數和圓周率[J].物理與工程.2022,32(02):65-73.
7.李開瑋.滾軸碰撞動力學與圓周率的關聯[J].力學與實踐.2021,43(01):108-111.
8.許劍偉,吳瓊煙.碰撞次數與圓周率[J].湖南中學物理.2022,37(03):73-76.
9.葉誌煒黃樹清.彈性碰撞與圓周率的奇妙聯系[J].物理教學探討.2022,40(07):59-61.
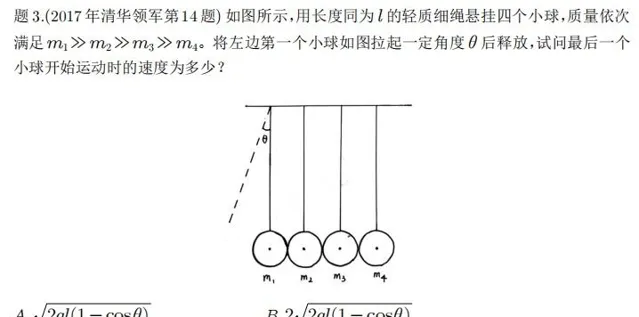
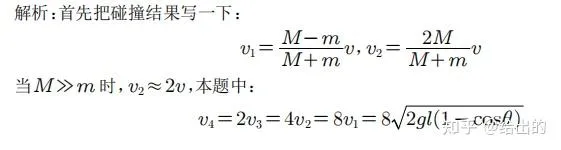









四、結語
連續碰撞問題的處理其實是很套路的,只要記住基本模型的一級結論即可。(需要二級結論和其他高考物理資料可si)











