高中物理極值問題,是考試中經常出現的一類,極值的出現往往伴有相同的條件,運動學中出現極值往往速度相等,力學中出現極值往往合力為零,電學中出現極值往往是功率最大或者最小,帶電粒子在磁場中出現極值往往速度相切、圓心角最大或最小等等,但還有一類的極值比較隱含,就是「三分之二」引起的極值問題,這類問題往往對學生的理解歸納能力、數學計算能力有較高的要求。
本文分別從高中物理幾個不同的知識點例題入手,舉例說明「神奇三分之二」的存在。
例題1 豎直平面內有一個四分之一圓弧AB,OA為水平半徑,現從圓心O處以不同的初速度水平丟擲許多個相同品質的小球,小球可以看作質點,不計空氣阻力,小球落到圓弧上時最小的速度為多少?
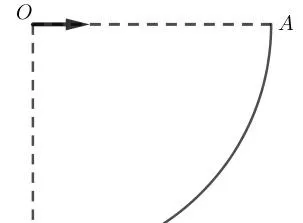
解析:定性的分析,小球平拋的初速度越小,小球落點離B點越近,重力做功越大;小球平拋的初速度越大,小球落點離B點越遠,重力做功越小。很明顯透過定性的分析判斷不了落在哪個位置動能小,但可以隱約察覺到在A和B之間弧上的某一點上,需要做定量計算。
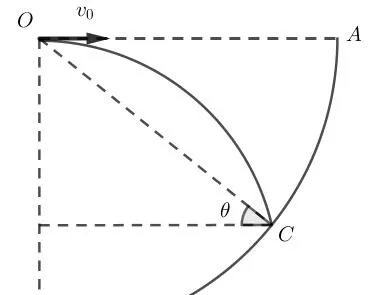
如上圖所示,設四分之一圓的半徑為R,小球丟擲的初速度為Vo,小球落在圓上的速度為V
豎直方向:

水平方向:
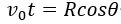
聯立上面兩式可得:
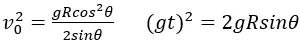
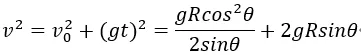
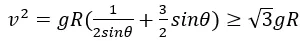
若且唯若
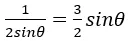
,等號成立,可得

當gR=10時,透過GeoGebra模擬速度與的變化如下圖所示
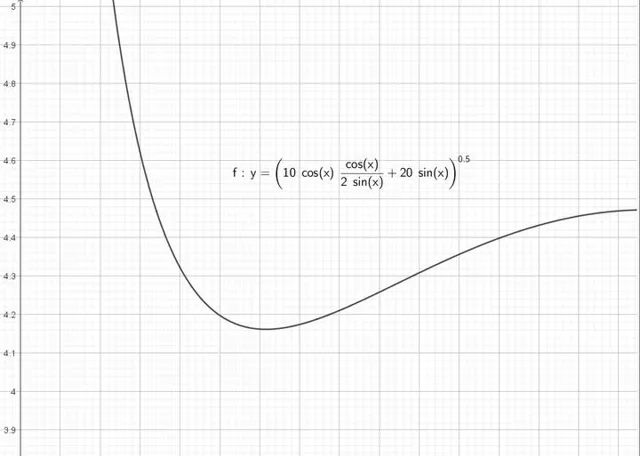
例題2 光滑的半圓弧面固定在水平面上,一可以看成質點的物塊從半圓弧面頂端靜止滑下,問物塊下滑的過程中,物塊何時脫離半圓弧面?
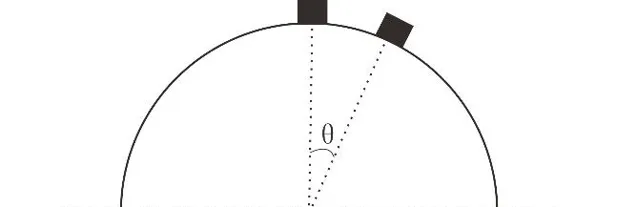
解析:滾軸脫離弧面時,滾軸與弧面間的作用力為零,此時滾軸做圓周運動的向心力恰好由其重力沿著弧面半徑方向的分量提供,大小為mgcosθ
整個過程中對滾軸由動能定理:
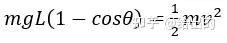
由
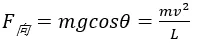
,可得
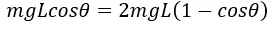
解得 cosθ=2/3
例題3 如下圖所示,光滑的墻角豎直放置著一根長為L的輕桿,輕桿兩端固定著兩個品質為m的A、B小球,現B球受到輕微擾動向右運動,問A球何時脫離墻面?
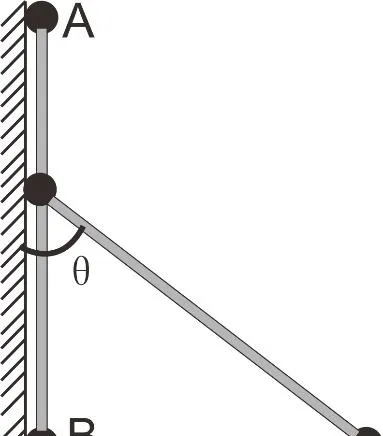
解析:當A球恰好要離開墻面時,輕桿的作用力為零,此時A球做圓周運動的向心力恰好由其重力沿著桿方向的分量提供,大小為mgcosθ
整個過程中對A由動能定理
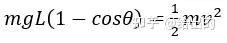
由
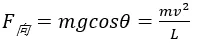
,可得
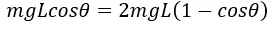
解得 cosθ=2/3
例題4 如下圖所示,長度為L輕細線一端固定於O點,一端系一品質為m的小球,水平拉直細線,在豎直面內將小球靜止自由釋放,問何時重力功率最大?
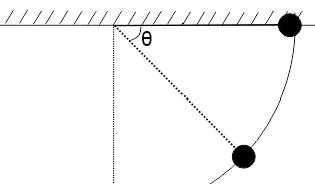
解析:如上圖所示,當細線與水平方向成θ時
對小球:
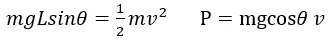
聯立得:

令
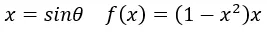
,對X求導可得
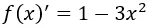
當
時,f(x)有最大值,即

時,功率P有最大值。
例題5 在同種點電荷形成的電場中,點電荷中垂線上的電場強度何時最大?
解析:設兩點電荷之間的距離為2L,中垂線點與點電荷的連線和水平方向成θ。
令
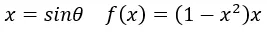
,對X求導可得
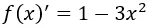
當
時,f(x)有最大值,即

時,電場強度最大。
例題6 如下圖所示,豎直的半圓弧局域中存在垂直紙面的磁場,一根金屬桿從半圓弧上端水平自由下落,問何時金屬桿產生的電動勢最大?
解析:桿做自由落體運動,下降h時的速度
此時切割的長度 L=2Rcosθ
金屬桿產生的電動勢
令
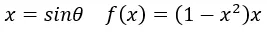
,對X求導可得
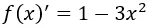
當
時,f(x)有最大值,即

時,金屬桿產生的電動勢最大。











