
我們已經開始接近黎曼猜想,回顧一下前兩篇的內容:
用最簡單的方式解釋黎曼猜想(一),理解質數定理
用最簡單的方式解釋黎曼猜想(二),黎曼ζ函式,質數之門的金鑰匙
我們已經知道,如果s是某個大於1的數,那麽zeta函式如下:
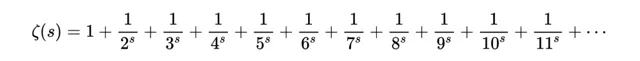
或者用求和符號表示:
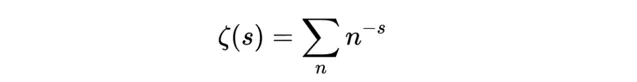
我已經展示了,透過套用一個過程(非常像埃拉托色尼的篩選法),它是如何等價於:
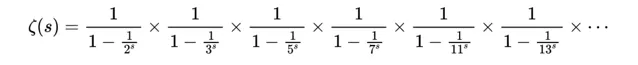
整理得:
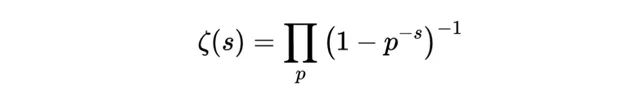
因此有:
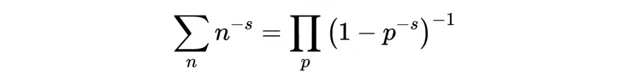
歐拉乘積公式
到目前為止,一切都很順利。但什麽是非平凡零點?函式的零點是什麽?zeta函式的零點是什麽?它們什麽時候是「非平凡」的?我們繼續!
先忘記黎曼zeta函式,考慮下面的函式:
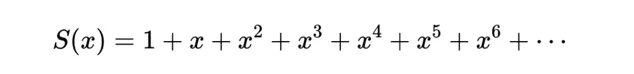
這個函式收斂嗎?為了對這個函式有個直觀的感受,我們先看一個例子。
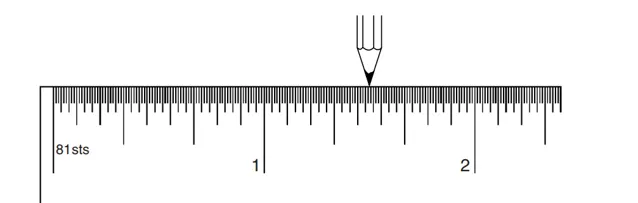
拿一個標有四分之一、八分之一、十六分之一……的普通尺子。用鉛筆尖指著尺子上的第一個標記,零。把鉛筆向右移1(單位)。鉛筆尖在「1」的標記上,總共移動了1個單位,如下圖1:

圖1
現在,把筆尖向右移動0.5個單位,如圖2:
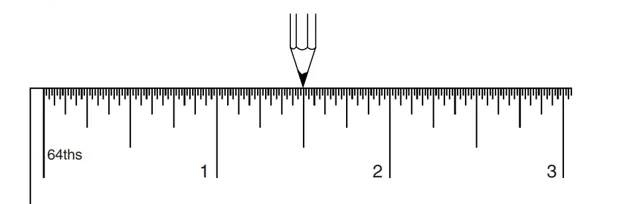
圖2
繼續把筆尖向右移動1/4,1/8,1/16,1/32,1/64。現在,你的筆尖在圖3的位置:
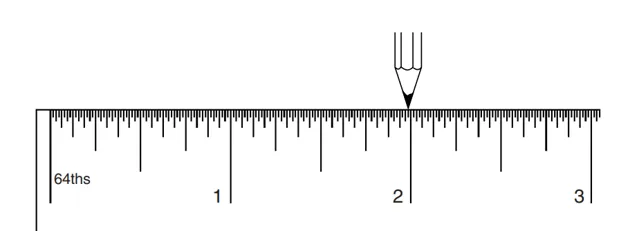
圖3
筆尖移動的距離是:
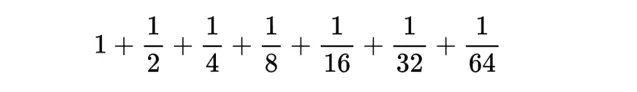
容易算出的結果是:
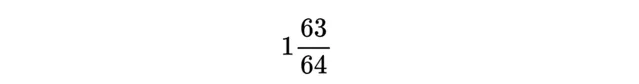
顯然,如果能像這樣繼續下去,每次減半距離,會越來越接近2,但永遠也到不了2(可以無限接近)。我們可以把這個事實表示成:
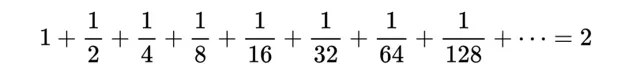
假設筆尖先向右移動一個單位,再向左移動0.5個單位,再向右移動1/4個單位,再向左移動1/8個單位……,如圖4:
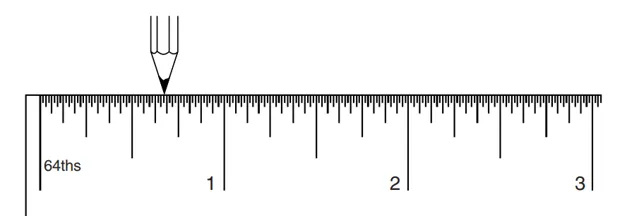
圖4
因為從數學的角度來看向左移動等於向右負移動,這就等於:
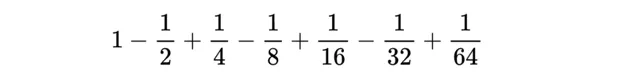
結果是43/64。如果繼續加、減無窮項,就會得到:
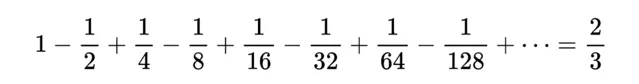
如果是1/3呢?
如果你自己動手去移動,不難發現,移動總距離不超過3/2,也就是:
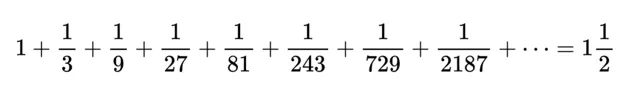
同理可以知道:
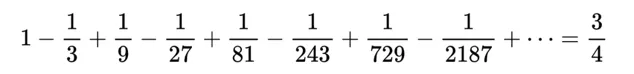
回到函式S(x),計算S(x)函式值如下:
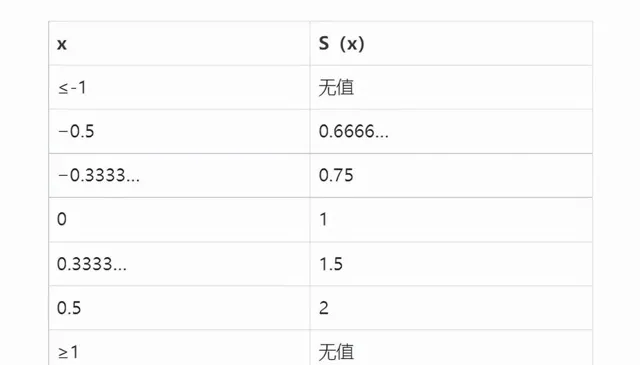
畫出函式圖如下:
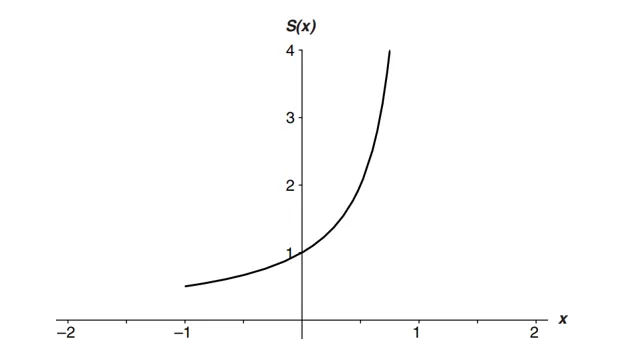
在-1的左邊和1的右邊,函式沒有值,也就是這個函式的定義域是[-1,1]。
但我可以換個方式表達函式,如下:

看出什麽了嗎?右邊括弧裏的內容不就是S(x)嗎?也就是說:
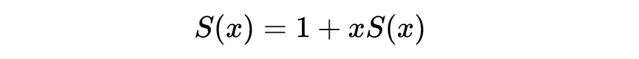
把最右邊的一項移到等號左邊:

也就是:

因此:
也就是:
對嗎?某種程度上是。因為它們的定義域不同。1/(1-x)函式圖如下:
上面的例子說明的是,無窮級數可能只定義了函式的一部份,函式的其余部份可能隱藏在某個地方,等待著被某些技巧發現(解析延拓),就像我用S(x)做的那樣。
這就引出了一個問題: 黎曼zeta函式也是這樣的嗎? 有沒有可能zeta函式:
比(1,∞)更大?
是的,zeta函式的自變量可以小於1。事實上,像1 / (1 - x)一樣,除了x = 1之外,它在每個數位上都有一個值。
了解一個函式需要時間、耐心和仔細的研究。我可以畫出zeta函式的函式圖:
當s<1時,zeta函式的函式圖。
當s小於1時,我如何得到ζ (s)的這些值的呢?前面我們已經討論過,,s是要大於1,zeta函式才有值。如果我要計算ζ(-7.5),我該如何開始?
這個我不能完全解釋,因為它需要太多的微積分。不過,我可以給出大致的思路。首先,讓我定義一個新函式,即eta(η)函式:
不是不斷地增加數位,而是交替地增加,然後減少,所以每一個數都會在一定程度上抵消前一個數的影響。數學家可以證明,這個新的無窮級數在s大於0時收斂。這是對zeta函式的一個很大改進,zeta函式只在s大於1時收斂。
這對我們了解zeta函式有什麽用呢?首先註意代數的基本事實:A − B + C − D + E − F + G − H + …等於(A + B + C + D + E + F + G + H + …)減去2 × (B + D + F + H + …)。
所以我可以重寫η(s):
減去
第一個括弧當然就是ζ (s),我可以提出1/(2^s),得到:
或者,反過來寫,最後整理一下:
這意味著,如果我們計算出η(s),那麽我就能得到ζ (s)的值。由於我能算出η(s)的值在0和1之間,我也能得出ζ (s)的值也在那個區間上, 盡管事實上原始的ζ (s)在這個區間不 收斂。
假設s為1/2。η(s)的前100項之和為0.555023639…;前1000項之和為0.599898768….。事實上η (1/2)的值為0.604898643421630370。有了這些,我可以計算ζ(1/2)的值了,得到−1.460354508…,這看起來很正確。
但是,當s為1/2時,我如何處理這兩個無窮級數,畢竟它們有一個收斂,有一個發散。嚴格地說,我不能,而且我在這裏的數學運算上有點跑偏了。但是我得到了正確的結果,在區間(0,1)上,可以用這個方法計算出任何ζ (s)的值。
現在,除了在s=1處,我們已經可以把ζ (s)的定義域擴大到大於0的區間上。 但是小於等於0的情況呢? 問題開始變得復雜了。黎曼1859年論文中的一個結果證明了一個由歐拉在1749年首次提出的公式,用ζ (1 − s)代替ζ (s)。例如,如果你想知道ζ (−15)的結果,你可以計算ζ (16),然後帶回到公式中,這是一個很復雜的公式:
黎曼能想到這一點,確實驚為天人,很多專業數學家都非常驚訝!
這個公式中涉及到了階乘,學過高等數學的或許知道,有一種方法可以定義除負整數之外的所有數的階乘函式,我不在這裏討論。下圖是-4到4的階乘函式圖:
如果你覺得有點上頭,只要相信有一種方法可以得到任何數位s的ζ (s)的值,除了s = 1這個唯一的例外。
我想說的是「 1 / 2」 在ζ(1−s)和ζ (s)之間的關系中具有特殊的地位!
因為如果x=1/2,那麽1-s=s。很明顯,從上面的影像看,zeta函式不是關於s=1/2對稱的;但1/2左邊的函式值與1/2右邊的映像值以一種緊密而復雜的方式聯系在一起。
回頭觀察一下s<1時的函式圖,會發現zeta函式在負偶數處的值都為0。
如果一個函式在某些值處的函式值為0,這些值就是該函式的零點。
因此,−2,−4,−6,…和所有其他負偶數都是zeta函式的零點。
這裏回顧一下黎曼猜想的陳述:
黎曼zeta函式的所有「非平凡零點」的實部都是1/2。
這裏麵包含了「非平凡零點」,我們已經越來越接近了!負偶數確實是zeta函式的零點,但是它們不是「非平凡零點」,而是「平凡零點」。 對於非平凡的零,我們還需要深入研究











