前言:
網上關於使用pytorch復現SRCNN的文章和程式碼已經多如牛毛,為什麽我還要寫這篇文章呢?
這是因為在我一開始學習超分辨率網路時,發現網上的程式碼並沒有嚴格按照論文中的表述進行復現,對數據的處理和評價指標PSNR的計算也沒有與論文達到一致。
這些問題導致網路的輸出結果與論文無法在相同標準下比較,帶來了很大的麻煩。例如,因為python和matlab的插值演算法等與論文不同,導致PSNR的數值與論文的數值不在一個baseline。這些問題導致復現的結果無法直接與論文結果比較,從而無法確認我們是否真的正確復現了論文,這對學習超分辨率網路是有害的。如果一開始的路就歪了,那之後想要糾正就會付出更大代價。
以上種種,促成了這篇文章(可能之後會有一個系列)的誕生。本文 不會詳細介紹網路的原理 ,文章的目的主要是記錄SRCNN的復現過程,同時將復現時一些容易出現錯誤的細節問題進行總結,做到 盡量正確還原論文結果 。如有錯誤,歡迎指正!
論文:SRCNN官方網站(含論文和caffe程式碼)
我的程式碼:Pytorch復現SRCNN
轉載請附加原文連結。
一、網路的結構
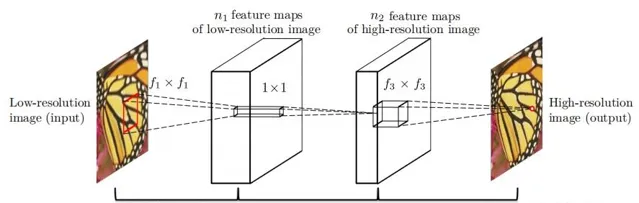
SRCNN的網路結構很簡單,只有3層摺積網路。前兩層使用ReLU啟用函式。
一些表示的說明:
因此論文中的SRCNN網路可表示為: Conv(1,64,9)-ReLU-Conv(64,32,1)-ReLU-Conv(32,1,5)
Pytorch中的實作方法:
class
SRCNN
(
nn
.
Module
):
def
__init__
(
self
,
padding
=
False
,
num_channels
=
1
):
super
(
SRCNN
,
self
)
.
__init__
()
self
.
conv1
=
nn
.
Sequential
(
nn
.
Conv2d
(
num_channels
,
64
,
kernel_size
=
9
,
padding
=
4
*
int
(
padding
),
padding_mode
=
'replicate'
),
nn
.
ReLU
(
inplace
=
True
))
self
.
conv2
=
nn
.
Sequential
(
nn
.
Conv2d
(
64
,
32
,
kernel_size
=
1
,
padding
=
0
),
# n1 * 1 * 1 * n2
nn
.
ReLU
(
inplace
=
True
))
self
.
conv3
=
nn
.
Conv2d
(
32
,
num_channels
,
kernel_size
=
5
,
padding
=
2
*
int
(
padding
),
padding_mode
=
'replicate'
)
def
forward
(
self
,
x
):
x
=
self
.
conv1
(
x
)
x
=
self
.
conv2
(
x
)
x
=
self
.
conv3
(
x
)
return
x
def
init_weights
(
self
):
for
L
in
self
.
conv1
:
if
isinstance
(
L
,
nn
.
Conv2d
):
L
.
weight
.
data
.
normal_
(
mean
=
0.0
,
std
=
0.001
)
L
.
bias
.
data
.
zero_
()
for
L
in
self
.
conv2
:
if
isinstance
(
L
,
nn
.
Conv2d
):
L
.
weight
.
data
.
normal_
(
mean
=
0.0
,
std
=
0.001
)
L
.
bias
.
data
.
zero_
()
self
.
conv3
.
weight
.
data
.
normal_
(
mean
=
0.0
,
std
=
0.001
)
self
.
conv3
.
bias
.
data
.
zero_
()
細節一: 論文中,網路在訓練時摺積層不進行padding,在測試時進行padding,padding的像質數量為每邊填充 \lfloor f/2 \rfloor ,padding方式為 ‘replicate’ ,如果采用零填充會導致輸出的圖片四周有邊框(boarder effect)。
細節二: 所有摺積層的權重weight使用均值為零,標準差為0.001的正態分布初始化,偏置bias為零。
二、數據集的準備
訓練集: SRCNN的訓練集使用91-images。
1、數據增廣(augment):為了提高模型的泛化能力,對數據集進行了增廣。方法是:將原始圖片先進行 0°、90°、180°、270° 旋轉,然後縮放 0.6、0.7、0.8、0.9、1.0 ,得到20倍於91-images的數據集,共1820張HR圖片。
2、準備LR-HR數據對:
在經過上述處理後最後得到276864對數據對,即每個epoch處理276864對。
細節一: 由於python的PIL庫中的‘bicubic’插值與matlab的‘bicubic’不同,因此需要在python中實作matlab的‘bicubic’插值。本人在網上找到了一個python實作matlab中imresize函式的庫,經過驗證與matlab得到的結果一致。
細節二: 同樣的,matlab中rgb2ycbcr的函式也略有不同,主要是轉換矩陣的值和取整上的差別。以下為python實作的相同效果的轉換函式:
# https://en.wikipedia.org/wiki/YCbCr
m
=
np
.
array
([[
65.481
,
128.553
,
24.966
],
[
-
37.797
,
-
74.203
,
112.0
],
[
112
,
-
93.786
,
-
18.214
]])
def
rgb2ycbcr
(
rgb
):
shape
=
rgb
.
shape
if
len
(
shape
)
==
3
:
rgb
=
rgb
.
reshape
((
shape
[
0
]
*
shape
[
1
],
3
))
ycbcr
=
np
.
dot
(
rgb
,
m
.
transpose
()
/
255.
)
ycbcr
[:,
0
]
+=
16.
ycbcr
[:,
1
:]
+=
128.
ycbcr
=
np
.
round
(
ycbcr
)
return
ycbcr
.
reshape
(
shape
)
def
ycbcr2rgb
(
ycbcr
):
shape
=
ycbcr
.
shape
if
len
(
shape
)
==
3
:
ycbcr
=
ycbcr
.
reshape
((
shape
[
0
]
*
shape
[
1
],
3
))
rgb
=
copy
.
deepcopy
(
ycbcr
)
rgb
[:,
0
]
-=
16.
rgb
[:,
1
:]
-=
128.
rgb
=
np
.
dot
(
rgb
,
np
.
linalg
.
inv
(
m
.
transpose
())
*
255.
)
rgb
=
np
.
round
(
rgb
)
return
rgb
.
clip
(
0
,
255
)
.
reshape
(
shape
)
細節三: 轉換為YCbCr時需要註意,如果圖片本身就是灰度圖,只有一個通道,就不需要再轉化,直接將該通道作為Y通道輸入即可。
驗證集: 驗證集使用Set5。
與訓練集的處理相同,但是可以不用裁剪sub-images,直接將完整的圖片作為輸入,這樣驗證的結果更接近實際的測試結果。
測試集: 測試集使用Set5、Set14。測試集的處理將在第四節介紹。
三、模型訓練設定
訓練時一些詳細的參數論文中並沒有提及,因此為了能夠加速訓練結果收斂,一些設定是我自己的經驗,文中使用括弧標註。
訓練的設定如下:
四、測試PSNR
PSNR的計算公式如下:
PSNR=10*log_{10}(\frac{MAX^2}{MSE})=20*log_{10}(\frac{MAX}{\sqrt{MSE}})
其中的 MAX 為像素的取值範圍的最大值,如果影像的像素為 [0,1] ,則MAX=1 ;如果為 [0,255] ,則MAX=255 。
在測試時計算PSNR,按照「江湖規矩」,需要將原始的高畫質圖片 hr 的四個邊緣各裁剪scale個像素。
由於在測試時會進行padding,因此輸出的 sr 與 hr 同尺寸,所以為了計算PSNR,也要對 sr 進行同樣的處理。
由於輸入網路的是Y通道,因此若要得到完整的圖片,需要將輸出的Y通道與輸入前的CbCr組合成完整的YCbCr影像,然後轉換為RGB。若為灰度圖則無需處理。
五、最終結果
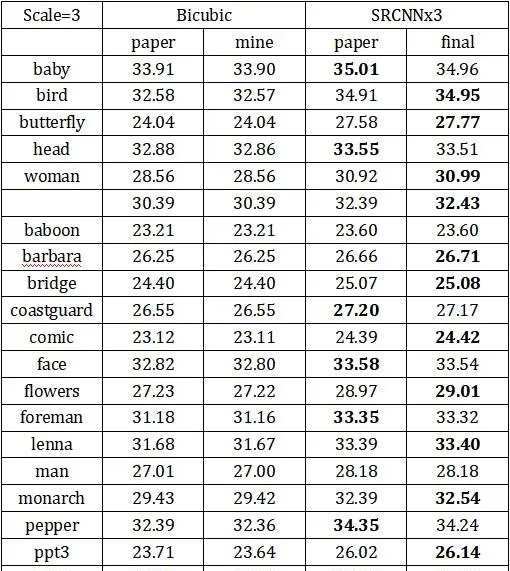
以下結果均為上述設定下,訓練 6000 個 epoch 得到的結果。
在Set5、Set14上測試PSNR:
圖片結果:
















