在之前做最小平方法擬合車道線時,有時發現單線擬合不足以滿足需求,這時候就需要分段線性回歸模型解決該問題。
舉一個簡單的例子,在地球上任意一點溫度(k)隨高度(h)的變化:
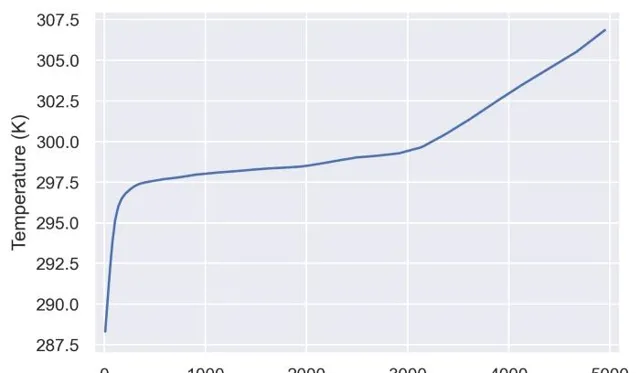
上圖顯示了溫度隨高度(d_{t}/d_{z} )的變化。我們可以看到,溫度的變化不是一條很好的直線。這在分析數據時產生了一些影響。例如,如果我們試圖計算(d_{t}/d_{z} ),它給出的結果並不能準確地代表大氣的不同層(或部份)的變化。
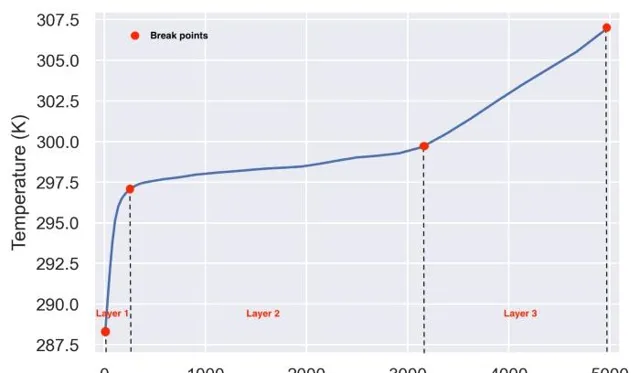
事實上,我們可以將其劃分為3個不同的層(或部份)。上面我們可以看到這些層的表示和它的近似高度(x軸)。斷點是數據完全改變其行為的點,比如曲率斜率變化明顯等。例如,斷點1(表示為b1)是我們的起點;b1和b2之間的層有類似的d_{t}/d_{z} 。但是,當它到達b2時,d_{t}/d_{z} 的變化更加平滑,不再像以前那樣呈指數增長。我們想要了解的是d_{t}/d_{z} 在每一層中是如何變化的,以及斷點在哪裏。
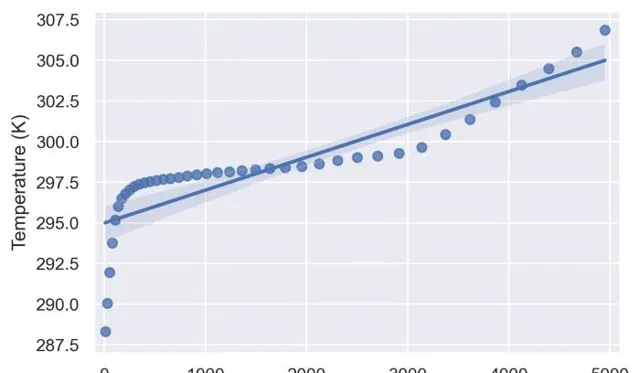
如果我們繪制數據並試圖對其進行回歸,擬合出來的效果就會非常差。然而,這並不意味著線性回歸不是我們問題的最佳選擇,我們稍微調整一下。

上圖繪制了一個擬合數據的三階多項式回歸。多項式回歸的問題是,當添加多項式項(二次的,三次的,等等)時,你失去了模型的可解釋性。但是在不同區間變化比較明顯的情況,三次多項式也不能很好的表達數據,假如用更高階呢?那麽就可能會產生龍格現象,造成更差的結果。可我們換一種想法,可不可以針對特征進行數據分割去做呢?這時候我們就要考慮使用分段線性回歸,其背後的想法是,如果數據在數據的不同區域遵循不同的線性趨勢,如前所示,那麽我們應該「分段」建模回歸函式。下面是構成問題的方程式組:
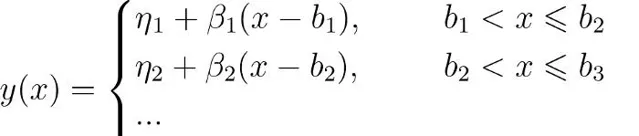
其中b1是第一個斷點的x位置,b2是第二個斷點的x位置,以此類推,直到最後一個斷點 b_{nb} ,總共有nb個斷點。 雖然解決線性回歸相當簡單,但仍然存在一個問題:如何找到斷點?對我來說,這就是我被困的地方。您可以嘗試使用一組for迴圈來強力解決它,但這不是最優的方法。值得慶幸的是,Charles Jekel建立了一個相對簡單和直接的python庫,名為pwlf
import pwlf
import pandas as pd
import numpy as np
#fit your data (x and y)
myPWLF = pwlf.PiecewiseLinFit(df['Height (m)'], df['Temperature (K)'])
#fit the data for n line segments
z = myPWLF.fit(3)
#calculate slopes
slopes = myPWLF.calc_slopes()
# predict for the determined points
xHat = df['Height (m)']
yHat = myPWLF.predict(xHat)
#calculate statistics
p = myPWLF.
se = myPWLF.se # standard errors
只需幾行程式碼,您就可以建立如上所示的分段線性模型。在我的例子中,我知道我需要3個回歸來匹配我的數據,所以我只是透過它,然後透過演算法找到斷點。PWLF演算法是透過差分前進演化演算法尋找給定函式的全域最小值;在我們的例子中,是殘留誤差的平方和。後面我會進一步說一下差分前進演化演算法的本質及用法。
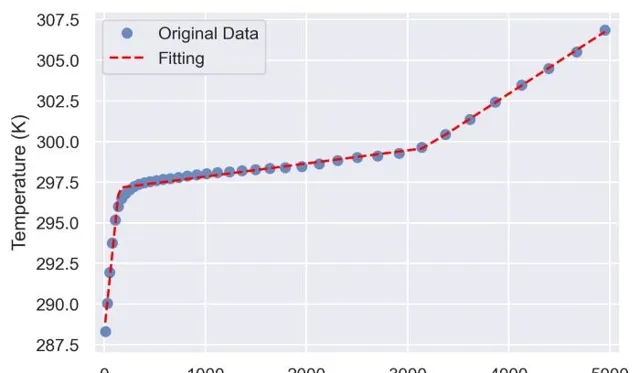
現在已知了斷點,我們就可以擬合數據了。最令人驚奇的是你仍然可以將每個部份作為一個正常的線性回歸來分析,計算與線性回歸相同的統計量,等等。我們可以從上圖中看到pwlf的結果。
分段線性回歸利用了線性回歸的優點,解決了簡單線性回歸無法解決的復雜問題。這個簡單演算法最令人驚嘆的部份是,它可以讓你透過解決多重線性回歸來輕松理解數據,所以如果你的數據不適合單一的直線,分段線性回歸可以幫助你。此外,我們還看到PWLF庫是實作分段線性回歸的一種相當簡單的方法,並且有一種簡單易懂的方法。掌握它可以幫助您對復雜的數據有更多的見解。











