
在數學中,有很多重要的「未解之謎」,最知名的是7個千禧難題,它們是:NP完全問題、霍奇猜想、龐加萊猜想、黎曼假設、楊-米爾斯存在性和品質缺口、納維-斯托克斯方程式、BSD猜想,其中龐加萊猜想已被解決。
龐加萊猜想,拓撲學上的一顆明珠,揭開宇宙形狀之謎
然而,還有其他一些問題也是「價值不菲的」,比如比爾猜想,該問題是本文的重點。比爾是一位著名的銀行家,同時也是一位數學愛好者,他聲稱要為正確解決這個問題的人提供一百萬美元的獎金。
互質
如果兩個整數n和m的最大公因數是1,則它們就是互質的。很明顯,所有一對(不相等的)質數都是互質整數,但例如(9,4)也是互質整數,因為沒有質數能同時整除它們。
猜想
比爾猜想的內容如下:
設
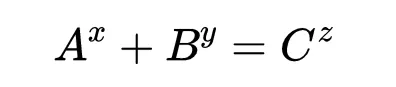
方程式1
其中A,B,C,x,y和z是自然數(正整數)。如果x、y和z都大於2,那麽A、B和C肯定有一個共同的質因數。
下面是這個方程式的例子:
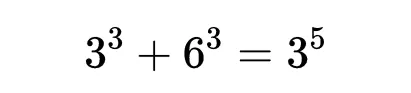
請註意,在這個方程式中,所有三個項都有質數3作為因子,因為3能分別除3、6和3。
理解任何形式的 "如果P那麽Q "命題的一個好方法是考慮與之等價的反命題。反命題的真值和原始命題的真值是一樣的,所以反命題的證明會立即證明原始命題(反之亦然)。
比爾猜想的反命題陳述如下:
假設方程式(1)成立,A,B,C,x,y和z是自然數(正整數)。
如果A、B和C是互質的(即它們不共享一個素因子),那麽x、y或z必須是1或2。
我們可以用比爾猜想的反命題來構造一個方程式,迫使該方程式在A、B和C互質,以及x、y z大於2的情況下為真。然後,該猜想指出,這個方程式沒有自然數的解。
首先,我們需要 貝祖恒等式 :
設a和b是有最大公因數d的整數。那麽存在整數x和y,使得ax + by = d。
貝祖定理的一個推論如下:
設a和b是互質的自然數。那麽存在整數n和m,使得na+mb=1。
請註意,反之亦然,因為如果存在整數n和m,使得na+mb=1,並且a和b不是互質的,那麽它們有一個共同的質因數p,根據質數的定義,這個質因數大於1。這意味著p能除1,這顯然是一個矛盾。因此,a和b是互質的。
現在我們可以說明以下情況:
若且唯若存在整數n和m,使得na+mb=1時,a和b是互質的。
請註意,如果我們知道比爾方程式(1)成立,那麽 "A、B和C不共享一個共同的質因數 "的說法就等同於A和B是互質的說法。
這是因為如果A和B有一個共同的質因數p,那麽我們可以從(1)的左手邊提出這個質因數。這表明,C^z也有p作為質因數。所以如果A和B有一個共同的因子,那麽它們都有這個因子。
這句話的反義是:
如果A、B和C沒有公因數,且方程式(1)成立,則A和B互質。
現在我們可以把兩個方程式結合起來,確保它們都透過平方而成立:
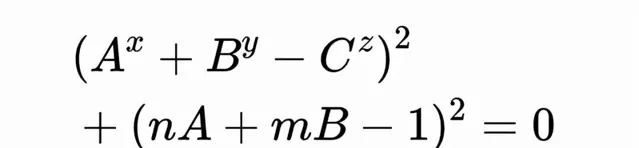
如果這個方程式有自然數x, y, z, A, B, C和整數n, m的解,那麽x, y或z中至少有一個是1或2。
如果你能證明這一點,那麽你將得到一百萬美元。
與費馬最後定理的聯系
要得到一百萬美元並不容易。首先,證明需要發表在AMS認可的同行評議的雜誌上。事實證明,比爾猜想是費馬大定理(FLT)的一個概括。費馬大定理指出,對於n≥3的方程式,沒有自然數解:
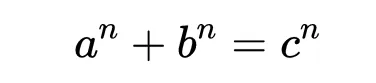
n≥3。
費馬大定理花了數學家350年的時間來證明,而證明過程漫長、復雜,依賴於現代專業數學。事實上,這個證明是如此復雜,以至於這個星球上只有少數人能理解它。
比爾猜想,從任何意義上來說,都比FLT更難。
因此,除非你找到一個完全不同的方法來證明,而這個方法350年來一直被世界上最好的數學家所忽視,否則至少可以說,比爾猜想的證明似乎遙不可及。
為了證明BC(比爾猜想)是FLT(費馬大定理)的推廣,我們需要證明BC => FLT。也就是說,如果比爾猜想是真的,那麽費馬大定理就是真的。
當然,我們知道費馬大定理是正確的,因為上面提到的安德魯·懷爾斯(Andrew Wiles)透過模量定理(Modularity Theorem)的證明。模量定理可以非正式地看作是橢圓曲線世界和模形式世界之間的一座橋梁。
這的確是一個令人震驚的成就。
然而,我們要證明的是,即使我們不知道安德魯的證明,比爾猜想仍會暗示費馬大定理成立。為了看到這一點,我們假設比爾猜想是真的,而且對於自然數a、b、c和一些自然數指數n(n≥3),像上面這樣的費馬方程式是成立的。
然後透過比爾猜想,我們知道a、b和c有一個公因數p,現在我們可以透過p^n來獲得費馬大定理的另一個解。透過繼續除以共質數的n次方,我們最終會得到一個a和b互質的解。
這與比爾猜想的假設相矛盾,因此對於n≥3的情況不可能有這樣的解,即費馬大定理成立。比爾猜想是一個迷人的數位之謎。就像費馬大定理一樣,它吸引我們的原因是其簡單的定義,但正如我們現在所知,外表是具有欺騙性的。











