拉格朗日量 (Lagrangians,簡稱為拉氏量)是一種數學運算式,它包含了一個物理系統中幾乎所有我們關註的資訊。拉氏量通常具有 對稱性 ,這意味著當我們以某種特定方式轉動或移動它們時,它們並不會發生改變。對稱性和拉氏量非常重要,因為我們可以利用它們構造 守恒量 。
守恒量是在整個物理系統演化過程中保持不變的可觀測物理量。
物理學家喜歡尋找守恒量,因為它們不僅具有深刻的哲學意義,還在解方程式過程中非常有用。當你知道有些量保持不變時,用它們可以簡化方程式的求解。
旋轉 這樣 「平滑」的對稱性是 連續對稱性 。 諾特定理 表明,對於每一個連續對稱性,我們都可以構造一個守恒量。例如,如果一個系統具有旋轉對稱性,我們就可以得到角動量守恒 。
更令人驚訝的是,諾特定理可以證明能量守恒是時間平移對稱性的結果,時間平移不變性 意味著拉氏量本身 不顯含時間 。
換句話說,如果物理系統所處的背景不隨時間改變,那麽該系統的總能量將不隨時間改變。

對稱性 的概念在力學、經典和現代物理學中隨處可見。例如,在量子物理學中,量子力學系統的對稱性可以與量子角動量守恒對應。在電子理論中,電子的電荷和自旋守恒 源於電子所遵循的對稱性。
用數學如何詳細描述對稱性起的作用?首先,需要解釋 最小作用量原理 ,以及如果我們知道了拉氏量,我們如何用它來計算場的行為。
作用量和拉氏量
假設有一個粒子或場,在兩個預先確定的時間點 t1 和 t2 之間演化。如果它是一個粒子,我們可以透過繪制一條在空間中延伸的路徑來描繪粒子的演化過程,從時間 t1 開始,到時間 t2 結束。如果它是一個場,我們可以想象一個熱力圖 隨著時間慢慢演化。
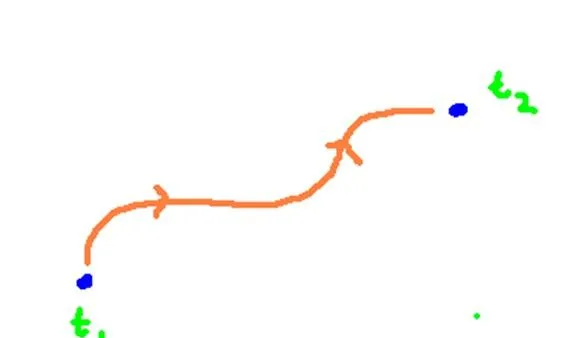
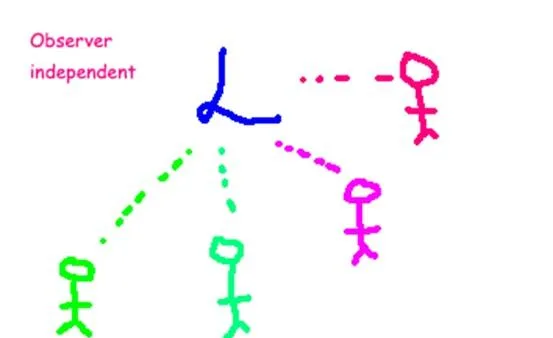
透過這些粒子和場的行為,我們能知道些什麽?我們怎麽才能知道粒子將走什麽路徑?在物理學中,我們從一個可以描述物理系統的模型開始,其中典型的一種是拉氏量。拉氏量是一個數學量,它通常寫成 動能和勢能之差 ,拉氏量在任何時間點都可以給出一個具體的數。我們之所以喜歡用拉氏量是因為它 獨立於觀察者 ,不隨參考系的改變而改變。
觀察者是正立的還是倒立的,或者以接近光速的速度移動,這些都不重要。通常,物理量的數值會因座標選擇的不同而不同;然而,拉氏量不隨座標的選擇而改變,無論對於哪個觀測者,它的取值都是一樣的。和參考系 無關的這種性質是非常有用的,因為它讓我們可以進行清清楚楚的計算。
為了理解到底發生了什麽,我們需要構造一個稱為 作用量(action) 的量。例如,如果已知一個拉氏量,我們可以計算拉氏量在兩個時間點之間的 積分 :

積分意味著將拉氏量在多個時間點上的值進行相加。從t1 到t2之間的總積分被稱為作用量。它通常用大寫字母 S 表示。拉氏量前面的豎直曲線 ∫ 表示積分。
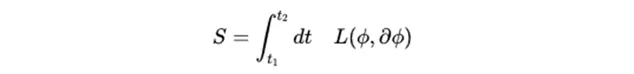
上面的運算式是作用量的數學定義。拉氏量通常是位置和位置的 一階導數 的函式 。希臘字母 φ 表示粒子在空間中的位置;第二項 ∂φ 是粒子位置的一階導數,表示粒子位置隨時間的 變化率 。
拉氏量 在幾何上看起來是怎麽樣的?我們可以用一些插圖來說明,透過這些插圖可以了解關於它的一般概念。如果拉氏量只包含自由空間中的動能,對於不同於直線的路徑,往往會得到更大的作用量。該圖顯示了粒子在時間t1和t2之間采取不同路徑對應的作用量大小。正如您所看到的, 最復雜的路徑作用量最大 。作用量最小的路徑就是直路線徑。

如何得出物理規律?
在我們眼中,拉氏量是數學物件,我們只把 作用量 看作是物理的。這有一個哲學上的原因。結果表明,不同的拉氏量可以產生相同的作用量。所以,在某些情況下,存在兩個拉氏量,但只有一個作用量的情況。這意味著我們可以透過兩個不同的拉氏量,得出相同的物理定律 。
為什麽會這樣?原因是,當我們對某些被稱為「 全微分 」(total derivative)的數學運算式進行積分時,積分結果是零。
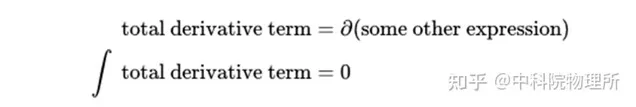
在下面的公式中,我們有一個作用量,被寫成一個特定的拉氏量和一個全微分項。但是,我們可以把積分拆分成兩個不同的部份。一旦我們把它分開,我們就消掉了全微分項,因為當我們積分時它變成了零。
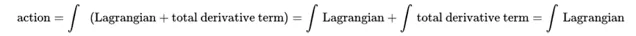
這是一件令人興奮的事情!這意味著,存在兩個不同的拉氏量,在一個不那麽嚴格的限制下,可以認為它們是「等價」的。我們不需要讓它們完全等價就能得出相同的物理現象。如果拉氏量僅在「全微分」項上存在差異,則它們可以被看作是相互等價的。例如,在下圖中,函式 f 、 g 和 h 都與全微分項有關,它們三個產生相同的作用量。(我已經用不同的顏色寫出了這三個函式來表達這個觀點。)
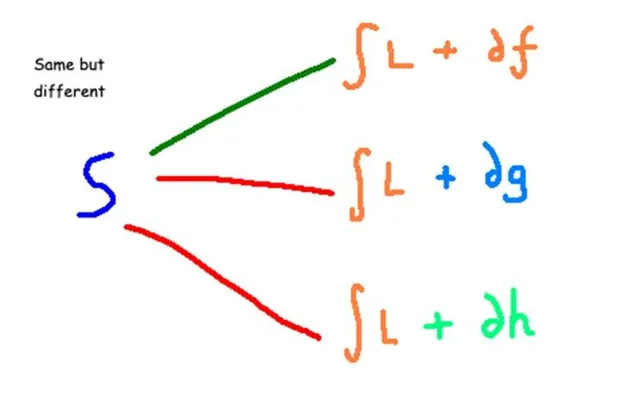
數學上,我們可以用下面的運算式來表達拉氏量之間「等價」,盡管它們之間相差一個全微分項。在下面的運算式中,函式 f 是 可微函式 。
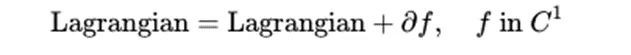
如果對函式可以使用「變化率」的概念,那麽這個函式就是可微的。如果函式值在某些地方發生跳躍、出現尖銳的拐點或沒有 良定義 ,那麽就有可能不能使用「變化率」的概念,這種情況下,只有許多嚴格的數學條件被滿足時,「變化率」的概念才變得可以接受。所有可微函式的集合為C¹。關於微分和積分 等運算是否具有良定義的研究稱為數學分析,是一個令人著迷的研究領域。
歐拉-拉格朗日公式
「最小作用量原理 」告訴我們,場或粒子的行為正是使作用量取 極小值 的行為。所以如果我們知道這個作用量,我們可以透過一些數學運算,求出使這個作用量取極小值時場的行為。有一個被稱為 變分法 的數學分支,研究的是「函式的變化率」。(譯者註:變分法告訴我們,場或粒子的行為可以用歐拉-拉格朗日方程式匯出。)
粒子版的歐拉-拉格朗日方程式如下所示。方程式左邊,我們首先取拉氏量對速度的偏導數 ,然後繼續對其求時間的導數。方程式右邊,我們對拉氏量在空間中進行求導。然後讓方程式的左邊等於右邊,就可以得到一個令作用量取最小值的路徑。
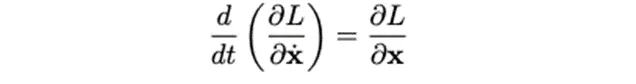
場論版的歐拉-拉格朗日方程式 和粒子版的很相似,方程式如下所示:
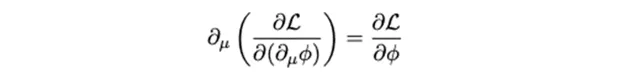
它可以給出場在時空中的 演化方式 。
以下為譯者註:
守恒量
前面我們介紹可以用對稱性匯出守恒量,接下來我們將介紹如何做到這一點。諾特定理告訴我們,每個對稱性對應一個守恒量。
如果物理系統具有時間平移不變性,也就是說拉氏量不顯含時間,那麽可以得到運算式:
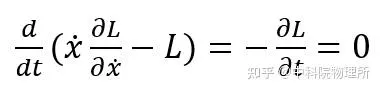
等式左側的括弧裏就是能量(哈密頓量 ),它隨時間的導數是零恰恰表明它不隨時間改變。
如果物理系統具有空間平移不變性,也就是說拉氏量不顯含空間座標,那麽可以得到運算式:
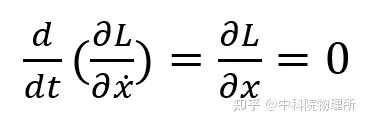
等式左側括弧內正是(共軛)動量,它不隨時間改變,這就是 動量守恒 。
作者:Afiq Hatta
轉譯:Nothing
審校:Zhenni
原文連結:
https://www. cantorsparadise.com/noe thers-theorem-and-the-principle-of-least-action-c84b789c51b6











