CAE工程師一名,最近在復習材料力學,正好回答這個問題。
高贊的各位寫得都很專業,但個人認為 @蒙特遇見卡羅 的觀點最為簡單明了。
若彈性模量影響系統剛度分配,則應力結果與彈性模量有關,比如靜不定問題;若彈性模量不影響系統剛度分析,則應力結果與彈性模量無關,比如單個試件單軸拉伸實驗。
我們首先來看拉壓、彎曲、扭轉和組合工況中,應力與彈性模量是否有關。
1、哪些情況應力與彈性模量無關?
1.1 單軸拉伸工況
單軸拉伸工況,兩個試件左端固定約束,右端施加相同大小的力使試件產生拉伸變形,彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量不同,但應力完全相同 。
單軸拉伸時,應力計算公式為 \sigma=\frac{F}{A} ,F為拉力,A為截面積,應力與彈性模量完全無關。

1.2 彎曲工況
彎曲工況中,兩個試件左端固定約束,右端施加相同大小的力使試件產生彎曲變形,兩個試件彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量不同,但應力完全相同 。
純彎曲時,梁截面上正應力計算公式為 \sigma=\frac{My}{I_z}=\frac{My}{\int_{}^{}y^2dA} , M 彎矩,y為與中性面距離,A為面積,應力與彈性模量完全無關。

1.3 扭轉工況
扭轉工況,兩個試件左端固定約束,右端施加相同大小的扭矩使試件發生扭轉變形,兩個試件彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量不同,但應力完全相同 。
純彎曲時,圓柱截面上切應力計算公式為 \tau_{max}=\frac{TR}{I_p}=\frac{TR}{\int_{A}^{}\rho^2dA} ,T為扭矩,R為圓柱半徑,應力與彈性模量完全無關。
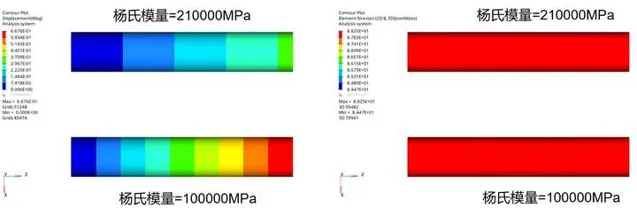
1.4 組合變形工況
拉伸+彎曲+扭轉組合工況下,兩個試件,左端固定約束,右端施加相同大小的扭矩+拉力+彎力使試件發生組合變形,兩個試件彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量不同,但應力完全相同 。
由以上內容可知,對於單個零件而言,拉伸、彎曲、扭轉以及組合工況下,應力結果與彈性模量無關。
2、哪些情況應力與彈性模量有關?
2.1 位移載入
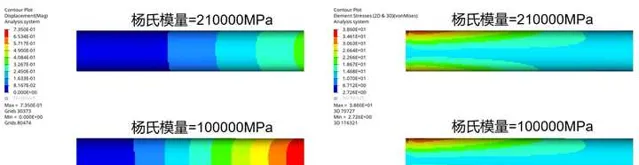
單軸拉伸工況,兩個試件左端固定約束,右端施加相同大小的強制位移載荷,兩個試件彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量相同,但應力不同,此時應力與彈性模量有關 。

2.2 大變形工況
大變形工況下,兩個試件左端固定約束,右端施加相同大小的集中力載荷,兩個試件彈性模量分別取210GPa和100GPa,由下圖可知,兩個試件 變形量不同,應力也不同,此時應力與彈性模量有關。
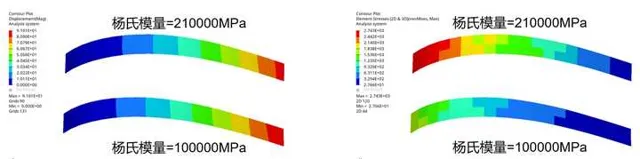
2.3 靜不定問題
如下所示靜不定問題,桿1、桿2和桿3為材料相同半徑相同的圓桿,加入變形協調方程式可求得桿1、桿2和桿3的受力大小分別為 F_{N1}=F_{N2}=\frac{Fcos^2\alpha}{2cos^2\alpha+\frac{E_3A_3}{E_1A_1}} , F_{N3}=\frac{F}{1+2\frac{E_1A_1}{E_3A_3}cos^3\alpha} 。
軸力不同,根據 \sigma=\frac{F}{A} 可知,三根桿上應力也不同,此時彈性模量會影響系統剛度分布,從而影響載荷分配,最後導致應力不同,此時應力與彈性模量有關。
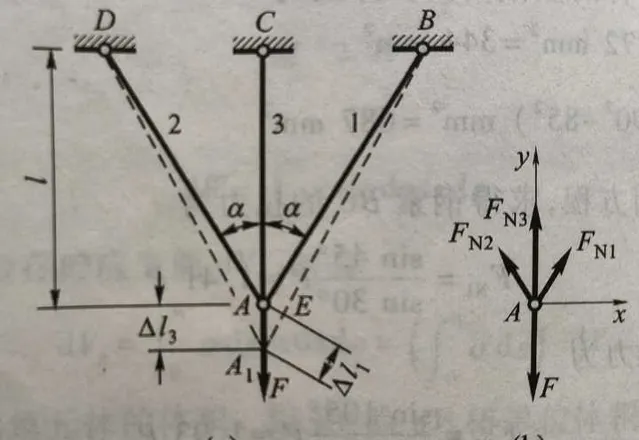
實際工程套用中,多數結構都是越靜定結構,其載荷分配都與彈性模量有關,因此多數實際結構中,應力結果都與彈性模量有關。
結論如下:
裝配體中,彈性模量影響系統中剛度分配,剛度分配決定傳遞載荷大小,載荷大小影響應力;
若彈性模量不影響系統中各零件的剛度比值,則彈性模量不影響應力大小,比如材料力學中的單個零件簡單的拉壓、彎曲、扭轉和剪下四種基本變形;
若彈性模量影響系統中每個零件的剛度比值,則彈性模量影響應力大小,比如絕大多數靜不定工況。
我的上一篇文章中寫到了焊縫/焊點區域應力計算不準確問題,應力不準確的原因可以用上面的結論來解釋。
點焊和縫焊過程中,焊接區域的高溫會影響周圍熱影響區的材料效能參數,其彈性模量會發生改變;對於裝配體,單個部件某個區域的彈性模量改變會影響整個系統的剛度分配,從而導致整個模型中載荷分配發生變化,最終會導致焊接區和熱影響區應力發生改變;
焊接仿真目前最大的問題在於無法獲得熱影響區準確的材料參數,因此無法得到焊接區域準確的應力分布。
碼字不易,點個贊吧,更多有限元相關硬核分享,請點選頭像,檢視我的主頁 @熊庫辛












