前三部份引路:
(收個尾,可能這是最後一部份了QAQ)
Last. xyz約定(姿態角,"xyz convention")
這一種約定在研究飛機運動姿態時常用,而且對應的歐拉角也有自己的名稱。
為更加形象,引入一張飛機的圖片:
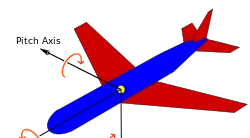
同樣,旋轉分為三步:
(1) 繞 z 軸轉動 \phi 角;
(2) 繞第一次轉動後的 y 軸轉動 \theta 角(按慣例,該角 順時針 為正,若嚴格按逆時針為正的話應為轉動-\theta 角);
(3) 繞第二次轉動後的 x 軸轉動 \psi 角。
其中, \phi 稱為 偏航角(yaw angle) ,\theta 稱為 俯仰角(pitch angle) , \psi 稱為 滾轉角 (roll angle) 。
在上面的圖中可以清晰看出這三個角的含義。
然後自然可以寫出三步旋轉的矩陣:
\bm{D}=\begin{pmatrix} \cos\phi &\sin\phi & \\ -\sin\phi & \cos\phi & \\ & & 1 \end{pmatrix}, \bm{C}=\begin{pmatrix} \cos\theta & & -\sin\theta\\ & 1 & \\ \sin\theta & & \cos\theta \end{pmatrix},\bm{B}=\begin{pmatrix} 1 & &\\ &\cos\psi &\sin\psi \\ &-\sin\psi & \cos\psi \\ \end{pmatrix}
以及合矩陣:
\bm{A}=\bm{B}\bm{C}\bm{D}=\begin{pmatrix} \cos\theta\cos\phi & \cos\theta\sin\phi & -\sin\theta\\ -\cos\psi\sin\phi+\sin\psi\sin\theta\cos\phi & \cos\psi\cos\phi+\sin\psi\sin\theta\sin\phi & \cos\theta\sin\psi\\ \sin\psi\sin\theta+\cos\psi\sin\theta\cos\phi & -\sin\psi\cos\phi+\cos\psi\sin\theta\sin\phi & \cos\theta\cos\psi \end{pmatrix}
還有 \bm{Q} 矩陣:
\begin{aligned} \bm{Q}&=\begin{pmatrix} \cos\dfrac{\psi}2& i\sin\dfrac{\psi}2\\ i\sin\dfrac{\psi}2& \cos\dfrac{\psi}2 \end{pmatrix}\begin{pmatrix} \cos\dfrac{\theta}2& \sin\dfrac{\theta}2\\ - \sin\dfrac{\theta}2& \cos\dfrac{\theta}2 \end{pmatrix}\begin{pmatrix} e^{i\frac{\phi}2} & \\ & e^{-i\frac{\phi}2} \end{pmatrix}\\ &=\begin{pmatrix} \left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{i\frac{\phi}2} & \left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \\ -\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{i\frac{\phi}2} & \left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \end{pmatrix}\end{aligned}
從中得到Cayley-Klein參量和Euler參量
\begin{cases} \alpha=\left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{i\frac{\phi}2}\\ \beta=\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{-i\frac{\phi}2}\\ \gamma=-\left( \cos\dfrac{\psi}2\sin\dfrac{\theta}{2}-i\sin\dfrac{\psi}2\cos\dfrac{\theta}2\right)e^{i\frac{\phi}2}\\ \delta=\left( \cos\dfrac{\psi}2\cos\dfrac{\theta}{2}+i\sin\dfrac{\psi}2\sin\dfrac{\theta}2\right)e^{-i\frac{\phi}2} \end{cases}
\begin{cases} e_0=\cos\dfrac{\psi}2\cos\dfrac{\theta}2\cos\dfrac{\phi}2+\sin\dfrac{\psi}2\sin\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_1=\sin\dfrac{\psi}2\cos\dfrac{\theta}2\cos\dfrac{\phi}2-\cos\dfrac{\psi}2\sin\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_2=\cos\dfrac{\psi}2\sin\dfrac{\theta}2\cos\dfrac{\phi}2+\sin\dfrac{\psi}2\cos\dfrac{\theta}2\sin\dfrac{\phi}2\\ e_3=-\sin\dfrac{\psi}2\sin\dfrac{\theta}2\cos\dfrac{\phi}2+\cos\dfrac{\psi}2\cos\dfrac{\theta}2\sin\dfrac{\phi}2 \end{cases}
再考慮角速度變換。不難看出, \dot\phi 在空間 z 軸方向, \dot\theta 在第一次轉動的後 y 軸方向, \dot\psi 在第二次轉動後的x軸方向。從而不難寫出角速度向量的兩種形式
在剛體座標系 Ox'y'z' 下:
\begin{aligned} \bm{\omega}&=\bm{BCD}\begin{pmatrix} 0\\0\\1 \end{pmatrix}\dot\phi+\bm{B}\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\ &=\begin{pmatrix} \dot\psi-\dot\phi\sin\theta\\ \dot\theta\cos\psi+\dot\phi\cos\theta\sin\psi\\ -\dot\theta\sin\psi+\dot\phi\cos\theta\cos\psi \end{pmatrix} \end{aligned}
對於空間座標系 Oxyz 下的角速度向量,由於旋轉過程的逆向過程分別是繞x,y,z軸,與原過程不一致,故仍需要用矩陣計算:
\begin{aligned} \bm{\omega}&=\begin{pmatrix} 0\\0\\1 \end{pmatrix}\dot\phi+\bm{B}^{-1}\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+(\bm{BC})^{-1}\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\ &=\dot\phi+\bm{B}^T\begin{pmatrix} 0\\1\\0\end{pmatrix}\dot{\theta}+\bm{C}^T\bm{B}^T\begin{pmatrix} 1\\0\\0\end{pmatrix}\dot\psi\\\\ &=\begin{pmatrix} \psi\cos\theta\cos\phi-\dot\theta\sin\phi\\ \dot\psi\cos\theta\sin\phi+\dot\theta\cos\phi\\ \dot\phi-\dot\psi\sin\theta \end{pmatrix} \end{aligned}