\color{red}{\underline{\overline{\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar}}}
本文點贊破 1w ,後期出一期關於 Stokes 定理的。
\color{red}{\underline{\overline{\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar\quad\bigstar}}}
什麽是向量場?
得得得,不整名詞不整名詞,直接看例子。首先揪出平面上的任意一個點 (x,y) ,然後它在「魔法」 \vec{f} 的作用下變成點 (x-y,x+y) 。下面不妨令 (x,y) 為幾個特殊點,然後我們來看看它們在 f 的作用下變成了啥。

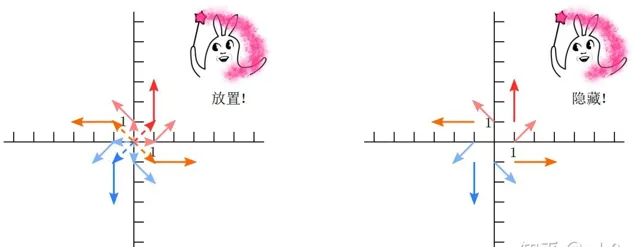
如圖片 1 所示,我們所選的九個特殊點 (x,y),\quad x,\,y=0,\pm1 在「魔法」 \vec{f} 的作用下從左圖變到了右圖。
例如 (x,y)=(1,1) 在「魔法」 \vec{f} 變成了 (x-y,x+y)=(1-1,1+1)=(0,2) 。那麽如果我們將除了原點以外的八個點都視為平面向量會怎樣呢?這樣做的話會產生圖片 2 中的效果:

然後我們將施加了「魔法」的向量與原來的向量放在一起,但是選擇的放置方式是特殊的:將所有施加了「魔法」的向量的起點與之前對應的沒有施加「魔法」的向量的終點放在一起,之所以這樣放置是為了明確對應向量施加「魔法」前後的變化。然後把所有沒有施加「魔法」的向量藏起來可以得到圖片 3 :
如果你選擇充分多的特殊點,然後耐心的繪制它們在「魔法」 \vec{f} 作用下的結果,則最終可以得到圖片 4 [2] :

一言以蔽之,平面向量 \begin{pmatrix} x\\y \end{pmatrix} 在「魔法」 \vec{f} 的作用下變成了平面向量 \begin{pmatrix} x-y\\x+y \end{pmatrix} ,則我們將:
\vec{f}:\mathbb{R}^2\to\mathbb{R}^2:\quad \begin{pmatrix} x\\y \end{pmatrix}\mapsto \vec{f}\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} x-y\\x+y \end{pmatrix}\tag{1.1}
稱為一個 平面向量場 。從式 (1.1) 中我們可以觀察到的平面向量場的特點是什麽呢?它有兩個十分顯著的特點:
- 平面向量場 \vec{f} 是從平面到平面上的對映;
- 平面向量場 \vec{f} 有兩個分量。
整幾個例子 look look?
平面向量場自然是豐富多彩的,比如這樣的:

\vec{f}:\mathbb{R}^2\to\mathbb{R}^2:\quad \begin{pmatrix} x\\y \end{pmatrix}\mapsto \vec{f}\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} \sin(x)\\ \cos(y) \end{pmatrix}\tag{1.2}
這樣的:
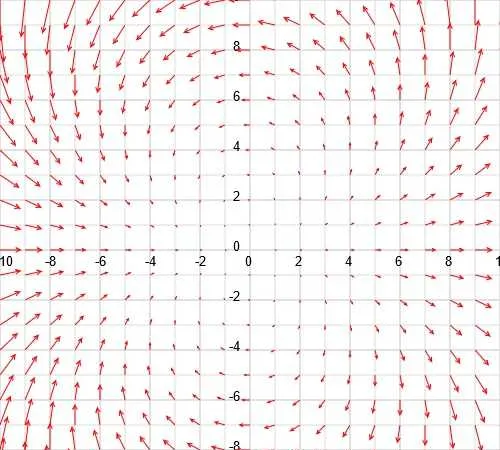
\vec{f}:\mathbb{R}^2\to\mathbb{R}^2:\quad \begin{pmatrix} x\\y \end{pmatrix}\mapsto \vec{f}\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} x^2-y^2\\ 2\cdot x\cdot y \end{pmatrix}\tag{1.3}
還有這樣的:

\vec{f}:\mathbb{R}^2\to\mathbb{R}^2:\quad \begin{pmatrix} x\\y \end{pmatrix}\mapsto \vec{f}\begin{pmatrix} x\\y \end{pmatrix}=\begin{pmatrix} \sin(x+y)\\ \cos(x+y) \end{pmatrix}\tag{1.4}
好看吧?好看的話就先擦擦口水,然後我們繼續。
深入探討一下?
光擦口水不行啊,美好的事物那不得深入了解一下?

哦?散度?

啊~被一箭穿心了。但是可惜,射歪了。有效愛意只有短短的淺玫瑰紅那一部份。現在調整 角度 ,來再(補)射(充)一(愛)箭(意)

看,有效愛意增加了吧。行了,美夢可以醒了,起床學習了。不過誰說這只是一場夢啊,嗯?我能用它解釋散度你信嗎?

我要開始了啊。
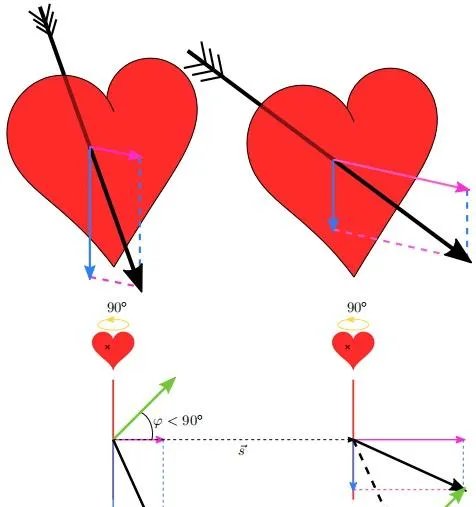
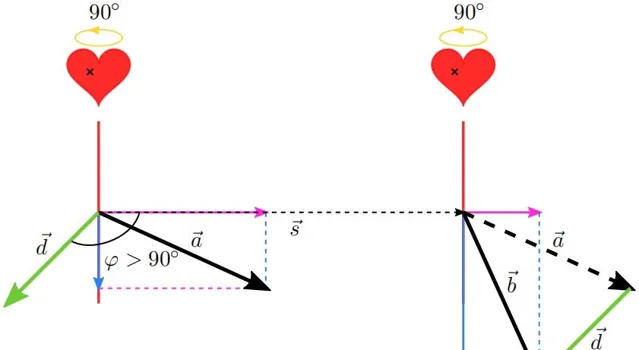
首先將兩次「打靶」的結果豎直放置,並且讓它們處於同一高度上,同時給它們之間留出一些距離 \left|\vec{s}\right| 。然後將它們一起逆時針旋轉 90^{\circ} ,並添加必要的元素,得到圖片 8 。在圖片 8 的下方,我們將所有的箭頭都視為向量。現在我們假設兩次愛意向同一個點發射(圖片 8 中的小叉叉),進而由前述擺放條件可知補充愛意後的入射點位於補充愛意前的入射點水平平移向量 \vec{s} 的位置上。現在我們將左邊箭矢的起點與右邊箭矢的起點移動到一起,然後我們用右邊箭矢所對應的向量減去左邊箭矢所對應的向量,這樣得到的是圖片 8 中綠色的向量。然後我們再將綠色的這個向量移回到補充愛意之前的入射點處。我們發現這個綠色的向量與向量 \vec{s} 之間的夾角小於 90^{\circ} 。
噗。。。說了一大堆,就得到這樣一個結論?那怎麽可能,這只是最表層的結論。等等,忘了個事,繼續之前,我們需要為圖片 8 中的向量們起好名字。它們的名字我都寫在圖片 9 裏面啦:
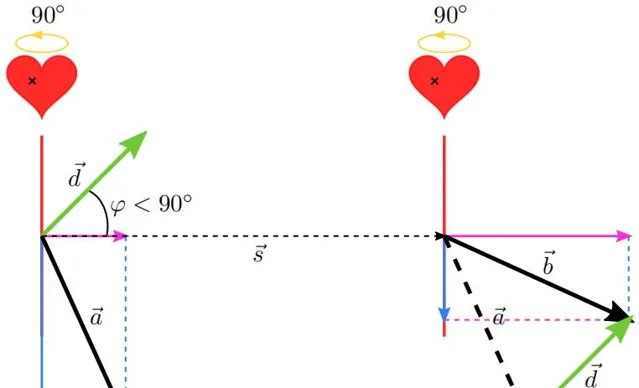
言歸正傳,兩個向量之間的夾角小於 90^{\circ} ,說明這兩個向量的純量積為正呀!即:
\vec{d}\cdot \vec{s}=\left(\vec{b}-\vec{a}\right)\cdot\vec{s}=\vec{b}\cdot \vec{s}-\vec{a}\cdot \vec{s}>0.\tag{2.1}
這又能說明啥呢?這說明了: 向量 \vec{d} 在向量 \vec{s} 方向上的投影與向量 \vec{s} 的方向一致呀! 也就是說, 調整角度之後,沿著向量 \vec{s} 方向的愛意(即有效愛意)增加了呀 ~
如果交換向量 \vec{a} 與向量 \vec{b} 的角色,那麽可惜,此時 沿著向量 \vec{s} 方向的愛意就減少了 。如圖片 10 所示。
現在我們可以把之前的美夢徹底忘掉了,因為我們已經從中得到了初步的結論。下面我們要做稍微抽象一點的工作了。要計算了嗎?不,還早呢。
揉揉眼,現在我們要回到平面上來啦。作為過渡,我們先來簡單的抽象化一下剛才的結論:
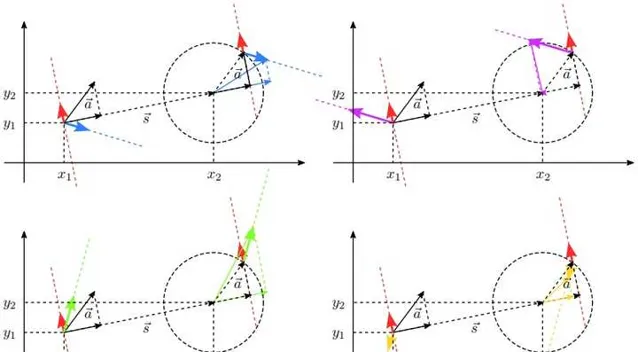
在圖片 11 中,向量 \vec{a} 為點 (x_1,y_1) 所對應的向量(可以將其視為某平面向量場 \vec{f}(x,y) 在點 (x_1,y_1) 的值),而點點 (x_2,y_2) 所對應的向量(可以將其視為同一個平面向量場 \vec{f}(x,y) 在點 (x_2,y_2) 的值)卻不盡相同。
下面我們要來搞點計算了(說是搞計算,實則「瞎扯淡」)。別走,都是簡單的「扯淡」。

在圖片 12 中, \vec{f}(x_0,y_0) 表示的是向量場在點 (x_0,y_0) 對應的值,且 \vec{f}(x_0+\Delta x,y_0) 表示的是向量場在點 (x_0+\Delta x,y_0) 對應的值。現在我們想知道向量 \vec{f}(x_0,y_0) 裏到底有多少部份真正透過了線段 a ,而向量 \vec{f}(x_0+\Delta x,y_0) 裏到底又有多少部份真正透過了線段 b 。

這一點其實比較明顯,如果我們將向量 \vec{f}(x_0,y_0) 與向量 \vec{f}(x_0+\Delta x,y_0) 分別沿著豎直方向與水平方向進行分解的話會發現,向量 \vec{f}(x_0,y_0) 真正透過線段 a 的部份只有紫色分量(水平分量),同理,向量 \vec{f}(x_0+\Delta x,y_0) 真正透過線段 b 的部份只有橙色分量(水平分量),而綠色分量和黃色分量分別被線段 a 和線段 b 「吸收了」。
在進一步之前,我們不妨先設平面向量 \vec{f}(x_0,y_0) 與 \vec{f}(x_0+\Delta x,y_0) 分別為:
\vec{f}(x_0,y_0) :=\begin{pmatrix} f_{x}(x_0,y_0) \\ f_{y}(x_0,y_0) \end{pmatrix},\quad \vec{f}(x_0+\Delta x,y_0) :=\begin{pmatrix} f_{x}(x_0+\Delta x,y_0) \\ f_{y}(x_0+\Delta x,y_0) \end{pmatrix}.\tag{2.2}
現在我們來做一件事,將平面向量 \vec{f}(x_0,y_0) 與 \vec{f}(x_0+\Delta x,y_0) 的水平分量 f_{x}(x_0+\Delta x,y_0) 與 f_{x}(x_0,y_0) 都乘以線段 a (或線段 b )的長度 \Delta y ,然後再做差:
f_{x}(x_0+\Delta x,y_0)\cdot\Delta y-f_{x}(x_0,y_0)\cdot\Delta y=\left(f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)\right)\cdot\Delta y\tag{2.3}.
然後我們給式 (2.3) 補上一個 \Delta x\ne 0 ,即:
\left(f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)\right)\cdot\Delta y=\frac{f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)}{\Delta x}\cdot\Delta x\cdot\Delta y \tag{2.4}.
我們將 \left(f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)\right)\cdot\Delta y 定義為: 水平方向上高度為 y_0 處的流出量 。顯然,在式 (2.4) 中 \Delta x\cdot\Delta y 表示的是矩形圖片 12 中以 \Delta x 為長,\Delta y 為寬的矩形的面積,我們給它起一個新的名字: \Delta x\cdot\Delta y :=\Delta A 。
好,暫時打住。我們先回過頭來研究一下式 (2.4) 。對於這個式子,我們可以分為以下三種情況進行討論:
-
f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)>0
根據之前我們得到的初步結論可推得,這種情況下向量 \vec{f}(x_0+\Delta x,y_0) 在水平方向上的投影做的是正的貢獻。也就是說這種情況下成立:
f_{x}(x_0+\Delta x,y_0)\cdot\Delta y>f_{x}(x_0,y_0)\cdot\Delta y.\tag{2.5}
這說明了水平方向上的高度 y_0 處的流出量為正。
-
f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)<0
根據之前我們得到的初步結論可推得,這種情況下向量 \vec{f}(x_0+\Delta x,y_0) 在水平方向上的投影做的是負的貢獻。也就是說這種情況下成立:
f_{x}(x_0+\Delta x,y_0)\cdot\Delta y<f_{x}(x_0,y_0)\cdot\Delta y.\tag{2.6}
這說明了水平方向上的高度 y_0 處的流出量為負。
-
f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)=0
這種情況下向量 \vec{f}(x_0+\Delta x,y_0) 在水平方向上的投影做的是零貢獻。也就是說這種情況下成立:
f_{x}(x_0+\Delta x,y_0)\cdot\Delta y=f_{x}(x_0,y_0)\cdot\Delta y.\tag{2.7}
這說明了水平方向上的高度 y_0 處的流出量為零。
現在我們來搞搞 y 方向上的計算。

在圖片 13 中, \vec{f}(x_0,y_0) 表示的是向量場在點 (x_0,y_0) 對應的值,且 \vec{f}(x_0,y_0+\Delta y) 表示的是向量場在點 (x_0,y_0+\Delta y) 對應的值。現在跟之前的情況就有所不同了,如果我們將向量 \vec{f}(x_0,y_0) 與向量 \vec{f}(x_0,y_0+\Delta y) 分別沿著豎直方向與水平方向進行分解的話會發現,向量 \vec{f}(x_0,y_0) 真正透過線段 a 的部份只有綠色分量(豎直分量),同理,向量 \vec{f}(x_0,y_0+\Delta y) 真正透過線段 b 的部份只有黃色分量(豎直分量),而紫色分量和橙色分量分別被線段 a 和線段 b 「吸收了」。
在進一步之前,我們不妨先設平面向量 \vec{f}(x_0,y_0) 與 \vec{f}(x_0,y_0+\Delta y) 分別為:
\vec{f}(x_0,y_0) :=\begin{pmatrix} f_{x}(x_0,y_0) \\ f_{y}(x_0,y_0) \end{pmatrix},\quad \vec{f}(x_0,y_0+\Delta y) :=\begin{pmatrix} f_{x}(x_0,y_0+\Delta y) \\ f_{y}(x_0,y_0+\Delta y) \end{pmatrix}.\tag{2.8}
現在我們來做一件事,將平面向量 \vec{f}(x_0,y_0) 與 \vec{f}(x_0,y_0+\Delta y) 的豎直分量 f_{y}(x_0,y_0+\Delta y) 與 f_{y}(x_0,y_0) 都乘以線段 a (或線段 b )的長度 \Delta x ,然後再做差:
f_{y}(x_0,y_0+\Delta y) \cdot\Delta x-f_{y}(x_0,y_0)\cdot\Delta x=\left(f_{y}(x_0,y_0+\Delta y) -f_{y}(x_0,y_0)\right)\cdot\Delta x\tag{2.9}.
然後我們給式 (2.3) 補上一個 \Delta x\ne 0 ,即:
\left(f_{y}(x_0,y_0+\Delta y) -f_{y}(x_0,y_0)\right)\cdot\Delta x=\frac{f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)}{\Delta y}\cdot\Delta x\cdot\Delta y \tag{2.10}.
我們將 \left(f_{x}(x_0,y_0+\Delta y) -f_{x}(x_0,y_0)\right)\cdot\Delta x 定義為: 豎直方向上水平為 x_0 處的流出量 。同理, \Delta x\cdot\Delta y :=\Delta A 。
我們還是回過頭來研究一下式 (2.10) 。對於這個式子,我們可以分為以下三種情況進行討論:
-
f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)>0
根據之前我們得到的初步結論可推得,這種情況下向量 \vec{f}(x_0,y_0+\Delta y) 在豎直方向上的投影做的是正的貢獻。也就是說這種情況下成立:
f_{y}(x_0,y_0+\Delta y)\cdot\Delta x>f_{y}(x_0,y_0)\cdot\Delta x.\tag{2.11}
這說明了豎直方向上水平為 x_0 處的流出量為正。
-
f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)<0
根據之前我們得到的初步結論可推得,這種情況下向量 \vec{f}(x_0,y_0+\Delta y) 在豎直方向上的投影做的是負的貢獻。也就是說這種情況下成立:
f_{y}(x_0,y_0+\Delta y)\cdot\Delta x<f_{y}(x_0,y_0)\cdot\Delta x.\tag{2.12}
這說明了豎直方向上水平為 x_0 處的流出量為負。
-
f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)=0
這種情況下向量 \vec{f}(x_0,y_0+\Delta y) 在豎直方向上的投影做的是零貢獻。也就是說這種情況下成立:
f_{y}(x_0,y_0+\Delta y)\cdot\Delta x=f_{y}(x_0,y_0)\cdot\Delta x.\tag{2.13}
這說明了豎直方向上水平為 x_0 處的流出量為零。
現在兩個方向上的計算以及相應的討論都做完了,下面該幹啥了呀?現在我們還是看回式 (2.4) 與式 (2.10) ,不過這次我們只看兩者的右半邊。當然光看啥也看不出來,我們 xue 微做一下處理:
\frac{f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)}{\Delta x}\cdot\Delta x\cdot\Delta y =\left(\left(f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)\right)\cdot\Delta x\right)\cdot\frac{\Delta y}{\Delta x}\tag{2.14}.
\frac{f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)}{\Delta y}\cdot\Delta x\cdot\Delta y =\left(\left(f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)\right)\cdot\Delta y\right)\cdot\frac{\Delta x}{\Delta y}\tag{2.15}.
變形之後有啥好處呢?好處就是出現了純量積:
\begin{array}{ll} & \display style{\left(f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)\right)\cdot\Delta x} \\ =& \display style{f_{x}(x_0+\Delta x,y_0)\cdot\Delta x-f_{x}(x_0,y_0)\cdot\Delta x} \\ =& \display style{\begin{pmatrix} f_x(x_0+\Delta x,y_0)\\ f_y(x_0+\Delta x,y_0) \end{pmatrix}\cdot\begin{pmatrix} \Delta x\\ 0 \end{pmatrix}-\begin{pmatrix} f_x(x_0,y_0)\\ f_y(x_0,y_0) \end{pmatrix}\cdot\begin{pmatrix} \Delta x\\ 0 \end{pmatrix}} \end{array}\tag{2.16}
以及:
\begin{array}{ll} & \display style{\left(f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)\right)\cdot\Delta y} \\ =& \display style{f_{y}(x_0,y_0+\Delta y)\cdot\Delta y-f_{x}(x_0,y_0)\cdot\Delta y} \\ =& \display style{\begin{pmatrix} f_x(x_0,y_0+\Delta y)\\ f_y(x_0,y_0+\Delta y) \end{pmatrix}\cdot\begin{pmatrix} 0\\ \Delta y \end{pmatrix}-\begin{pmatrix} f_x(x_0,y_0)\\ f_y(x_0,y_0) \end{pmatrix}\cdot\begin{pmatrix} 0\\ \Delta y \end{pmatrix}} \end{array}\tag{2.17}
這兩個純量積恰好是之前所說的 差向量 與 各自平移向量 的純量積(作為練習,請大家自行在圖中指出上述兩個向量)。有了這兩個純量積之後現在我們整合一下之前的說法。對於 x 方向上的計算:
- f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)>0 蘊涵了純量積 (2.16) 為正,此時水平方向上的高度 y_0 處的流出量為正;
- f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)<0 蘊涵了純量積 (2.16) 為負,此時水平方向上的高度 y_0 處的流出量為負;
- f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)=0 蘊涵了純量積 (2.16) 為零,此時水平方向上的高度 y_0 處的流出量為零;
對於 y 方向上的計算:
- f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)>0 蘊涵了純量積 (2.17) 為正,此時豎直方向上水平為 x_0 處的流出量為正;
- f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)<0 蘊涵了純量積 (2.17) 為負,此時豎直方向上水平為 x_0 處的流出量為負;
- f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)=0 蘊涵了純量積 (2.17) 為零,此時豎直方向上水平為 x_0 處的流出量為零;
別著急出鍋哦,還差一味佐料。這味佐料謂之——求和。我們將沒處理前的式 (2.4) 與式 (2.10) 求和可得:
\begin{array}{ll} & \display style{\frac{f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)}{\Delta x}\cdot\Delta x\cdot\Delta y +\frac{f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)}{\Delta y}\cdot\Delta x\cdot\Delta y} \\ =& \display style{\left(\frac{f_{x}(x_0+\Delta x,y_0)-f_{x}(x_0,y_0)}{\Delta x}+\frac{f_{y}(x_0,y_0+\Delta y)-f_{y}(x_0,y_0)}{\Delta y}\right)\cdot\Delta A} \end{array} .\tag{2.18}
現在我們不固定點了,也就是把式 (2.18) 中的點 (x_0,y_0) 換成 (x,y) ,換完之後就變成了:
\Psi:=\left(\frac{f_{x}(x+\Delta x,y)-f_{x}(x,y)}{\Delta x}+\frac{f_{y}(x,y+\Delta y)-f_{y}(x,y)}{\Delta y}\right)\cdot\Delta A\tag{2.19}.
此時我們也不需要在固定點描述流出量了。因此式 (2.19) 表示的就是向量場 \vec{f}(x,y) 在圖片 12 (或圖片 13 )中的矩形的總流出量。顯然,總流出量的值也分為三種情況:
- 總流出量 \Psi>0 。此時向量場 \vec{f}(x,y) 在圖片 12 (或圖片 13 )中的矩形中具有 發散傾向 ;
- 總流出量 \Psi<0 。此時向量場 \vec{f}(x,y) 在圖片 12 (或圖片 13 )中的矩形中具有 匯聚傾向 ;
- 總流出量 \Psi=0 。此時向量場 \vec{f}(x,y) 在圖片 12 (或圖片 13 )中的矩形中既不具有匯聚傾向,也不具有發散傾向。
進而單位面積的總流出量為:
\frac{\Psi}{\Delta A}:=\overline{\Psi}_{\Delta A}=\frac{f_{x}(x+\Delta x,y)-f_{x}(x,y)}{\Delta x}+\frac{f_{y}(x,y+\Delta y)-f_{y}(x,y)}{\Delta y}\tag{2.20}.
截止到目前,還都是一些「宏觀的」計算和討論。現在我們考慮向量場 \vec{f}(x,y) 在點 (x,y) 「附近」的發散和匯聚程度。
為此我們可以對式 (2.20) 的兩側取 \Delta x,\,\Delta y\to0 的極限值:
\begin{array}{ll} \display style{\lim_{\Delta x,\,\Delta y\to0}\frac{\Psi}{\Delta A}} & \display style{=\lim_{\Delta x\to0,\,\Delta y=0}\frac{f_{x}(x+\Delta x,y)-f_{x}(x,y)}{\Delta x}+\lim_{\Delta x=0,\,\Delta y\to0}\frac{f_{y}(x,y+\Delta y)-f_{y}(x,y)}{\Delta y}} \\ & \display style{=\frac{\partial}{\partial x}f_{x}(x,y)+\frac{\partial}{\partial y}f_{y}(x,y)}.\tag{2.21} \end{array}
在式 (2.21) 中由偏導數的定義有:
\lim_{\Delta x\to0,\,\Delta y=0}\frac{f_{x}(x+\Delta x,y)-f_{x}(x,y)}{\Delta x}=\frac{\partial}{\partial x}f_{x}(x,y),\quad \lim_{\Delta x=0,\,\Delta y\to0}\frac{f_{y}(x+\Delta x,y)-f_{y}(x,y)}{\Delta y}=\frac{\partial}{\partial y}f_{y}(x,y).\tag{2.22}
最終有:
\boxed{\lim_{\Delta x,\,\Delta y\to0}\frac{\Psi}{\Delta A}=\lim_{\Delta A\to 0}\overline{\Psi}_{\Delta A}=\frac{\partial}{\partial x}f_{x}(x,y)+\frac{\partial}{\partial y}f_{y}(x,y)}.\tag{2.23}
也就是說:
- \lim_{\Delta A\to 0}\overline{\Psi}_{\Delta A}>0 ,此時向量場 \vec{f}(x,y) 點 (x,y) 「附近」具有 發散傾向 。並且,該值越大,向量場 \vec{f}(x,y) 點 (x,y) 「附近」的發散程度越大;
- \lim_{\Delta A\to 0}\overline{\Psi}_{\Delta A}<0 ,此時向量場 \vec{f}(x,y) 點 (x,y) 「附近」具有 匯聚傾向 。並且,該值越小,向量場 \vec{f}(x,y) 點 (x,y) 「附近」的匯聚程度越大;
- \lim_{\Delta A\to 0}\overline{\Psi}_{\Delta A}=0 ,此時向量場 \vec{f}(x,y) 點 (x,y) 「附近」既不具有匯聚傾向,也不具有發散傾向。
為了描述這種 發散或者匯聚的程度 ,我們引入一個新的名詞,相信我不說大家也知道它是什麽了,沒錯,都說到現在了,只能是 散度(divergence) 了。
第一波計算算是告一段落了,是時候做一次全面的整合了。

剛才我們匯出的式 (2.23) 是平面向量場的散度。但是式 (2.23) 左側的記號不是很好看,我們現在給它換一個好看的算符:
\lim_{\Delta x,\,\Delta y\to0}\frac{\Psi}{\Delta A}=\lim_{\Delta A\to 0}\overline{\Psi}_{\Delta A}=\frac{\partial}{\partial x}f_{x}(x,y)+\frac{\partial}{\partial y}f_{y}(x,y):=\vec{\bigtriangledown}\cdot\vec{f}\tag{2.24}
這個倒三角算子稱為 Nabla—算子 ,它的名字來自希臘語中一種被稱為納布拉琴的豎琴。平面上的 Nabla 算子的具體形式是:
\vec{\bigtriangledown}=\begin{pmatrix} \dfrac{\partial}{\partial x}\\ \dfrac{\partial}{\partial y} \end{pmatrix}.\tag{2.25}
它是一個向量微分算子。並且,我們在式 (2.24) 中看到了純量積。我們將散度記作 Nabla 算子與向量場 \vec{f} 的純量積形式並非電洞來風,回溯一下,之前反復提到的差向量與平移向量的純量積的正負可以反映出平移方向上的流出量的正負,將這些不同方向上的流出量求和可以反映出向量場在「某一塊區域」上總的流出量的正負,進而反映出向量場在該「區域」上的發散或匯聚傾向,而當所考察的區域充分小的時候反映的則是在考察點「附近」的向量場的發散或匯聚傾向,因此我們可以說:
差向量與平移向量的純量積在散度為正時 傾向 為正,反之亦然。
註意,上面我用了「傾向」一詞,而不是「一定」。這裏我可能又得廢話一句了。
為啥是傾向而不是一定呢?因為 總流出量為正並不能說明某一方向上的流出量不能為負呀 。
我廢話完了。

不過只停留在平面上多沒意思,高一個維度試試?走著。
高一個維度之後向量場也會長高一節:
\vec{f}\left(x,y,z\right):=\begin{pmatrix} f_{x}(x,y,z)\\ f_{y}(x,y,z)\\ f_{z}(x,y,z) \end{pmatrix}\tag{2.26}.
沒錯,他還胖了一圈。長大之後的向量場 \vec{f} 已經不滿足於穿過平面上的線段了,它要穿過空間上的平面!

不對,拿錯武器了:
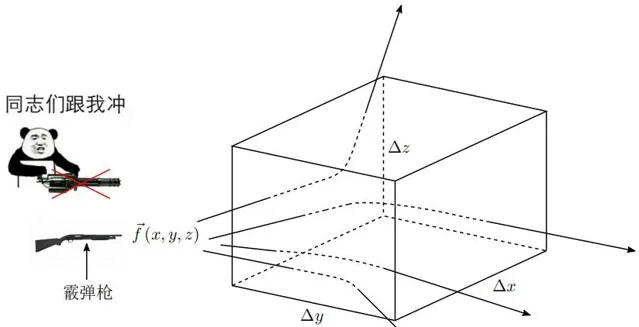
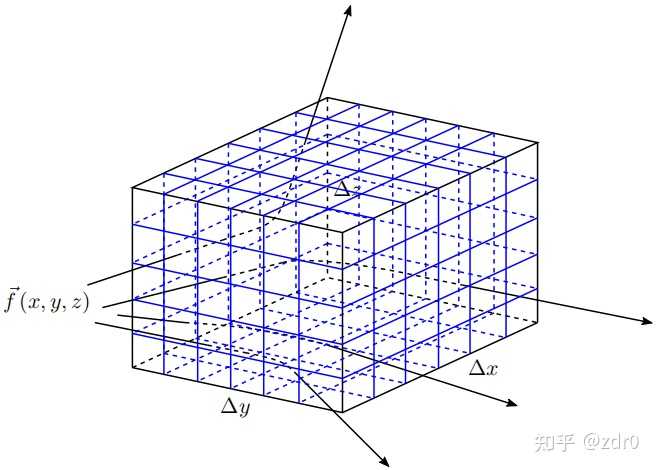
類比之前對平面向量場的分析可知,向量場 \vec{f}(x,y,z) 在圖片 14 中的長方體中的總流出量為:
\begin{array}{ll} \display style{\Psi} & \display style{:=\left({f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}\right)\cdot{\Delta y}\cdot\Delta z}\\ & \display style{+\left({f_{y}(x,y+\Delta y,z)-f_{y}(x,y,z)}\right)\cdot{\Delta x}\cdot\Delta z}\\ & \display style{+\left({f_{z}(x,y,z+\Delta z)-f_{z}(x,y,z)}\right)\cdot{\Delta x}\cdot\Delta y} \end{array}\tag{2.27}.
如果記該長方體的體積為 \Delta V=:\Delta x\cdot \Delta y\cdot \Delta z ,我們可以將式 (2.27) 寫為:
\Psi:=\left(\frac{f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}{\Delta x}+\frac{f_{y}(x,y+\Delta y,z)-f_{y}(x,y,z)}{\Delta y}+\frac{f_{z}(x,y,z+\Delta z)-f_{z}(x,y,z)}{\Delta z}\right)\cdot\Delta V\tag{2.28}.
進而單位體積的總流出量為:
\frac{\Psi}{\Delta V}:=\overline{\Psi}_{\Delta V}:=\frac{f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}{\Delta x}+\frac{f_{y}(x,y+\Delta y,z)-f_{y}(x,y,z)}{\Delta y}+\frac{f_{z}(x,y,z+\Delta z)-f_{z}(x,y,z)}{\Delta z}.\tag{2.29}
現在對式 (2.29) 我們同樣取 \Delta V\to 0 時的極限可得:
\begin{array}{ll} \display style{\lim_{\Delta V\to 0}\frac{\Psi}{\Delta V}} & \display style{=\lim_{\Delta x\to 0,\,\Delta y,\,\Delta z=0}\frac{f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}{\Delta x}} \\ & \display style{+\lim_{\Delta y\to 0,\,\Delta x,\,\Delta z=0}\frac{f_{y}(x,y+\Delta y,z)-f_{y}(x,y,z)}{\Delta y}} \\ & \display style{+\lim_{\Delta z\to 0,\,\Delta x,\,\Delta y=0}\frac{f_{z}(x,y,z+\Delta z)-f_{z}(x,y,z)}{\Delta z}} \end{array}.\tag{2.30}
則由偏導數的定義:
\begin{array}{ll} \display style{\frac{\partial}{\partial x}f_x(x,y,z)} & \display style{=\lim_{\Delta x\to 0,\,\Delta y,\,\Delta z=0}\frac{f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}{\Delta x}} \\ \display style{\frac{\partial}{\partial y}f_y(x,y,z)} & \display style{=\lim_{\Delta y\to 0,\,\Delta x,\,\Delta z=0}\frac{f_{y}(x,y+\Delta y,z)-f_{y}(x,y,z)}{\Delta y}} \\ \display style{\frac{\partial}{\partial z}f_z(x,y,z)} & \display style{=\lim_{\Delta z\to 0,\,\Delta x,\,\Delta y=0}\frac{f_{z}(x,y,z+\Delta z)-f_{z}(x,y,z)}{\Delta z}} \end{array}\tag{2.31}
也就是說:
\boxed{\lim_{\Delta V\to 0}\frac{\Psi}{\Delta V}=\frac{\partial}{\partial x}f_x(x,y,z)+\frac{\partial}{\partial y}f_y(x,y,z)+\frac{\partial}{\partial z}f_z(x,y,z).}\tag{2.32}
與平面向量場一樣,取 \Delta V\to 0 時的極限得到的是向量場 \vec{f}(x,y,z) 在考察點「附近」的發散或者匯聚的程度。而且非常棒的一點是,之前所述的差向量與平移向量的純量積的觀點此處也是適用的,大家不妨自己思考一下。
定義空間中的 Nabla-算符之後:
\vec{\bigtriangledown}=\begin{pmatrix} \dfrac{\partial}{\partial x}\\ \dfrac{\partial}{\partial y}\\\dfrac{\partial}{\partial z} \end{pmatrix}\tag{2.33}
我們可以將向量場 \vec{f}(x,y,z) 的散度寫為:
\vec{\bigtriangledown}\cdot\vec{f}(x,y,z)=\frac{\partial}{\partial x}f_x(x,y,z)+\frac{\partial}{\partial y}f_y(x,y,z)+\frac{\partial}{\partial z}f_z(x,y,z).\tag{2.34}
散度算是介紹完了。不過你以為要閉幕啦?還早呢,壓軸好戲即將上演。
終於來到了 Gauß 散度定理
咋辦咋辦咋辦,我該怎麽解釋散度定理?
我們需要一味原材料,它是我們剛才多次提到的流出量 \Psi ,不過這裏我們要給它改個名字 — 通量 , 並且為了正式一點,我們也給它換個記號 \Phi 。通量這個名字還是很形象的,顧名思義,通量就是指透過的量嘛,在之前的分析中我們也發現,在計算一個向量場透過一個平面的通量時,我們所取的是向量場中與該平面正交的分量,因為只有這一部份才是向量場真正透過這個平面的量。現在我們就要想了:該如何計算向量場透過一個面(這個面可以是(封閉的)平面,也可以是(封閉的)曲面)的通量呢?

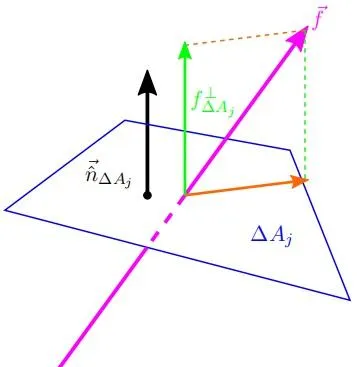
先給圖片 15 打碎,再取一面積 \Delta A_j 。現在假設,假設啊,有一個向量場 \vec{f} 從 \Delta A_j 的後面穿出來,我們將這個向量場垂直於 \Delta A_j 的分量記作 f_{\Delta A_j}^{\bot} ,那麽顯然,向量場 \vec{f} 透過面積 \Delta A_j 的通量為:
\Phi_{\Delta A_j}=f_{\Delta A_j}^{\bot}\cdot\Delta A_j.\tag{2.35}
但是現在有一個問題,就是 f_{\Delta A_j}^{\bot} 這種表達方式實在是不簡潔。我們不就是要表達向量場 \vec{f} 垂直於 \Delta A_j 的分量嗎?那麽純量積就是一個趁手的工具呀。也就是說,我們可以將向量場 \vec{f} 向 \Delta A_j 的法向投影。這樣的話就需要給 \Delta A_j 一個方向了,我們可以將 \Delta A_j 記作向量形式:
\Delta \vec{A}_j:=\vec{\hat{n}}_{\Delta{A}_j}\cdot \Delta{A}_j\tag{2.36}.
其中 \vec{\hat{n}}_{\Delta{A}_j} 表示的是 \Delta A_j 的 單位法向量 ,它給出了 \Delta A_j 的方向。由此,當我們將向量場 \vec{f} 向 \Delta A_j 的法向投影時,成立:
f_{\Delta A_j}^{\bot}=\vec{f}\cdot\vec{\hat{n}}_{\Delta{A}_j}.\tag{2.37}
進而向量場 \vec{f} 透過面積 \Delta A_j 的通量為:
\Phi_{\Delta A_j}=f_{\Delta A_j}^{\bot}\cdot\Delta A_j=\vec{f}\cdot\vec{\hat{n}}_{\Delta{A}_j}\cdot\Delta A_j=\vec{f}\cdot\Delta \vec{A}_j.\tag{2.38}
那麽向量場 \vec{f} 穿過「還真有你的」的總通量該如何計算呢?對 j (即對所有碎片)求和就完事兒了:
\Phi_A^*=\sum_j\Phi_{\Delta A_j}=\sum_j\vec{f}\cdot\Delta \vec{A}_j.\tag{2.39}
如果我們把圖片 15 再整稀碎一點呢?

那麽之前的 \Delta A_j 不復存在了,取而代之的是更小的 \Delta A_j ,你看,字都變小了是不是?那麽當 \Delta A_j 變得再小一點,再小一點,再小一點意味著什麽呢?是不是就意味著「還真有你的」碎成了無窮多個渣渣,也就是說有無窮多個無限小的 \Delta A_j (即 \Delta A_j\to 0 )。那麽此時穿過「還真有你的」的總通量就是:
\Phi_A:=\lim_{j\to+\infty}\Phi_A^*=\lim_{j\to+\infty}\sum_j\Phi_{\Delta A_j}=\lim_{j\to+\infty}\sum_j\vec{f}\cdot\Delta \vec{A}_j.\tag{2.40}
換個記號:
\boxed{\Phi_A=\lim_{j\to+\infty}\sum_j\vec{f}\cdot\Delta \vec{A}_j=\int_{A}\vec{f}\cdot\mathrm{d}\vec{A}.}\tag{2.41}
有些情況下我們也將 \int_{A}\vec{f}\cdot\mathrm{d}\vec{A} 中的點乘省掉,直接記作 \int_{A}\vec{f}\,\mathrm{d}\vec{A} 。其中 \int_{A}\vec{f}\,\mathrm{d}\vec{A} 稱為 向量場 \vec{f} 的曲面積分 ,或者稱為 第二類曲面積分 。也就是說: 向量場 \vec{f} 穿過任意一個平面(或者曲面) A 的通量 \Phi_{A} 都可以透過向量場 \vec{f} 對 A 的曲面積分進行計算 。特別的,當曲面 A 是一個封閉曲面時,我們給積分號帶一箍,記作:
\oint_{A}\vec{f}\,\mathrm{d}\vec{A}\tag{2.42}
這個箍沒啥特殊的,只是為了區分對封閉曲面和非封閉曲面的曲面積分。
現在我們有了通量的一般算式了,即式 (2.41) 。現在我們將式 (2.34) 與式 (2.41) 一起代回到式 (2.32) 中會得到一個略顯復雜的式子:
{\lim_{\Delta V\to 0}\frac{\display style{\int_{A}\vec{f}\,\mathrm{d}\vec{A}}}{\Delta V}=\vec{\bigtriangledown}\cdot\vec{f}.}\tag{2.43 ?}
哎,這裏好像有點問題啊。如果曲面 A 不是封閉的,那麽這裏的體積 \Delta V 與曲面 A 有什麽關系呢?
- 如果兩者沒有一點關系,那我們就不做討論了。
-
如果此時的非封閉曲面 A
為體積 \Delta V
的某一個邊界面,比如之前討論時使用的長方體的某一個面,則由之前的討論我們知道此時 \int_{A}\vec{f}\,\mathrm{d}\vec{A}
表示的是這一個面的通量,但是,這一個面的通量只對應了這一個面的「散度」。為啥呢?自己想吧哈哈哈哈哈。給個提示:考察 A:=\Delta y\cdot \Delta z
,以及 \Delta V=\Delta x\cdot\Delta y\cdot\Delta z
還有:
\Phi_x=\left({f_{x}(x+\Delta x,y,z)-f_{x}(x,y,z)}\right)\cdot{\Delta y}\cdot\Delta z\tag{2.44}.
在結合第一節末尾的講解即可獲得答案。
也就是說,如果 \Delta V 與曲面 A 沒有什麽特殊的關系的話式 (2.43) 是不成立的呀。還是之前長方體通量的例子,如果要將通量與散度透過式 (2.43) 那種形式聯系起來,那麽我們只需要讓曲面 A 是 \Delta V 的「全部邊界」就可以了。在長方體通量的例子中,「全部邊界」指的就是長方體的六個面。此時我們將曲面 A 記作 \partial \Delta V ,表示它是 \Delta V 的「全部邊界」。顯然,這種情況下的曲面 A 是封閉的。因此,真正的式 (2.43) 應該為:
\lim_{\Delta V\to 0}\frac{\display style{\oint_{A=\partial\Delta V}\vec{f}\,\mathrm{d}\vec{A}}}{\Delta V}=\vec{\bigtriangledown}\cdot\vec{f}.\tag{real 2.43:=2.45}
式 (2.45) 其實已經隱藏了 Gauß 散度定理了,下面我就以一種啟發性的方式來解釋 Gauß 散度定理。在開始解釋之前,首先約定:
閉合曲面的單位法向量總是指向外側的。
首先讓我來擺個陣法。
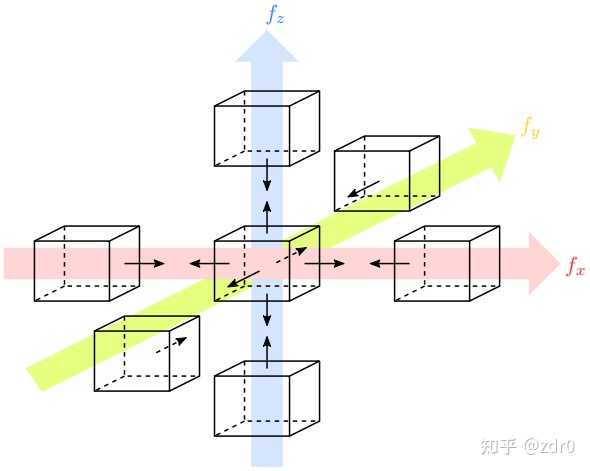
下面讓我來簡單介紹一下這個陣法。此陣法總共采用了七個相同的長方體進行布陣,位於陣法中心的長方體被標註了六個方向的單位法向量。如六個黑色箭頭所示。它周圍的六大護法分別位於其正前、正後、正上、正下、正左以及正右。並且在各個方向上標註了與中心長方體方向相反的單位法向量。且 f_{x,y,z} 分別表示向量場 \vec{f}(x,y,z) 在三個方向上的分量。
現在我們做一件事情:我們只看 x 方向。我們把中心長方體還有它的左右護法拼在一起,這樣做會發生一個奇妙的現象,就是拼接面的單位法向量是反向的。
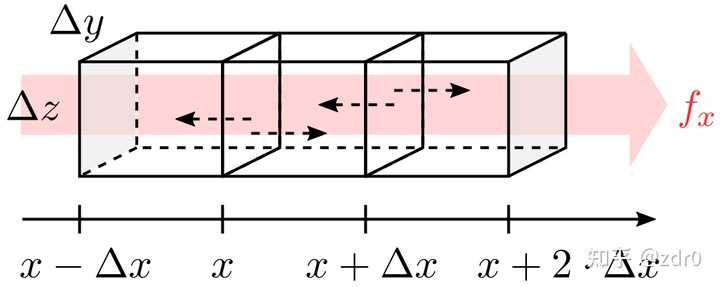
這說明了啥呢?這可太爽了,比如對於左邊的拼接面來講,向量場 \vec{f}(x,y,z) 的總通量為:
\Phi_{x,L}=f_x(x,y,z)\cdot \Delta y\cdot \Delta z-f_x(x,y,z)\cdot \Delta y\cdot \Delta z=0.\tag{2.46}
而對於右邊的拼接面來講,向量場 \vec{f}(x,y,z) 的總通量為:
\Phi_{x,R}=f_x(x+\Delta x,y,z)\cdot \Delta y\cdot \Delta z-f_x(x+\Delta x,y,z)\cdot \Delta y\cdot \Delta z=0.\tag{2.47}
嗯?!拼接面處的通量都消失啦!所以向量場 \vec{f}(x,y,z) 在水平方向的總通量為最左端與最右端面的通量之和,即:
\Phi_{x}=f_x(x-\Delta x,y,z)\cdot \Delta y\cdot \Delta z-f_x(x+2\cdot \Delta x,y,z)\cdot \Delta y\cdot \Delta z.\tag{2.48}
其他兩個方向同理,就不再看啦。
經過這麽一整我們最終可以發現,中心長方體的通量沒有了!
當我們將圖片 14 中的長方體進行切割時,會出現很多個拼接面。
這些拼接面的單位法向量方向都是相反的。 因此,向量場 \vec{f}(x,y,z) 對這些拼接面的通量都為零。於是,向量場 \vec{f}(x,y,z) 對體積 \Delta x\cdot \Delta y\cdot \Delta z 的通量僅由體積 \Delta x\cdot \Delta y\cdot \Delta z 的邊界,即長方體的六個面決定 。
我之所以要講這個問題,是因為我們馬上可以直接「推導」 Gauß 散度定理。
在圖片 18 中,我們將其中一個分割好的小體積記作 \Delta V_j:=\Delta x_j\cdot \Delta y_j\cdot \Delta z_j ,它的邊界記作 \partial\Delta V_j 。現在讓我們回到式 (2.28) 。並將通量 \Psi=\Phi 寫為第二類曲面積分的形式:
\oint_{A=\part\Delta V_j}\vec{f}\,\mathrm{d}\vec{A}=\left(\frac{f_{x}(x+\Delta x_j,y,z)-f_{x}(x,y,z)}{\Delta x_j}+\frac{f_{y}(x,y+\Delta y_j,z)-f_{y}(x,y,z)}{\Delta y_j}+\frac{f_{z}(x,y,z+\Delta z_j)-f_{z}(x,y,z)}{\Delta z_j}\right)\cdot\Delta V_j\tag{2.49}
然後我們對圖片 18 中的所有的小體積求和,即對 j 求和可得:
\sum_j\oint_{A=\part\Delta V_j}\vec{f}\,\mathrm{d}\vec{A}=\sum_j\left(\frac{f_{x}(x+\Delta x_j,y,z)-f_{x}(x,y,z)}{\Delta x_j}+\frac{f_{y}(x,y+\Delta y_j,z)-f_{y}(x,y,z)}{\Delta y_j}+\frac{f_{z}(x,y,z+\Delta z_j)-f_{z}(x,y,z)}{\Delta z_j}\right)\cdot\Delta V_j\tag{2.50}
當我們將圖片 14 中的長方體分割成為無限多個小體積時,成立 j\to+\infty ,並且此時每個小體積的體積 \Delta V_j 也是趨於零的,因此當我們對式 (2.50) 的右側求極限,並參考式 (2.30) 與式 (2.31) 時成立:
\begin{array}{ll} &\display style{\lim_{j\to +\infty}\sum_j\left(\frac{f_{x}(x+\Delta x_j,y,z)-f_{x}(x,y,z)}{\Delta x_j}+\frac{f_{y}(x,y+\Delta y_j,z)-f_{y}(x,y,z)}{\Delta y_j}+\frac{f_{z}(x,y,z+\Delta z_j)-f_{z}(x,y,z)}{\Delta z_j}\right)\cdot\Delta V_j}\\ =&\display style{\lim_{\Delta V_j\to 0}\sum_j\left(\frac{f_{x}(x+\Delta x_j,y,z)-f_{x}(x,y,z)}{\Delta x_j}+\frac{f_{y}(x,y+\Delta y_j,z)-f_{y}(x,y,z)}{\Delta y_j}+\frac{f_{z}(x,y,z+\Delta z_j)-f_{z}(x,y,z)}{\Delta z_j}\right)\cdot\Delta V_j}\\ = & \display style{\sum_j\lim_{\Delta V_j\to 0}\left(\frac{f_{x}(x+\Delta x_j,y,z)-f_{x}(x,y,z)}{\Delta x_j}+\frac{f_{y}(x,y+\Delta y_j,z)-f_{y}(x,y,z)}{\Delta y_j}+\frac{f_{z}(x,y,z+\Delta z_j)-f_{z}(x,y,z)}{\Delta z_j}\right)\cdot\Delta V_j} \\ =& \display style{\int_{V}\left(\frac{\partial}{\partial x}f_x(x,y,z)+\frac{\partial}{\partial y}f_y(x,y,z)+\frac{\partial}{\partial z}f_z(x,y,z)\right)\,\mathrm{d}V}\\ =& \display style{\int_{V}\vec{\bigtriangledown}\cdot \vec{f}\,\mathrm{d}V} \end{array}.\tag{2.51}
而當我們對式 (2.50) 取 j\to+\infty 的極限時成立:
\lim_{j\to+\infty}\sum_j\oint_{A_j=\partial\Delta V_j}\vec{f}\,\mathrm{d}\vec{A}_j=\lim_{j\to+\infty}\left(\oint_{A_1=\part\Delta V_1}\vec{f}\,\mathrm{d}\vec{A}_1+\oint_{A_1=\part\Delta V_2}\vec{f}\,\mathrm{d}\vec{A}_2+\ldots\right)=\oint_{\partial V}\vec{f}\,\mathrm{d}\vec{A}.\tag{2.52}
在式 (2.51) 與式 (2.52) 中, V 表示圖片 14 中的長方體的體積,而 \partial V 表示的則是它的邊界(即長方體的六個面)。在式 (2.52) 中,雖然我們將圖片 14 中的長方體分割成了無限多個,但是這依然不妨礙向量場 \vec{f}(x,y,z) 對這些分割後的小體積的拼接面的通量為零。也就是說,無論我們將圖片 14 中的長方體分割地多麽細致,向量場 \vec{f}(x,y,z) 對它的通量也僅由其邊界面決定。這就是式 (2.52) 成立的原因。
綜上所述,聯立式 (2.51) 和式 (2.52) 後最終成立:
\boxed{\int_{V}\vec{\bigtriangledown}\cdot \vec{f}\,\mathrm{d}V=\int_{\partial V}\vec{f}\,\mathrm{d}\vec{A}.}\tag{2.53}
式 (2.53) 就是著名的 Gauß 散度定理了。
參考
- ^https://www.bilibili.com/video/BV19s41157Z4?from=search&seid=16795908421145065898&spm_id_from=333.337.0.0
- ^ 平面向量場繪制 https://academo.org/demos/vector-field-plotter/











