如果每2∧n秒(n=1,2,3,4,…)獲得100,000元代替一生的薪資，我賺了嗎？

2022-07-08財經

細一看，這不就是一個很經典的金融題目嘛~

已知現金流，折現率，計算NPV，然後看選擇投哪個計畫嘛。這題我會。

而且既然被邀請了，那就算一下吧。

前提假設

假設在兩種情況下，

張三(題主)的消費情況類似。
張三不會因為生活的富足程度改變生活習慣或者壽命，並且同樣都可以活到80歲
不考慮稅收問題，都為稅後收入。

折現率=通脹率=理財預期報酬=5%

NPV: Net Present Value 凈現值
凈現值指未來資金（現金）流入（收入）現值與未來資金（現金）流出（支出）現值的差額，是計畫評估中凈現值法的基本指標。未來的資金流入與資金流出均按預計折現率各個時期的現值系數換算為現值後，再確定其凈現值。這種預計折現率是按企業的最低的投資收益率來確定的.是企業投資可以接受的最低界限。 ^[1]
NPV=∑(CI-CO)(1+i)^(-t)
CI: 收益； CO: 支出； i 折現率； t 時間
上面這段來源於百度。
簡單地NPV就是將未來的凈收入/凈支出貼現到T0(現在)的值。

第一種情況

在第一種情況先算出總共能夠獲得的次數

大概是1歲的時候獲得25次的收益，然後在68歲的時候獲得最後一筆收入。

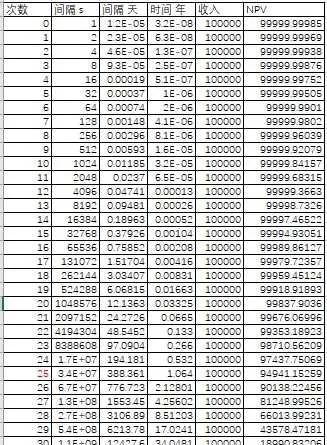
總凈現值 NPV_{1} 為2，893，371

總收入(不考慮時間成本)為3，200，000

以下是計算方法:
1. 間隔s 代表的是在第幾秒的時候可以收到第n次收益=2^n
如張三獲得第10次收益的時間為2^10=1024秒
2. 間隔天就是簡單地把秒換算成天=間隔s/60/60/24
3. 間隔年就是再把天數換算成年，= 間隔天/365 (這裏沒有考慮閏年的情況，因為不會過多地影響最終答案。)
如在張三想獲得第32次收益時，他需要活的年數 = 2^32/60/60/24/365=136.19 (年)
很明顯的大於目前的人類平均壽命，故排除。
4. NPV= 收入*(1+5%)^(-t)

第二種情況

薪資假設1

假設張三於22歲大學畢業，開始工作。初始薪資為8000元每月。

由於他勤勤懇懇地工作，老板大為感動，每年加薪2220元。

並且由於張三是男性，在60周歲時成功退休。

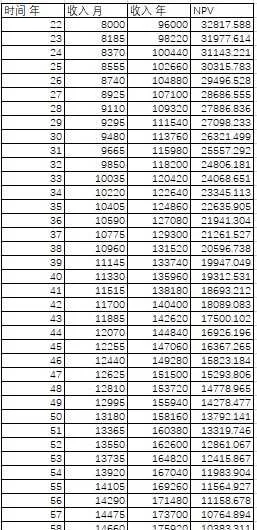
總凈現值NPV_{2.1} 為764，880

總收入(不考慮時間成本)為5，389，020

以下是計算方法:
收入年=收入月*12
NPV的計算方式同情況1
e.g. 在22歲時的96000元的凈現值= 96000*(1+5%)^(-22)=32818

薪資假設2

假設張三於22歲大學畢業，開始工作。初始薪資為8000元每月。

由於他勤勤懇懇地工作，並且老板不差錢，公司增長業績喜人，每年升薪5%。

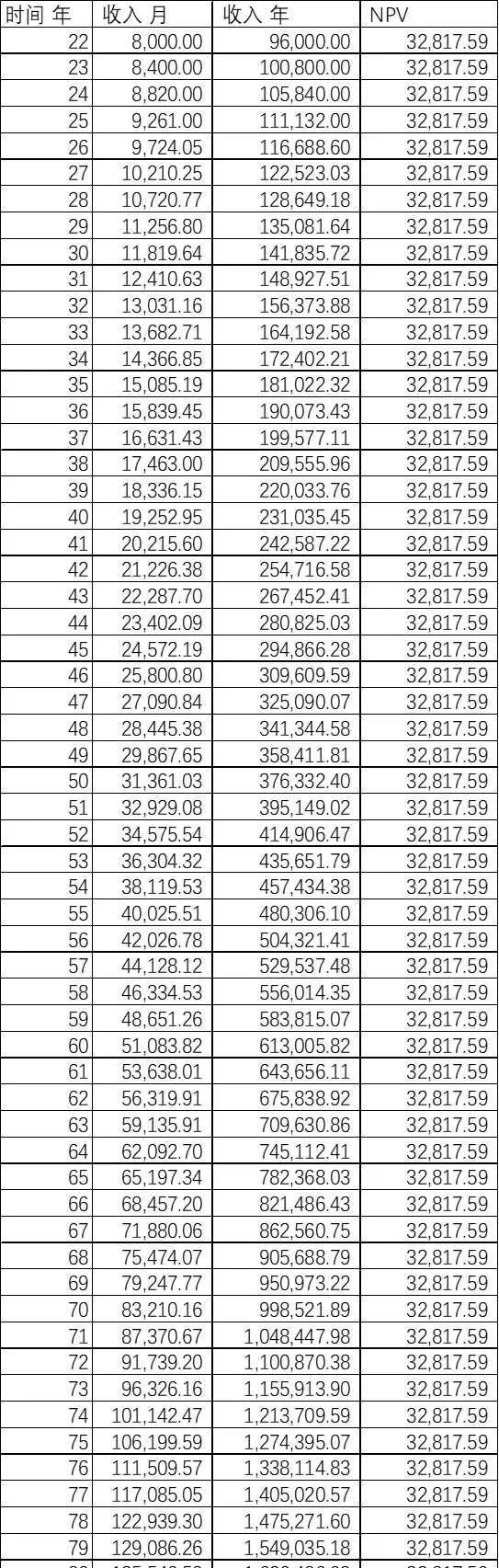
總凈現值NPV_{2.2} 為1，936,237.67

總收入(不考慮時間成本)為32,236,225.63

計算方式同薪資假設1
收入=上一年薪資*(1+5%)

薪資假設3

假設張三於22歲在世界名牌大學畢業並於畢業後立即開始工作。初始薪資為8000元每月。

由於他天資聰穎，技術一流，踏實肯幹，持續精進；並且非常幸運地加入到了一家後來成為與鵝廠媲美的獨角獸公司；成功公司技術骨幹；老板青睞有加；公司業績持續穩定大幅增長；每年升薪同天朝2009-2019年的平均GDP增幅7.84%。(近兩年因為疫情，GDP波動較大，故不引入)

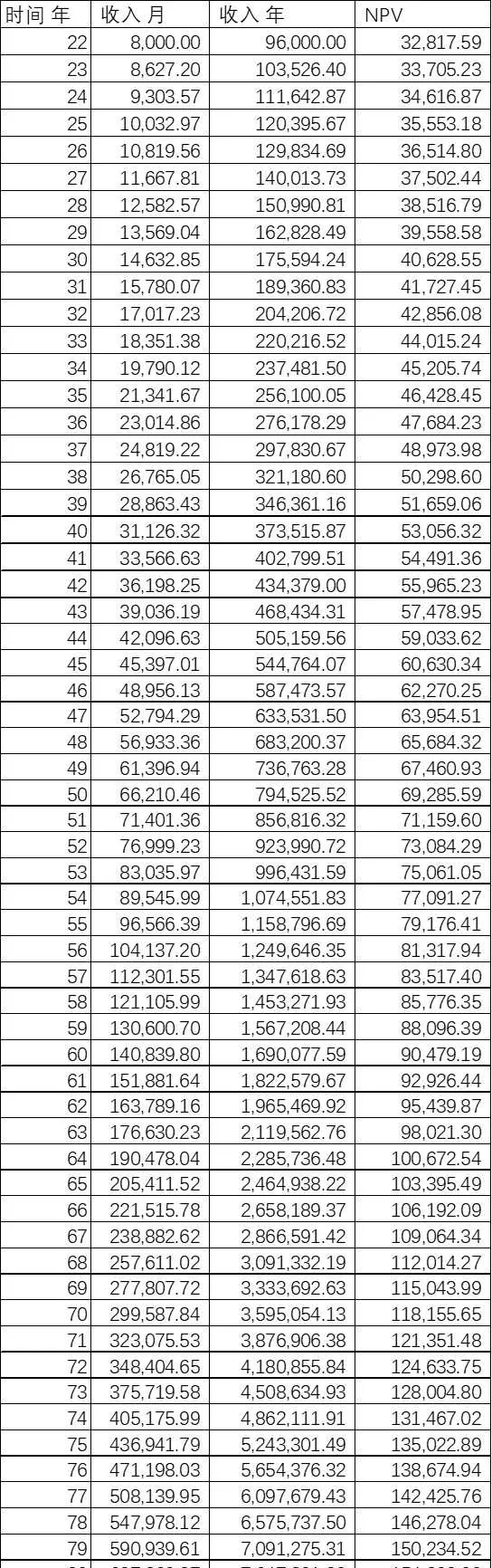
總凈現值NPV_{2.3} 為4，645,651.32

總收入(不考慮時間成本)為103,963,957.06

計算方式同薪資假設1
收入=上一年薪資*(1+7.84%)

結論

(NPV_{2.3} =4，645,651.32)>(NPV_{1} =2，893，371 ) >(NPV_{2.2} =1，936,237.67)>( NPV_{2.1} =764，880)

若覺得自己的能力夠強，選第二種。

其他情況下，請保守選擇第一種。

一些補充說明

一、貨幣的時間價值

在這裏，細心的朋友應該發現了，張三在第二種情況下其實獲得的總收入5，389，020是大於在第一種情況下的總收入3，200，000。但是為什麽我還是推薦選擇第一種呢？

為什麽今天的100元比1年後的100元更加值錢？
1、現時消費，就是早用早享受。
在通脹時期，大多數人都更加傾向於更早地享受這筆錢。
今天買入一只包包，肯定比明年再買這只包包來的爽呀。對小朋友來說，現在吃到1顆糖的快感肯定比1天後吃到同樣1顆糖來的高。(即使在通脹=0的情況下也是成立的)
2、貨幣的潛在收益。也就是機會成本。
錢是可以生錢的。當你存在了銀行，又或者是買了理財，這100元在一年後的利息+本金是會大於100元的。又或者你拿這100元在曾經的西子湖畔將這100元投資給了一個姓馬的年輕人。
這些可能獲得的收益，就是貨幣的機會成本。
3、通脹導致的貨幣貶值。這也就是為什麽我們存錢到銀行，銀行要給你利息。以及為什麽我們向銀行貸款，我們要付利息給銀行。

接著，讓我們回到假設。

0歲的張三，將他獲得的第一筆10萬元存入買入理財。(因為假設中所說通脹率:5%，理財收益率也為5%，那麽可以認為這個理財就是無風險的了。)

那麽這10萬元在他22歲時，就可以獲得

10*(1+5%)^22=29.25萬

這也就是巴菲特所說的復利的奇跡。

二、NPV

詳見第一部份

三、第二種情況的薪資增長假設問題。

其實，我最先的假設是每年薪資上漲5%，一算後發現到60歲時已經上漲到了61萬每年。一想，就算我同意這漲法，張三老板應該不會同意的。

於是就改用了更加符合現實的線性薪資增長。薪資上限就偷了個懶，直接取了個題目中已知的，中級程式設計師的巔峰。

如果大家想要更精確地計算的話，可以在這裏回復下你們最近5年的薪資每年各漲了多少及上漲百分比，有升職的話要標註下哦。我做個比較合乎現實的版本。

不過結論理論上不會差距太大的。畢竟按百分比漲薪資的機率太小。