 https://www.zhihu.com/video/1577308476673560576
https://www.zhihu.com/video/1577308476673560576

作者:自動駕駛人 | 原文出處: 公眾號【自動駕駛專欄】
摘要
本文提出了一種使用6自由度運動的兩軸雷射雷達的距離測量結果來實作即時裏程計和建圖的方法。這個問題很困難,因為雷射雷達的距離測量結果是在不同時刻收到的,並且運動估計的誤差將導致目標點雲誤匹配。至今為止,離線的批次方法能夠建立清晰的3D地圖,通常使用閉環檢測來校正隨時間的漂移。本文提出的方法能夠在不需要高精度測距或者慣性測量單元的情況下,實作低漂移和低計算復雜度的定位和建圖。為了取得這樣的效能,本文的核心思想是將同時定位和建圖這個同時最佳化大量變量的復雜問題分離為兩種演算法。一種演算法是實作高頻率但低精度的裏程計來估計雷射雷達速度,另一種演算法則實作低頻率但高精度的點雲匹配與配準。這兩種演算法的組合使得建圖方法可以即時執行。該方法已經被大量實驗和 KITTI 裏程計數據集所評估和驗證。結果表明,該方法能夠與目前(論文創作時)最先進的離線批次方法達到同級別的精度。
介紹
3D建圖是一種常用的技術。使用雷射雷達建圖很常見,因為雷射雷達能夠提供高頻率的距離測量,且該測量誤差相對固定,不受測量距離的影響。如果雷射雷達唯一的運動只是旋轉一條雷射束時,點雲配準就較為簡單。然而,如果雷射雷達在很多有趣的套用中需要運動那樣,精確的建圖需要在連續的雷射測距過程中獲取雷射雷達的位姿。一種常用的解決該問題的方式為使用獨立的位置估計(例如透過GPS/INS)將雷射點雲配準到一個固定的座標系統。另外的一些位置估計方法透過使用來自輪子編碼器或者視覺裏程計系統的裏程計測量來配準雷射點雲。由於裏程計累計了隨時間變化的微小增量運動,因此必定會發生漂移,更多的關註應該致力於減少累計漂移(例如使用回環檢測)。
本文考慮了使用6自由度運動的2軸雷射雷達透過低漂移的裏程計來建立地圖的情況。使用雷射雷達的一個關鍵優勢在於它對場景中的環境光照和光學紋理不敏感。雷射雷達近來的發展已經在減小它們的尺寸和重量。雷射雷達可以被人手持來穿過環境,或者裝載在無人機上。由於本文提出的方法目的在於解決與最小化裏程計漂移相關的問題,因此該方法目前沒有包含回環檢測模組。
本文提出的方法在沒有高精度測距或者慣性測量的情況下達到了低漂移且低復雜度的效能。獲取這樣效能的關鍵思想是將同時定位和建圖這個同時最佳化大量變量的典型復雜問題分離為兩種演算法(裏程計演算法和建圖演算法)。一種演算法(裏程計演算法)是實作高頻率但低精度的裏程計來估計雷射雷達速度,另一種演算法(建圖演算法)則實作低頻率但高精度的點雲匹配與配準。盡管本文提出的方法不需要IMU,但是如果有IMU可用,則可以為高頻運動提供運動先驗。具體而言,這兩種演算法提取位於邊緣和平面上的特征點,並且將特征點分別與邊緣線段和平面塊進行匹配。裏程計演算法透過快速計算來尋找特征點的匹配關系,建圖演算法透過與局部點聚類的幾何分布相關的特征值和特征向量來尋找特征點的匹配關系。
透過分解原始問題,可以獲得更簡單的問題,該問題是可以透過線上運動估計(裏程計演算法)來求解的。在此之後,建圖演算法作為批次最佳化演算法(類似於叠代最近點 ICP 方法)來得到高精度的運動估計和地圖。這種並列的演算法結構保證了問題即時求解的可行性。進一步,由於運動估計(裏程計演算法)是高頻執行的,建圖演算法就有充足時間來計算以保證精度;建圖演算法由於執行頻率較低,因此能夠包含大量特征點,並且透過足夠多的叠代次數來達到收斂。
符號約定和任務描述
本文解決的問題是透過3D雷射雷達感知到的點雲來實作自身運動估計並且建立穿行環境的地圖。需要確保雷射雷達預先標定過,同時也要保證雷射雷達的角速度和線速度是隨時間光滑且連續的,沒有發生突變。作為本文的符號約定,使用大寫的右上角標來表示座標系統,並且定義一個sweep為雷射雷達完成一次掃描收斂(即一周圈360°)。本文使用右下角標來表示第次sweep,並且使用表示第次sweep接收到的點雲。下面定義兩種座標系統:
1)雷射雷達座標系統{}是一個3D座標系統,它的原點位於雷射雷達的幾何中心。該座標系統的x軸指向左方,y軸指向上方,z軸指向前方。表示在座標系統{}中點雲中第i個點的座標;
2)世界座標系統{}是一個與雷射雷達座標系統{}在初始位置對齊的3D座標系統。表示在座標系統{}中點雲中第i個點的座標。
在上面的約定和表示下,雷射雷達裏程計和建圖問題被定義為:給定一系列的雷射雷達點雲,計算第次sweep的雷射雷達自身運動,並且透過建立穿行環境的地圖。
系統概述
A.雷射雷達硬體
本文的研究驗證於但不受限於Hokuyo UTM-30LX雷射雷達,透過它采集數據來驗證本文提出的方法。該雷射雷達具有180°的視場角,0.25°的分辨率以及40線/秒的掃描頻率,它與一個馬達連線,馬達在-90°和90°之間以180°/s的角速度控制雷射雷達旋轉。基於這樣特定的裝置,一個sweep就是從-90°到90°的一次旋轉(或者相反方向)。這裏值得註意的是,對於一個連續旋轉的雷射雷達,一個sweep僅僅只是一個半球形旋轉。一個裝載在機體上的編碼器以0.25°的角分辨率測量馬達的旋轉角度,根據旋轉角度可以將雷射點雲投影到雷射雷達座標系{}中。

B.軟體系統概述
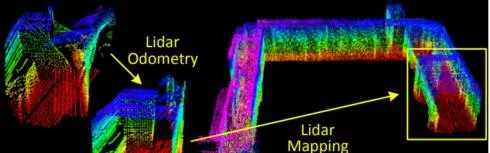
下圖為軟體系統示意圖。使用表示某一時刻雷射掃描接收到的點雲。在每個sweep中,點雲是在雷射雷達座標系{}中獲取的。將第k次sweep中所有時刻的點雲組合起來形成點雲,它在兩種演算法(裏程計演算法和建圖演算法)中進行處理。雷射雷達裏程計演算法獲取點雲,並且計算兩個連續sweep之間雷射雷達的運動,使用估計得到的運動來糾正點雲中的畸變,該演算法以10Hz頻率執行。裏程計演算法的輸出結果被雷射建圖演算法進一步處理,建圖演算法以1Hz的頻率將去畸變後的點雲與地圖進行匹配和配準。最後,將兩種演算法得到的位姿變換進行融合,以10Hz的頻率輸出融合後的雷射雷達相對於地圖的位姿變換。
雷射雷達裏程計演算法
A.特征點提取
本文從雷射雷達點雲中提取特征點開始介紹。雷射雷達自然地生成非均勻分布點雲,它在一次掃描中返回點雲結果的分辨率為0.25°,這些點雲位於一個掃描平面內。然而,當雷射雷達以180°/s的角速度旋轉並且以40Hz的頻率進行掃描時,在垂直於掃描平面方向的精度為180°/40=4.5°。根據這一事實,從點雲中提取的特征點根據共面幾何關系,僅使用來自單次掃描的資訊。 本文從邊緣線和平面小塊提取特征點。定義為點雲中的一個點,並定義為雷射雷達返回的與點在同一條掃描線上的連續點。由於雷射雷達以順時針或者逆時針順序生成點,在點兩邊各包含一半點,兩個連續點之間的間隔為0.25°。定義如下項來評估局部表面的平滑度(用來提取邊緣點和平面點):將一條掃描線上的點按值大小進行排序,將值最大的那些點作為邊緣特征點,值最小的那些點作為平面特征點。為了使環境中的特征點均勻分布,將一條掃描線劃分為4個相同子區域(程式碼中為6個子區域),從每個子區域中提取出最多2個邊緣點和4個平面點。點能夠被作為邊緣點或者平面點,若且唯若它的值大於或者小於一個閾值並且所選特征點的數量不超過設定的最大值。當選擇特征點時,一般避免在已選特征點附近進行選擇,或者避免在與雷射束大致平行的局部平面表面進行選擇(例如下圖(a)中點B),這些點通常認為是不可靠的。同樣的,也需要避免選擇遮擋區域邊界上的點作為特征點(例如下圖(b)中點A),點A被誤認為雷射雷達點雲中邊緣點,因為它的連線平面(虛線段)被其它物體所遮擋。然而,如果雷射雷達移動到另一視角下,被遮擋區域就會發生變化並且變得可觀。為了避免提取到之前提到的這些點,對中的點進行檢查,只有當形成的平面與雷射束不平行,並且中不存在比點離雷射雷達更近且與點連線在雷射束方向的點。
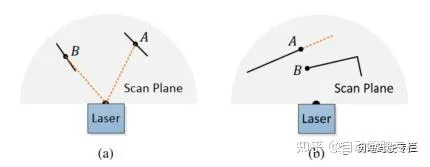
綜上所述,從最大的值開始選擇邊緣點,從最小的值開始選擇平面點,並且這些特征點還需滿足如下條件:1)所選邊緣點或者平面點的數量不超過子區域內設定的最大數量;2)已選特征點附近的點不能作為特征點;3)特征點不能在與雷射束幾乎平行的平面上,並且不能在被遮擋區域的邊界上提取。在一個走廊場景下提取特征點的範例如下圖所示,圖中邊緣點和平面點分別標記為黃色和紅色。
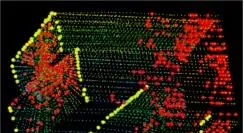
B.特征點匹配
裏程計演算法估計一個sweep中雷射雷達的運動,記為第次sweep的起始時間。在每次sweep結束的時候,將這次sweep接收到的點雲重投影到時刻,如下圖所示。將投影後的點雲記作。在下個次sweep中,和新接收到的點雲一起用來估計雷射雷達的運動。
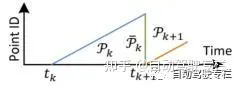
假設現在同時有和,下面開始尋找這兩個點雲之間的匹配關系。使用上一小節討論的方法提取雷射雷達點雲中的邊緣點和平面點,記和分別為提取到的邊緣點和平面點。尋找點雲中的邊緣線作為的匹配關系,以及點雲中的平面小塊作為的匹配關系。註意在次sweep開始的時候,是個空的集合,它的規模隨著掃描過程中接收到更多的點而增長。雷射雷達裏程計在sweep過程中叠代地估計自身6自由度運動。在每次叠代過程中,和使用當前估計的位姿變換投影到當前sweep的起始時刻,記和為投影後的點集。對於和中的每個點,尋找中對應的最近鄰點,這裏被儲存在3D KD樹中以實作快速索引。下圖展示了尋找邊緣點對應的邊緣線的過程,記為中的一個點,邊緣線可以用兩個點表示。記點為中離點最近鄰的點,點為中與點在不同掃描線且離點最近鄰的點。組成了與點對應的邊緣線,為了驗證和均為邊緣點,需要使用公式(1)檢查局部表面的平滑性。這裏特別要求點和點來自不同的掃描線,因為同一條掃描線不可能包含相同邊緣線上超過一個點。唯一的例外就是邊緣線就在掃描平面上,如果是這種情況,則邊緣線發生退化,並且在掃描平面上為一條直線,這樣在這條邊緣線上的特征點就不會被提取到(因為平滑性的計算是基於同一條掃描線的)。
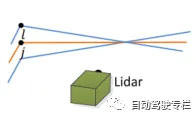
下圖展示了尋找平面點對應的平面小塊的過程,記為中的一個點,平面小塊可以用三個點表示。類似於之前尋找邊緣點對應關系,記點為中離點最近鄰的點,接著尋找另外兩個點(點和點)作為點的最近鄰點,點要求和點在同一條掃描線上,點要求在與點在相鄰的掃描線上,這樣保證了三個點非共線。為了驗證點,點和點均為平面點,再次檢查局部表面的平滑性。
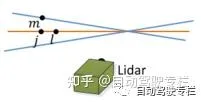
找到特征點的匹配關系後,就可以獲得計算特征點到其匹配關系的距離運算式。在下一小節中將透過最小化所有特征點距離誤差來估計雷射雷達運動。下面先從邊緣點開始,對於一個點,如果是其對應的邊緣線,則邊緣點到邊緣線的距離可以透過下式計算:其中,,和分別為雷射雷達座標系{}中點,和的座標。 對於一個點,如果是其對應的平面小塊,則平面點到平面小塊的距離可以透過下式計算:其中,為雷射雷達座標系{}中點的座標。
C.運動估計
雷射雷達在一次sweep中運動由恒定角速度和線速度來建模,這使得對於一次sweep中在不同時刻接收到的點雲可以透過線性插值位姿變換來統一到同一座標系下(點雲去畸變)。記為當前時間戳,為第次sweep的起始時間,為時間段內的雷射雷達位姿變換,它是6自由度的剛體運動,。其中,,和分別為雷射雷達座標系{}下沿,和方向的移動,,和為旋轉角度(遵循右手規則)。給定中一個點,記為它的時間戳,並且記為時間段內的雷射雷達位姿變換。能夠透過對線性插值得到:回憶上一小節,和分別是從中提取的邊緣點和平面點集合,和是投影到sweep起始時刻的點集。為了求解雷射雷達的運動,需要建立和,或者和之間的幾何關系。根據公式(4)中的變換關系,可以計算:其中,為集合和中點的座標,為集合和中對應點的座標,為中第個到第個元素,為透過羅德裏格斯公式定義的旋轉矩陣:在上式中,是旋轉向量的模長:表示旋轉方向的單位向量:是的反對稱矩陣。公式(2)和(3)計算了和中的點和它們對應關系之間的距離。根據公式(2)和公式(4)-(8),可以得到中的邊緣點和對應邊緣線之間的幾何關系:類似地,根據公式(3)和公式(4)-(8),可以建立另一個中平面點和對應平面小塊之間的幾何關系:最後,使用Levenberg-Marquardt方法求解雷射雷達的運動。根據和中每個特征點將公式(9)和公式(10)堆疊成向量形式,獲得一個非線性函式:上式中,每一行對應一個特征點,表示對應的距離。下面計算相對於的亞可比矩陣,。接著就可以透過非線性叠代最小化為0來求解公式(11):上式中,是Levenberg-Marquardt方法的一個因子。
D.雷射雷達裏程計演算法

雷射雷達裏程計演算法如上表所示。該演算法的輸入為來自上一次sweep的點雲,當前sweep中逐漸增長的點雲,以及上一次叠代的位姿變換。如果一個新的sweep剛開始,設定為0(上表中4-6行)。接著,演算法從點雲中提取特征點來構建邊緣點和平面點(上表中第7行)。對於每個特征點,尋找它在點雲中的對應關系(上表中9-14行)。在上表中第15行,演算法給每個特征點分配了平方權重,特征點和它們對應關系的距離誤差越大則分配權重越小,如果該距離誤差大於一定閾值,則認為該特征點是外點並分配權重為0。在上表中第16行,位姿變換經過一次叠代更新,如果滿足收斂條件或者超過最大叠代次數,則非線性最佳化終止。如果演算法結束了一次sweep,使用這個sweep內估計的運動將點雲投影到時間戳,否則返回位姿變換用於下一次叠代。











