基于 gpu 计算德州扑克实时 equity 曲线及转牌 equity bucket 移动
写在前面
目前的德州扑克求解器往往基于 CPU,计算时间长,并不适用于实时求解。这些求解器的原理都是遍历策略树,根据河牌的结果倒推当前的策略,因此要达到高度的准确性需要巨大的计算量。市面上的实时分析工具仅提供当前可执行的行动,没有给出玩家的详细信息供玩家决策。
因此,我希望开发一个能在短时间内根据范围绘制权益曲线的工具,并遍历所有转牌的组合,分析权益分布的变动情况,再基于经验制定行动策略。所有向量计算都将基于 GPU 上的 Torch 进行,例如使用 3060 12G 来计算 52 张牌、7 张公共牌和 1.3 亿个手牌的排序仅需要 0.05 秒。
为了计算在翻牌时两手牌的胜率,我们需要遍历 45 张翻牌和 44 张河牌,共有 990 种组合,分别计算这 990 种情况下两手牌的排名,并计算胜率。这将需要计算一个具有 1,980 行的张量。
如果计算一手牌对上整个范围的情况,不考虑手牌之间的相互影响,将需要计算一个具有 2,625,480 行的张量。
而如果计算范围对上范围的情况,同样不考虑手牌之间的相互影响,将需要计算一个具有 3,481,386,480 行的张量。
使用 torch.int8 来存储张量进行计算,仅保存这些数据就需要约 22GB 的显存,实际跑的时候以 80 手牌一个 batch, 显存占用就达到了 20 GB,range vs range 的计算一共需要17个batch,4090 计算单个 flop 仅需 10s。我没有 4090 所以我租了 4 台 4x4090,耗时约4小时,遍历了22100种翻牌情况,计算出 1326 * 1326 的 equity 矩阵。理论上来说你可以再花45倍的时间连续跑个七八天租服务器花费14k,存储空间7TB,你可以跑出所有转牌的情况,这样你也可以在毫秒级计算转牌equity了。
因此现在可以在毫秒级别绘制出翻牌 range vs range 的 equity 曲线。
1import time
2from itertools import combinations
3import matplotlib.pyplot as plt
4import numpy as np
5import poker
6from phevaluator import _evaluate_cards, sample_cards, card
7import pandas as pd
8import seaborn as sns
9import sqlite3
10import torch
11import sys
12sys.path.append('../decisionmaker')
13import evaluator
14from scipy import interpolate
15import math
准备工作
翻前策略是 8max-100std-straddle-no-ante 策略,原格式是 pioviewer 格式的,大约有 9000 多种翻前情况,提前解析好存到库里,就一个客户端就用sqlite了.
翻前策略转为 13
13
3 的numpy格式,3 的维度代表 raise allin call 的频率,然后转二进制存到数据库.
这里演示 BTN_raise_STR_3b_BTN_call 的行动线.
1# 加载策略
2conn = sqlite3.connect('../example.db')
3cur = conn.cursor()
4str_3b_query = cur.execute("select strategy_numpy from strategy where strategy_name = 'BTN_2.5strd_STR_strategy'").fetchone()
5btn_call_3b_query = cur.execute("select strategy_numpy from strategy where strategy_name = 'BTN_2.5strd_STR_11.0strd_BTN_strategy'").fetchone()
6str_3b_numpy = np.frombuffer(str_3b_query[0]).reshape((13, 13, 3))
7btn_call_3b_numpy = np.frombuffer(btn_call_3b_query[0]).reshape((13, 13, 3))
straddle 位置 AA AKs AQs AJs ATs raise allin call 的频率
1# str位置面对btn open AA的 raise allin call 频率
2print(str_3b_numpy.shape)
3print(str_3b_numpy[0,:5])
1(13, 13, 3)
2[[1. 0. 0. ]
3 [1. 0. 0. ]
4 [1. 0. 0. ]
5 [0.588 0. 0.412]
6 [0.148 0. 0.852]]
手牌的 index 对应手牌
| C | D | H | S | |
|---|---|---|---|---|
| 2 | 0 | 1 | 2 | 3 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 8 | 9 | 10 | 11 |
| 5 | 12 | 13 | 14 | 15 |
| 6 | 16 | 17 | 18 | 19 |
| 7 | 20 | 21 | 22 | 23 |
| 8 | 24 | 25 | 26 | 27 |
| 9 | 28 | 29 | 30 | 31 |
| T | 32 | 33 | 34 | 35 |
| J | 36 | 37 | 38 | 39 |
| Q | 40 | 41 | 42 | 43 |
| K | 44 | 45 | 46 | 47 |
| A | 48 | 49 | 50 | 51 |
把策略转换成所有的组合,如 AKs 转换成 AcKc AdKd AsKs AhKh 并包装成 dataframe
1# 手牌的index可视化
2def card_index_to_human(*index):
3 r = ['2', '3', '4', '5', '6', '7', '8', '9', 'T', 'J', 'Q', 'K', 'A']
4 s = ['c', 'd', 'h', 's']
5 result = [r[i // 4] + s[i % 4] for i in sorted(index, reverse=True)]
6 return "".join(result)
7
8# 手牌范围的numpy格式转换为每一个组合 如AKs就转换为 AcKc AdKd AsKs AhKh四种组合 返回一个pd.df
9# 第一列为手牌组合 第一列为扑克点数 之后为每个行动的频率
10def range_numpy_to_combo_list(player_range: np.ndarray):
11 # shape 13 13 3
12 hand_list = []
13 for row in range(13):
14 for col in range(13):
15 first_index = 4 * (12 - row)
16 first_list = list(range(first_index, first_index + 4))
17 second_index = 4 * (12 - col)
18 second_list = list(range(second_index, second_index + 4))
19 if row == col:
20 # pair
21 comb_list = list(combinations(range(4 * (12 - row), 4 * (12 - row) + 4), 2))
22 comb_list = [(tuple(sorted(t)), card_index_to_human(*t), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]) for t in comb_list]
23 hand_list = hand_list + comb_list
24 elif row > col:
25 # offsuit
26 tmp_list = []
27 for i in range(4):
28 for j in range(4):
29 if i != j:
30 tmp_list.append((tuple(sorted((first_list[i], second_list[j]))), card_index_to_human(*(first_list[i], second_list[j])), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]))
31 hand_list = hand_list + tmp_list
32 else:
33 # suit
34 tmp_list = []
35 for i in range(4):
36 for j in range(4):
37 if i == j:
38 tmp_list.append((tuple(sorted((first_list[i], second_list[j]))), card_index_to_human(*(first_list[i], second_list[j])), player_range[row][col][0], player_range[row][col][1], player_range[row][col][2]))
39 hand_list = hand_list + tmp_list
40 res = pd.DataFrame(hand_list, columns = ['hand', 'human', 'raise', 'allin', 'call'])
41 sorted_df = res.sort_values(by='hand', key=lambda x: x.apply(lambda y: (y[0], y[1]))).reset_index(drop=True)
42 return sorted_df
包装后的 combo dataframe 共 1326 行,hand 为手牌的 index tuple,然后是各个行动的频率,index 为 hand 的字典序
1%%time
2str_3b_combo_df = range_numpy_to_combo_list(str_3b_numpy)
3btn_call_3b_combo_df = range_numpy_to_combo_list(btn_call_3b_numpy)
4print(str_3b_combo_df.shape)
5str_3b_combo_df[str_3b_combo_df['raise'] > 0][:5]
1(1326, 5)
2CPU times: total: 0 ns
3Wall time: 14.6 ms
| hand | human | raise | |
|---|---|---|---|
| 241 | (4, 48) | Ac3c | 0.268 |
| 288 | (5, 49) | Ad3d | 0.268 |
| 334 | (6, 50) | Aph | 0.268 |
| 379 | (7, 51) | As3s | 0.268 |
| 383 | (8, 12) | 5c4c | 0.606 |
1%%time
2
3# 根据 flop 的牌面到库里拿到 flop equity matrix
4def get_equity_matrix_from_db(board: tuple):
5 conn = sqlite3.connect(r"E:\project_p\preflop_tips\flop_equity.db")
6 cur = conn.cursor()
7 board = "-".join([str(x) for x in board])
8 query = cur.execute(f"select flop, equity_matrix, mask_matrix from flop_equity where flop = '{board}'").fetchone()
9 conn.close()
10 equity_matrix = np.frombuffer(query[1], dtype=np.float32).reshape((1326, 1326))
11 mask_matrix = np.frombuffer(query[2], dtype=bool).reshape((1326, 1326))
12
13 return equity_matrix, mask_matrix
14
15ALL_COMBINATION = list(combinations(range(52), 2))
16def get_hand_index(hand: tuple):
17 hand = tuple(sorted(hand))
18 return ALL_COMBINATION.index(hand)
1CPU times: total: 0 ns
2Wall time: 0 ns
翻牌
要计算单个手牌对上对手范围的胜率,用自己这手牌的 index 在 equity matrix 找到所在行,用这一行乘以对手每个组合的手牌占比,然后再按行求和除以本行剔除手牌影响后的组合数,如在 9dThQh 的 flop AhAs 对上 btn_call 范围的胜率
1%%time
2# 计算单手牌的胜率
3def flop_hand_vs_range_equity(board: tuple, player_1_hand: tuple, player_2_strategy_df: pd.DataFrame, player_2_strategy: str):
4 equity_matrix, mask_matrix = get_equity_matrix_from_db(board)
5 player_1_hand_index = get_hand_index(player_1_hand)
6 player_2_strategy_df['proportion'] = player_2_strategy_df[player_2_strategy] / player_2_strategy_df[player_2_strategy][mask_matrix[player_1_hand_index]].sum()
7 player_2_strategy_df['proportion'] = np.nan_to_num(player_2_strategy_df['proportion'], nan=0.0)
8
9 return np.sum(equity_matrix[player_1_hand_index] * player_2_strategy_df['proportion'].values)
10flop_hand_vs_range_equity((29,34,42), (50, 51), btn_call_3b_combo_df, 'call')
1CPU times: total: 15.6 ms
2Wall time: 54.2 ms
3
4
5
6
7
80.7042426706000064
此函数求出双方范围内每一手牌对上对手范围的胜率和手牌在自己范围的占比
1# 范围对上范围的胜率 player_1_df新增胜率列
2def flop_range_vs_range_equity(board, player_1_strategy_df: pd.DataFrame, player_1_strategy: str, player_2_strategy_df: pd.DataFrame, player_2_strategy: str, *matrix):
3 player_1_strategy_df = player_1_strategy_df.sort_index()
4 player_2_strategy_df = player_2_strategy_df.sort_index()
5
6 if matrix:
7 equity_matrix, mask_matrix = matrix
8 else:
9 equity_matrix, mask_matrix = get_equity_matrix_from_db(board)
10 # 每手牌的权重打横之后拓展到1326行
11 p1_repeat = np.repeat(player_1_strategy_df[player_1_strategy].values.reshape(1,-1),1326,axis=0)
12 p2_repeat = np.repeat(player_2_strategy_df[player_2_strategy].values.reshape(1,-1),1326,axis=0)
13 # 权重乘以mask矩阵剔除干涉手牌
14 p1_freq = mask_matrix * p1_repeat
15 p2_freq = mask_matrix * p2_repeat
16 # 每一行权重求和
17 p1_freq_sum = np.sum(p1_freq, axis=1)
18 p2_freq_sum = np.sum(p2_freq, axis=1)
19 # 找出为0的index 避免除0
20 p1_no_zero = np.where(p1_freq_sum != 0)
21 p2_no_zero = np.where(p2_freq_sum != 0)
22 # 构建全0结果矩阵
23 p1_result = np.zeros((1326,))
24 p2_result = np.zeros((1326,))
25 # 求p1对p2的整体胜率 用equity_matrix乘以p2_freq再按行求和
26 equity_matrix_1_vs_2 = np.sum(equity_matrix * p2_freq, axis=1)
27 equity_matrix_2_vs_1 = np.sum(equity_matrix * p1_freq, axis=1)
28
29 p1_result[p2_no_zero] = equity_matrix_1_vs_2[p2_no_zero] / p2_freq_sum[p2_no_zero]
30 p2_result[p1_no_zero] = equity_matrix_2_vs_1[p1_no_zero] / p1_freq_sum[p1_no_zero]
31
32 player_1_strategy_df['equity'] = p1_result
33 player_2_strategy_df['equity'] = p2_result
34
35 player_1_strategy_df['proportion'] = 100 * (np.sum(p1_freq, axis=0) / np.sum(np.sum(p1_freq, axis=0)))
36 player_2_strategy_df['proportion'] = 100 * (np.sum(p2_freq, axis=0) / np.sum(np.sum(p2_freq, axis=0)))
37
38 player_1_strategy_df = player_1_strategy_df[player_1_strategy_df['proportion'] > 0].sort_values(by='equity', ascending=False)
39 player_2_strategy_df = player_2_strategy_df[player_2_strategy_df['proportion'] > 0].sort_values(by='equity', ascending=False)
40
41 player_1_strategy_df['cumsum'] = player_1_strategy_df['proportion'].cumsum()
42 player_2_strategy_df['cumsum'] = player_2_strategy_df['proportion'].cumsum()
43
44 # 构造cumsum 为0 y与equity max一致
45 player_1_strategy_df = pd.concat([pd.DataFrame({'cumsum': [0], 'equity': [player_1_strategy_df.iloc[0]['equity']]}), player_1_strategy_df], ignore_index=True)
46 player_2_strategy_df = pd.concat([pd.DataFrame({'cumsum': [0], 'equity': [player_2_strategy_df.iloc[0]['equity']]}), player_2_strategy_df], ignore_index=True)
47
48
49 return player_1_strategy_df, player_2_strategy_df
双方范围计算用 cpu 计算仅需 70 ms 左右,第一行空行是为了绘制 equity 曲线 x = 0 时构造起点
1%%time
2str_3b_equity_df, btn_call_3b_equity_df = flop_range_vs_range_equity((29,34,42), str_3b_combo_df, 'raise', btn_call_3b_combo_df, 'call')
3str_3b_equity_df.head()
1CPU times: total: 62.5 ms
2Wall time: 69.2 ms
| cumsum | equity | hand | human | raise | proportion | |
|---|---|---|---|---|---|---|
| 0 | 0.000000 | 0.926879 | NaN | NaN | NaN | NaN |
| 1 | 0.740942 | 0.926879 | (26, 38) | Jh8h | 0.820 | 0.740942 |
| 2 | 1.136713 | 0.916976 | (37, 46) | KhJd | 0.438 | 0.395771 |
| 3 | 1.532484 | 0.916154 | (38, 45) | KdJh | 0.438 | 0.395771 |
| 4 | 1.928255 | 0.914311 | (39, 46) | KhJs | 0.438 | 0.395771 |
绘制双方的 equity 曲线,可以看到在这个 flop 我们范围对上 btn 的范围整体上都有优势, 但是坚果优势不明显, 我们的手牌 AsAh 大概处于 30% 的位置,在 SRP 的情况下需要高频过牌,3B 底池低 spr 情况下这个区间的的手牌下注频率会升高一点
1%%time
2CARD_COMBO = list(combinations(range(52), 2))
3
4# 绘制equity曲线并标记当前手牌的位置
5def paint_equity_curve(p1_df, p2_df, *p1_hand):
6 plt.figure(figsize=(8, 6)) # 设置画布的大小
7 sns.set_palette("hls") # 设置所有图的颜色,使用hls色彩空间
8
9 plt.xlabel('Hand_rank', fontsize=15) # 添加x轴标签,并改变字体
10 plt.ylabel('Equity', fontsize=15) # 添加y轴变浅,并改变字体
11
12 plt.grid(line style='-') # 添加网格线
13
14 sns.lineplot(p1_df, x='cumsum', y='equity', color=sns.color_palette("RdBu")[4])
15 sns.lineplot(p2_df, x='cumsum', y='equity', color=sns.color_palette("RdBu")[0])
16 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 将图像的框框删掉
17 if p1_hand:
18 hand_row = p1_df[p1_df['hand'] == tuple(sorted(p1_hand[0]))]
19 plt.scatter(hand_row['cumsum'], hand_row['equity'], color='red', marker='x')
20
21 plt.show()
22paint_equity_curve(str_3b_equity_df, btn_call_3b_equity_df, (50, 51))
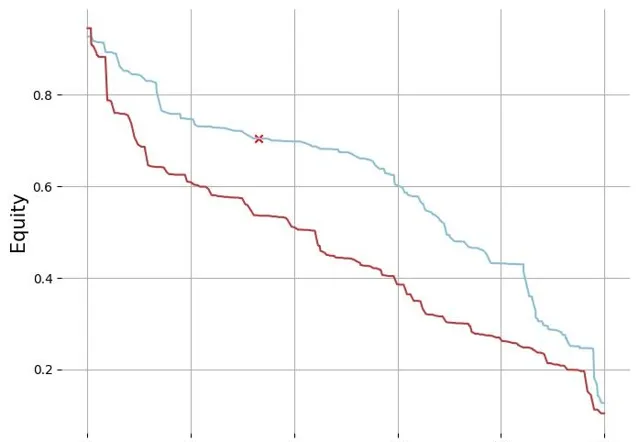
进行插值,然后分别找到两个范围的百分位点求插值后绘图,str equity 领先会在水平线以上,因为 str 的 3B 范围里是没有 KJs 的,所以 str 玩家除了在坚果范围 equity 落后于 btn 位置玩家,整体都是领先的
1%%time
2# equity差值函数
3def cal_equity_diff(p1_df, p2_df):
4 p1_df_interpolate_func = interpolate.interp1d(p1_df['cumsum'], p1_df['equity'])
5 p2_df_interpolate_func = interpolate.interp1d(p2_df['cumsum'], p2_df['equity'])
6 return p1_df_interpolate_func(list(range(100))) - p2_df_interpolate_func(list(range(100)))
7
8
9# 绘制equity_diff曲线
10def paint_equity_diff_curve(p1_df, p2_df, p1_hand=None):
11
12 diff = cal_equity_diff(p1_df, p2_df)
13 plt.figure(figsize=(8, 6)) # 设置画布的大小
14 if p1_hand:
15 is_have_hand = p1_df['hand'].loc[1:] == tuple(sorted(p1_hand))
16 if any(is_have_hand):
17 hand_row = str_3b_equity_df.loc[1:][str_3b_equity_df['hand'].loc[1:] == tuple(sorted((50,51)))]
18 plt.scatter(hand_row['cumsum'], diff[int(hand_row['cumsum'].iloc[0])], color=sns.color_palette("RdBu")[0], marker='x')
19
20
21 sns.set_palette("hls")
22 plt.xlabel('Hand_rank', fontsize=15)
23 plt.ylabel('Equity_diff', fontsize=15)
24 plt.axhline(y=0, color=sns.color_palette("RdBu")[0], line style='--')
25 plt.grid(line style='-') # 添加网格线
26 sns.lineplot(diff, color=sns.color_palette("RdBu")[4])
27 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 将图像的框框删掉
28
29
30 plt.show()
31hand = (50, 51)
32paint_equity_diff_curve(str_3b_equity_df, btn_call_3b_equity_df, hand)
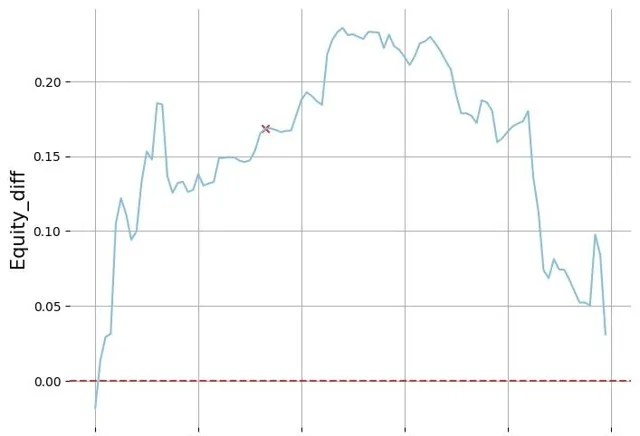
GPU torch 核心逻辑
1def evaluate_cards_input_torch(cards_tc):
2 hand_size = cards_tc.shape[1]
3 no_flush = NO_FLUSHES[hand_size]
4 hand_count = cards_tc.shape[0]
5
6 # suit_hash = torch.sum(SUITBIT_BY_ID[cards_tc], axis=1)
7 suit_hash = torch.sum(1 << (cards_tc % 4 * 3), axis=1)
8 flush_suit = (SUITS[suit_hash] - 1).reshape((hand_count, 1))
9
10 flush_suit_mask_np = torch.where(flush_suit != -1, True, False).reshape((hand_count,))
11 # 找到 card % 4 == flush_suit 这个条件的index 打标为True
12 #############################################
13 # FLUSH
14 cards_suit = cards_tc % 4
15 # [34, 30, 14, 22, 32]]
16 mask = torch.where(cards_suit - flush_suit == 0, 0x1 << (cards_tc // 4), 0) # n x 5
17 mask_t = mask.t()
18 hand_binary = mask_t[0].to(dtype=torch.int)
19 for i in range(1, hand_size):
20 hand_binary = torch.bitwise_or(hand_binary, mask_t[i])
21 hand_binary = hand_binary.t().reshape((hand_count, 1))
22 flush_result = FLUSH[hand_binary].reshape((hand_count,))
23 #############################################
24 # NO FLUSH
25 # -------------------------------------------
26 cards_rank = cards_tc >> 2
27 cards_rank_t = cards_rank.t()
28 row_counts = torch.zeros((13, cards_rank.shape[0]), dtype=torch.int8, device='cuda:0')
29 rg = torch.arange(cards_rank.shape[0], dtype=torch.int, device='cuda:0')
30 for rank in cards_rank_t:
31 row_counts[rank.to(dtype=torch.int), rg] = row_counts[rank.to(dtype=torch.int), rg] + 1
32 # -------------------------------------------
33 # 转置之后row为当前rank点数所有手牌组合的array 0 [1 0 1 1 1 1]
34 sum_numb = torch.zeros((1, row_counts.shape[1]), dtype=torch.int, device='cuda:0')
35 num_cards = torch.full((row_counts.shape[1],), hand_size, device='cuda:0')
36 full_tc = torch.full((row_counts.shape[1],), 12, dtype=torch.int, device='cuda:0')
37 for rank, row in enumerate(row_counts):
38 sum_numb = sum_numb + DP[row.to(dtype=torch.int), full_tc - rank, num_cards]
39 num_cards = num_cards - row
40 result = no_flush[sum_numb.t().reshape((hand_count,))]
41 flush = flush_result * flush_suit_mask_np
42 non_flush = result * (~flush_suit_mask_np)
43 return flush + non_flush
44
45def evaluate_fix_flop_turn_matrix(flop: tuple, player_range_1: [tuple], player_range_2: [tuple]):
46 """
47 转牌一共45张出牌,再遍历河牌44张出牌计算固定转牌下的equity matrix
48 :param flop:index tuple (12, 24, 37)
49 :param player_range_1: sorted list index tuple [(19, 26), (19, 27)...]
50 :param player_range_2: sorted list index tuple [(35, 47), (35, 48)...]
51 :return: turn card list [1, 2, 3], ever turn card equity matrix
52 """
53 # 两个玩家手牌组合的笛卡尔积
54 player_range_cartesian = [lh + rh for lh in player_range_1 for rh in player_range_2]
55 player_range_cartesian_size = len(player_range_cartesian)
56 # 方便找到(13, 45)这种手牌组合在1326个组合中的index
57 helper_index = torch.tensor(reduce(lambda x, y: x + [x[-1] + y], list(range(51, 0, -1)), [0]), dtype=torch.int,
58 device='cuda:0')
59
60 player_hands_tc = torch.tensor(player_range_cartesian, dtype=torch.int8, device='cuda:0').repeat(1, 49) \
61 .reshape(49 * player_range_cartesian_size, -1)
62
63 # 剔除掉flop3张后剩余的牌堆
64 exclude_flop_card = sorted(tuple(set(range(52)) - set(flop)))
65
66 # 构建flop river的固定组合 都是 player_range_cartesian_size * 49 行
67 river_temp_tc = torch.tensor(exclude_flop_card, dtype=torch.int8, device='cuda:0').reshape((49, 1))
68 river_tc = river_temp_tc.repeat(player_range_cartesian_size, 1)
69 flop_tc = torch.tensor(flop, dtype=torch.int8, device='cuda:0').repeat(49 * player_range_cartesian_size, 1)
70
71 # 返回 turn 和 matrix list
72 result_turn_list = []
73 result_equity_matrix_list = []
74 result_mask_matrix_list = []
75 for turn_card in exclude_flop_card:
76 result_turn_list.append(turn_card)
77 turn_tc = torch.tensor(turn_card, dtype=torch.int8, device='cuda:0').repeat(49 * player_range_cartesian_size, 1)
78 # 先不考虑手牌干涉 合并之后再剔除干涉组合
79 all_board = torch.cat((flop_tc, player_hands_tc, turn_tc, river_tc), dim=1)
80 # 剔除干涉的行
81 row_counts = torch.zeros((52, all_board.shape[0]), dtype=torch.int8, device='cuda:0')
82 rg = torch.arange(all_board.shape[0], dtype=torch.int, device='cuda:0')
83 for rank in all_board.t():
84 row_counts[rank.to(dtype=torch.int), rg] = row_counts[rank.to(dtype=torch.int), rg] + 1
85 # 剔除干涉后hand vs hand river一共有44种出牌
86 interference_mask = ~(torch.max(row_counts, dim=0).values > 1) # 无效置false
87 all_board = all_board[interference_mask]
88
89 player_rank_1 = evaluate_cards_input_torch(all_board[:, [0, 1, 2, 3, 4, 7, 8]])
90 player_rank_2 = evaluate_cards_input_torch(all_board[:, [0, 1, 2, 5, 6, 7, 8]])
91
92 # 每一行为一个组合对上一个组合的胜率
93 single_turn_greater_equity = torch.sum(((player_rank_1 - player_rank_2) < 0).reshape(-1, 44), dim=1) / 44
94 single_turn_equal_equity = 0.5 * torch.sum(((player_rank_1 - player_rank_2) == 0).reshape(-1, 44), dim=1) / 44
95
96 single_turn_greater_equity_t = torch.sum(((player_rank_2 - player_rank_1) < 0).reshape(-1, 44), dim=1) / 44
97 single_turn_equal_equity_t = 0.5 * torch.sum(((player_rank_2 - player_rank_1) == 0).reshape(-1, 44), dim=1) / 44
98 del player_rank_1
99 del player_rank_2
100 base_matrix = torch.zeros((1326, 1326), dtype=torch.float32, device='cuda:0')
101 mask_matrix = torch.zeros((1326, 1326), dtype=torch.int8, device='cuda:0')
102
103 all_board = all_board.reshape(-1, 44, 9)
104
105 base_matrix[
106 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1,
107 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1] \
108 = single_turn_greater_equity + single_turn_equal_equity
109 base_matrix[
110 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1,
111 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1] \
112 = single_turn_greater_equity_t + single_turn_equal_equity_t
113 mask_matrix[
114 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1,
115 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1] \
116 = 1
117 mask_matrix[
118 helper_index[all_board[:, 0, 5].to(dtype=torch.int)] + all_board[:, 0, 6] - all_board[:, 0, 5] - 1,
119 helper_index[all_board[:, 0, 3].to(dtype=torch.int)] + all_board[:, 0, 4] - all_board[:, 0, 3] - 1] \
120 = 1
121
122 result_equity_matrix_list.append(base_matrix)
123 result_mask_matrix_list.append(mask_matrix)
124
125 return result_turn_list, result_equity_matrix_list, result_mask_matrix_list
转牌
遍历转牌的所有出牌大概需要3s,计算出每个转牌的 equity df,绘制每个转牌的 euiqty 曲线,观察曲线变化情况
1%%time
2turn_list, equity_matrix_list, mask_matrix_list = evaluator.evaluate_fix_flop_turn_matrix((29, 34, 42), str_3b_equity_df.sort_index()['hand'][1:], btn_call_3b_equity_df.sort_index()['hand'][1:])
1CPU times: total: 2.73 s
2Wall time: 2.91 s
1%%time
2p1_stg_df_list = []
3p2_stg_df_list = []
4
5for index, turn_card in enumerate(turn_list):
6 p1_stg_df, p2_stg_df = flop_range_vs_range_equity((29, 34, 42), str_3b_combo_df, 'raise', btn_call_3b_combo_df, 'call',*(equity_matrix_list[index].cpu().numpy(), mask_matrix_list[index].cpu().numpy()))
7 p1_stg_df['turn'] = turn_card
8 p2_stg_df['turn'] = turn_card
9 p1_stg_df_list.append(p1_stg_df)
10 p2_stg_df_list.append(p2_stg_df)
1CPU times: total: 1.36 s
2Wall time: 1.61 s
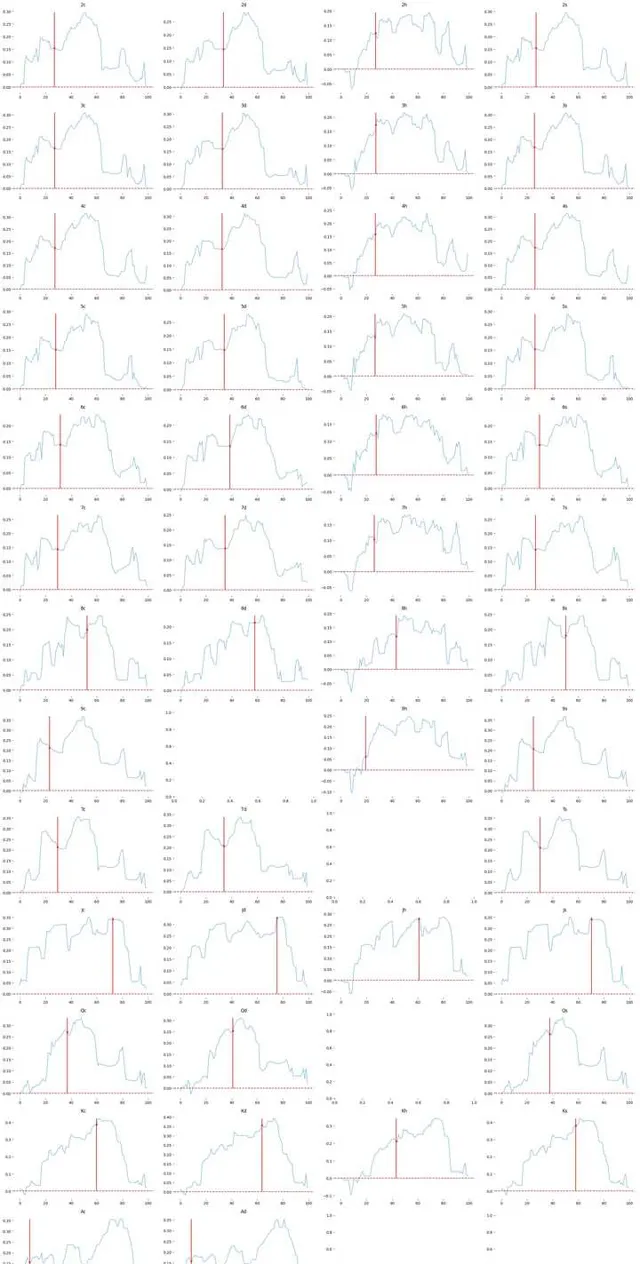
绘制所有转牌出牌的 equity diff 曲线,每一列代表不同花色,每一行代表不同rank,可以看到转牌成花之后我们的坚果优势完全丧失,对方的顶端范围大量的Ax Kx同花,而在发 8 J K 之后我们的手牌由原来的 30% 区间段后移到 40-60% 区间段,同花顺面甚至到 60% 区间段之后.
所有的转牌只有 A 是对我们有帮助使我们手牌的 equity 位置前移的,所以在我看来 AA 在这个 flop 需要高频下注来阻止对手实现转牌的 equity
1hand = (50, 51)
2fig,axes=plt.subplots(13,4, figsize=(24, 49))
3
4for index in range(49):
5 if hand[0] != turn_list[index] and hand[1] != turn_list[index]:
6 diff = cal_equity_diff(p1_stg_df_list[index], p2_stg_df_list[index])
7 sns.set_palette("hls") # 设置所有图的颜色,使用hls色彩空间
8 hand_row = p1_stg_df_list[index].loc[1:][p1_stg_df_list[index]['hand'].loc[1:] == tuple(sorted(hand))]
9 sns.scatterplot( x=hand_row['cumsum'], y=(diff[math.ceil(hand_row['cumsum'].iloc[0])] + diff[math.ceil(hand_row['cumsum'].iloc[0]) - 1]) / 2,color=sns.color_palette("RdBu")[0],ax=axes[turn_list[index]//4, turn_list[index]%4])
10 sns.lineplot(diff, color=sns.color_palette("RdBu")[4], ax=axes[turn_list[index]//4, turn_list[index]%4]).set_title(card_index_to_human(turn_list[index]))
11 axes[turn_list[index]//4, turn_list[index]%4].axhline(y=0, color=sns.color_palette("RdBu")[0], line style='--')
12 axes[turn_list[index]//4, turn_list[index]%4].set_xlabel("")
13 axes[turn_list[index]//4, turn_list[index]%4].vlines(x=hand_row['cumsum'], ymin=0, ymax=max(diff), color="red")
14 sns.despine(ax=None, top=True, right=True, left=True, bottom=True) # 将图像的框框删掉
15
16
17plt.tight_layout()
18plt.show()
后续工作
- 目前已经完成了基于 WPK 的翻前提示,但是没有根据 bet size 来调整翻前范围,后续会根据对手尺度来调整双方范围
- 转牌的计算逻辑还有优化空间,12GB 显存计算 SB VS BB 策略范围太大不分 batch 还是跑不出来
- 绘图只是方便人类归纳总结,具体策略后续考虑用 RL 来跑,而目前所作的工作可以通过参数喂给它
- 根据 position,spr,equity bucket move 这几个参数来制定翻后策略
- 感兴趣的小伙伴私信联系啊











