一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A、B、C、D四个选项,其中只有一个是正确的。
1.(4分)近年来我国芯片技术迅猛发展,麒麟系列芯片突破封锁,采用先进的7纳米工艺.7纳米=0.000007毫米,将数据0.000007用科学记数法表示为
故选:D.
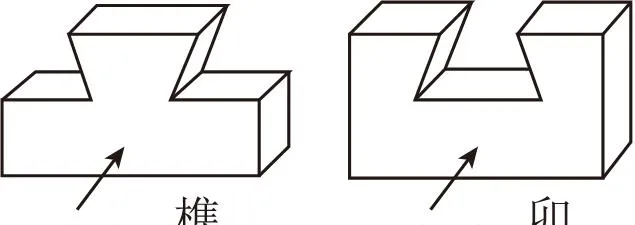
3.(4分)榫卯(sǔnmǎo),是古代中国采用凹凸部位相结合的一种连接方式.在物件上不使用钉子,利用榫卯加固物件,体现出中国古老的文化和智慧.如图是某种榫卯构件的示意图,则它们的
A.
B.
C.
D.
∴不等式组的解集为:﹣3≤x<1,
故选:B.
5.(4分)如图,AB∥DE,∠ABC=80°,∠C=40°,则∠CDE=
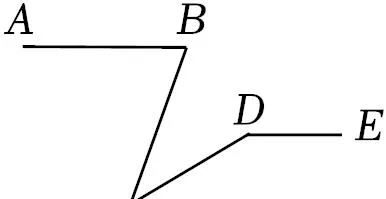
A.120°B.130°C.140°D.150°
【解答】解:延长ED交BC于F,
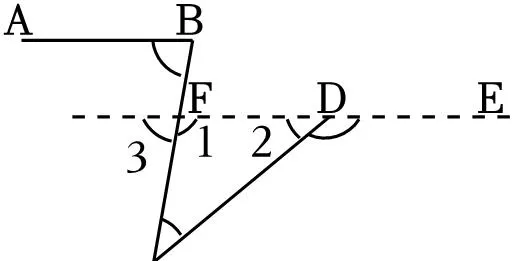
∵AB∥DE,
∴AB∥EF,
∴∠3=∠ABC=80°,
∴∠1=180°﹣∠3=180°﹣80°=100°,
∴∠CDE=∠C+∠1=40°+100°=140°,
故选:C.
【解答】解:根据题意可得:x⊗(x+2)=x(x+2)﹣x,6⊗x=6x﹣6,
∵x⊗(x+2)=6⊗x,
∴x(x+2)﹣x=6x﹣6,
故选:B.
7.(4分)在皖文中学组织举办的「唐风宋韵」诗词大赛中,九年级参赛的25名同学的成绩情况如统计图所示,这些成绩的众数和中位数分别是
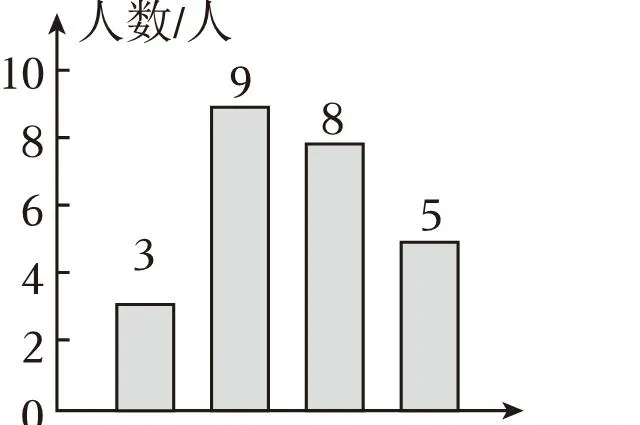
A.98,97B.98,96C.96,98D.96,97
【解答】解:由图可知:98出现的次数最多,故众数为98,
按照从小到大排列,第13个数据为96,故中位数为96;
故选:B.
8.(4分)已知四边形ABCD,对角线AC和BD交于点O,则下列命题是真命题的是
A.如果OB=OD,∠ABC=∠ADC,那么四边形ABCD为平行四边形
B.如果AB=CD,OB=OD,那么四边形ABCD为平行四边形
C.如果AD∥BC,∠ADB=∠CBD,那么四边形ABCD为平行四边形
D.如果AB∥CD,∠ABC=∠ADC,那么四边形ABCD为平行四边形
【解答】解:A、如果OB=OD,∠ABC=∠ADC,不能判定四边形ABCD为平行四边形,故本选项不符合题意;
B、如果AB=CD,OB=OD,不能判定四边形ABCD为平行四边形,故本选项不符合题意;
C、如果AD∥BC,∠ADB=∠CBD,不能判定四边形ABCD为平行四边形,故本选项不符合题意;
D、如果AB∥CD,则∠ABC+∠BCD=180°,再由∠ABC=∠ADC,可得∠ADC+∠BCD=180°,则得到AD∥BC,那么四边形ABCD为平行四边形,故本选项符合题意,
故选:D.
A.B.
C.D.
∴抛物线与x轴相交于(0,0),(2,0),
∴抛物线开口向上,
∴抛物线图象经过第一、二、四象限,
∴双曲线图象位于一、三象限,
∴抛物线与双曲线交点位于第一象限,即a>0,
∴y=ax+2﹣a必过一、三象限,
∵抛物线与x轴相交于(0,0),(2,0)
∴由图可知,抛物线与双曲线交点在(2,0)右边,
∴a>2,
∴2﹣a<0,
∴直线y=ax+2﹣a的图象经过一、三、四象限,
故选:A.
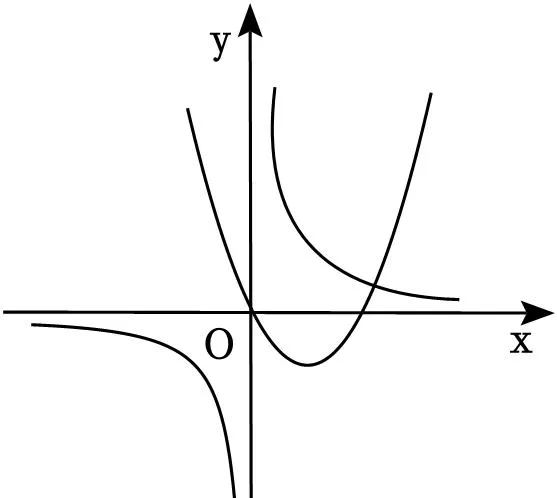
A.CD的最大值是4B.当DE⊥EF时,DE=2
C.CD的最小值是2D.当DE=2时,DE⊥EF
【解答】解:A、如图:EF,OC相交于点H,连接OE,
∵直线AB与⊙O相切于点C,
∴AB⊥OC,
∵EF∥AB,
∴EF⊥OC,
∵
∴
∴OC=2,
当点C、O、D在同一条直线上时,CD取最大值,此时CD=2OC=4,
故A正确,不符合题意;
C、∵EF⊥OC,
∴CE=CE,
∴∠COF=∠COE=60°,
∵OC=OF=2,
∴△COF是等边三角形,
∴CF=2,
当点D在CF上时,CD<CF,即CD<2,
故C不正确,符合题意;
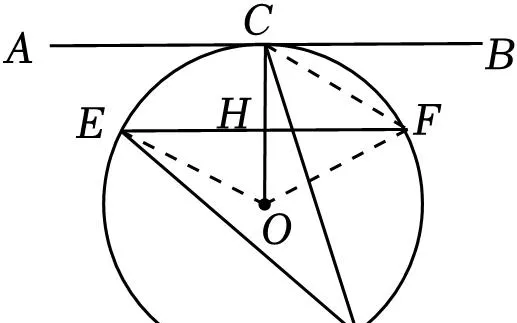
B、连接DF,OD,
∵∠COF=∠COE=60°,OE=OF,
∴∠OFE=30°,
当DE⊥EF时,∠DEF=90°,
∴DF为直径,则DF=4,
∵OF=OD=2,
∴OF+OD=DF,即点D、O、F共线,
∴∠DFE=30°,
故B正确,不符合题意;
D、当DE=2时,
∵DE=OE=OD=2,
∴△DOE是等边三角形,则∠DEO=60°,
∴∠OEF=30°,
∴∠DEF=90°,即DE⊥EF,
故D正确,不符合题意;
故选:C.
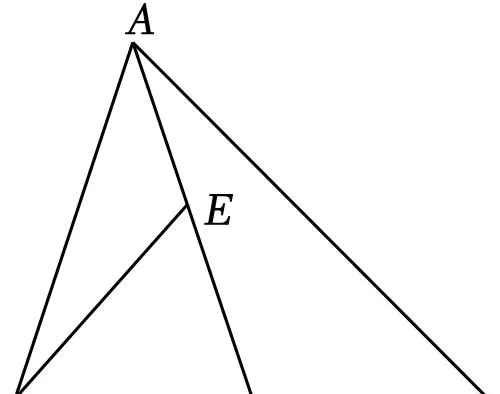
【解答】解:∵AD是中线,BC=6,
∴BD=CD=3,
∵BE=BD,
∴BE=3,∠BED=∠BDE,
∵∠BED=∠ABE+∠BAE,∠BDE=∠DAC+∠C,∠ABE=∠DAC,
∴∠BAE=∠C,
又∵∠ABD=∠CBA,
∴△ABD∽△CBA,
解得:(负值已经舍去).
故答案为:.
∴抛物线对称轴为直线x=2,
∴点A离对称轴的距离小于点B离对称轴的距离,
∵a<0,
∴抛物线开口向下,
∴离对称轴越远函数值越小,
故答案为:>;
解得x=1或x=4,
∴x 1 =1,x 2 =4,
∵y 1 ﹣y 2 <3,
∴a+k﹣(4a+k)<3,
∴a>﹣1且a≠0,
故答案为:a>﹣1且a≠0.
=
=
=
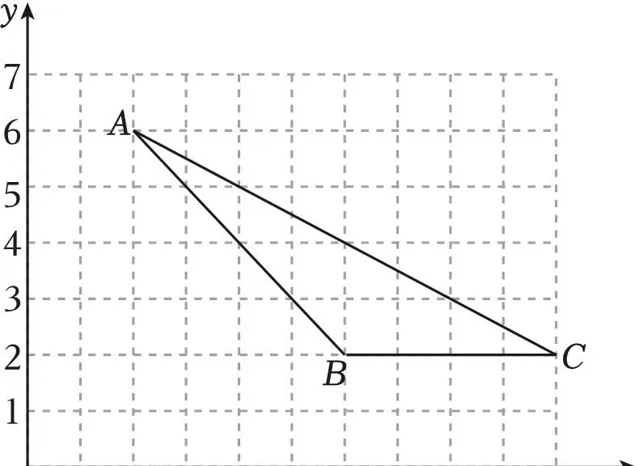
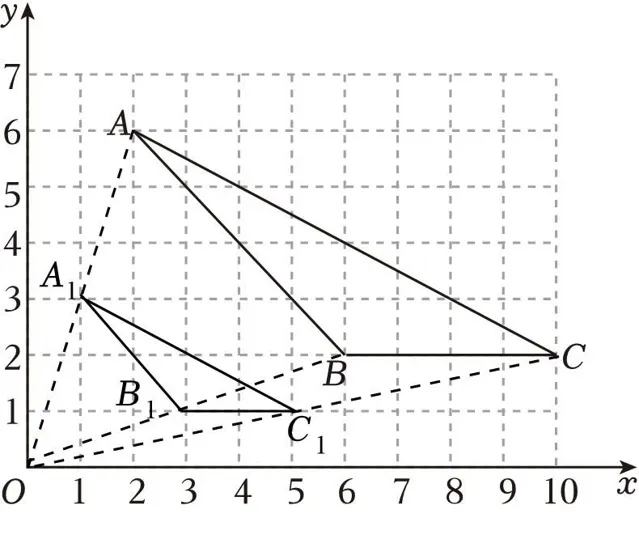
16.(8分)已知△ABC在平面直角坐标系中的位置如图所示,其中点A和点B的坐标分别为A(2,6),B(6,2).
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)某健身达人今年2月份在网上开通直播分享健身经验和健康饮食,吸引了大批粉丝.2月份新增关注人数为10万人,4月份新增关注人数为14.4万人.
(1)求2月份到4月份该健身达人直播的新增关注人数的月平均增长率;
(2)如果能保持这个月平均增长率,则接下来哪一个月该健身达人直播的新增关注人数能达到20万人?
【解答】解:(1)设新增关注人数的月平均增长率为x,
答:2月份到4月份该健身达人直播的新增关注人数的月平均增长率为20%;
(2)5月份新增关注人数为:14.4×(1+20%)=17.28(万人),
6月份新增关注人数为:17.28×(1+20%)=20.736(万人),
答:6月该健身达人直播的新增关注人数能达到20万人.
18.(8分)邻边不相等的矩形纸片,剪去一个正方形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个正方形,又余下一个四边形,称为第二次操作;……依次类推,若第n次操作余下的四边形是正方形,操作停止,这样第n次操作后所得到的余下的正方形则称为原矩形的n阶正方形,如图,相邻两边长分别为3和5的矩形,最后所得到的正方形为原矩形的3阶正方形.

(1)完成上表:
(2)已知矩形的两相邻边长分别为a,b,满足a=6b+m,b=3m(m为正整数),则最后所得到的正方形是原矩形的 8阶正方形.
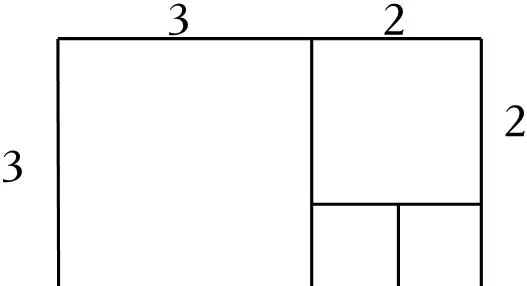
【解答】解:(1)矩形相邻的两边长为3和2时,操作次数为2,最后所得到的正方形为原矩形的2阶正方形;
当矩形相邻的两边长为8和3时,如图:
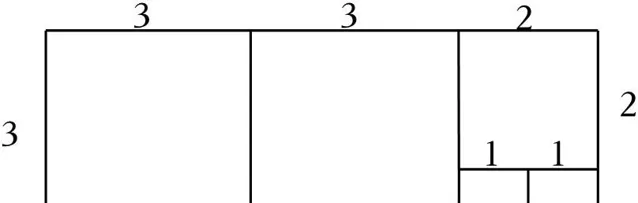
操作次数为4,最后所得到的正方形为原矩形的4阶正方形;
填表如下:

(2)a=6b+m,b=3m,
∴a=19m,
如图:

经过8次操作,最后所得到的正方形为原矩形的8阶正方形;
故答案为:8.
五、(本大题共2小题,每小题10分,满分20分)
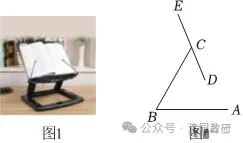
【解答】解:如图,过点E作EF⊥AB于点F,过点C作CG⊥EF于点G.
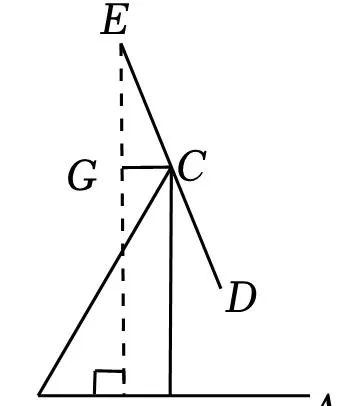
∴四边形CGFH为矩形,
∴GF=CH,EF∥CH,
∴∠CEG=∠DCH.
∵∠ABC=60°,BC=16cm,
∴∠CEG=∠DCH=∠BCD﹣∠BCH=52°﹣30°=22°.
∵C是DE的中点,
∴
∴
∴EF=EG+GF=7.5+13.84≈21.3cm,即支撑板上的点E到底面AB的距离是21.3cm.
(1)求k,b的值;
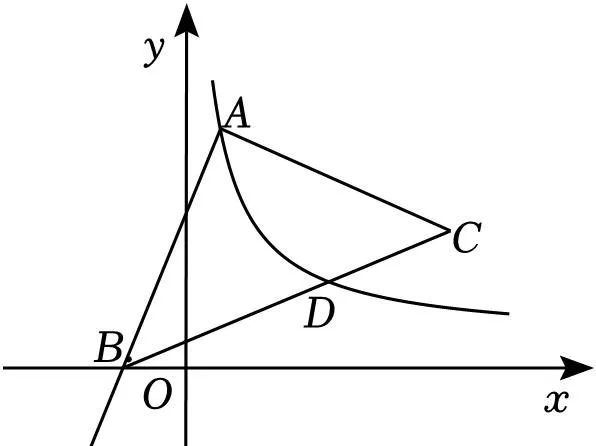
【解答】解:(1)把B(﹣2,0)代入y=2x+b得:0=2×(﹣2)+b,
解得:b=4,
∴该直线的函数解析式为y=2x+4,
把A(m,6)代入y=2x+4得:6=2m+4,
综上:k=6,b=4.
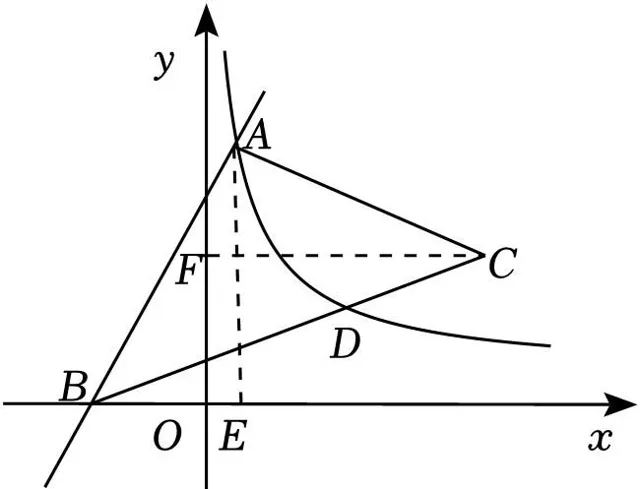
(2)过点A作AE⊥x轴于点E,过点C作CF⊥AE与点F,
∵A(1,6),B(﹣2,0),
∴AO=6,OB=3,
∵AE⊥x轴,CA⊥AB,
∴∠OAB+∠FAC=90°,∠OAB+∠OBA=90°,
∴∠FAC=∠OBA,
∵AE⊥x轴,CF⊥AE,
∴∠AFC=∠BOA=90°,
在△AOB和△CFA中,
∴△AOB≌△CFA,
∴AF=OB=3,AO=CF=6,
∴C(7,3),
设BC所在直线的函数解析式为y=mx+n,
将B(﹣2,0),C(7,3)代入得:
联立
则
六、(本题满分12分)
21.(12分)为了了解白龙村村民家庭的用电情况,电力公司抽样调查了该村村民的每月每户用电的电费,根据调查结果,绘制出了如下两个尚不完整的统计图表.请根据图表,解答下列问题:
白龙村村民用电情况抽样调查统计表

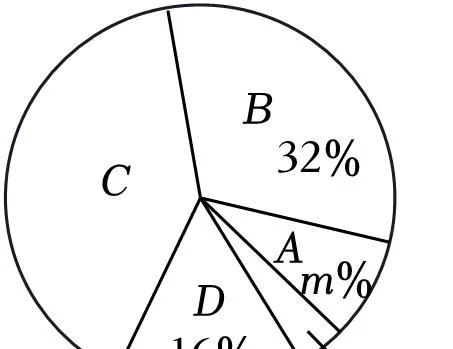
白龙村村民用电情况抽样调查扇形统计图
(1)填空:这次被调查的户数共有 50户,a+b=28,m=8;
(2)扇形统计图中扇形C的圆心角度数为 144°;
(3)电力公司拟从小刘、小陈等五名工作人员中任选两位前往白龙村进行用电安全检查和指导科学用电,求小刘和小陈至少有一人被选中前往该村的概率.
∴m=8;
故答案为:50,28,8;
(2)360°×(1﹣32%﹣8%﹣4%﹣16%)=144°;
故答案为:144°;
(3)分别用A,B,C,D,E表示小刘、小陈和其他三名工作人员,画出树状图如图:
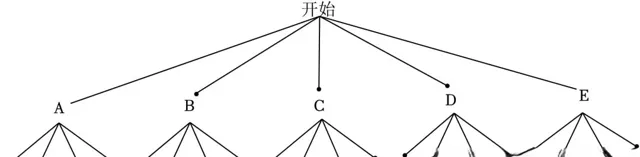
共有20种等可能的结果,其中小刘和小陈至少有一人被选中有14种等可能的结果,
七、(本题满分12分)
(1)求p关于x的函数关系式;
(2)求等待观光车的游客最多时有多少人?
当5<x≤8时,p=50x+1550﹣20x×12=﹣190x+1550,
∵a=﹣20<0,
∴当x=4时,p有最大值620;
当5<x≤8时,p=﹣190x+1550,
把x=5代入得,p=﹣190×5+1550=600,
∵k=﹣190<0,
∴p最大值小于600,
综上:等待观光车的游客最多时有多少人620人.
八、(本题满分14分)
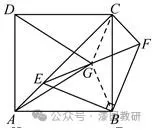
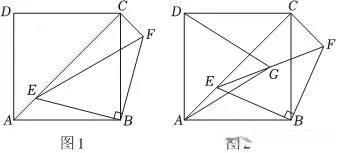
23.(14分)如图1,点E是正方形ABCD的对角线AC上一个动点(不与A,C重合),连接BE,作等腰直角△EBF,其中∠EBF=90°,EF与BC相交,连接CF.
(1)求证:△ABE≌△CBF;
(2)如图2,点G为EF的中点,连接DG,AG,DG=DC.
①△ADG是什么特殊三角形,并说明理由;
②线段BE与CF之间的有什么数量关系,并证明你的结论.
【解答】解:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△EBF是等腰直角三角形,
∴BE=BF,∠EBF=90°,
∴∠ABC﹣∠EBC=∠EBF﹣∠EBC,即∠ABE=∠CBF,
在△ABE和△CBF中,
∴△ABE≌△CBF(SAS);
(2)①连接CG,BG,
∵四边形ABCD是正方形,
∴∠BCA=∠BAC=45°,
∵△ABE≌△CBF,
∴∠BCF=∠BAC=45°,
∴∠ECF=∠BCA+∠BCF=90°,
∵点G为EF的中点,∠EBF=90°,
∴∠GCB=∠GBC,
∴∠GCD=∠GBA,
在△DCG和△ABG中,
∴△DCG≌△ABG(SAS),
∵DG=DC,AD=CD,
∵△ADG是等边三角形;
∴∠GCB=90°﹣∠DCG=15°,
∵点G为EF的中点,∠EBF=90°,
∴△CGF是等边三角形,
∴GE=GF=x,则EF=2x,
∵△EBF是等腰直角三角形,