东京奥运会的乒乒球比赛已经接近尾声,激烈的团体赛即将进行最后的争夺!(中国队加油!)

赛场上,运动员们通过不同的发球和接球手法,使得乒乓球在球拍和球桌上交替发出乒乓之声,形成了激烈的对抗。那么,比赛对抗的难度、选手技法的高低是通过什么表现出来的呢?
答案就是——乒乓球的前进速度和旋转强度。
运动员出球速度快,留给对手的反应时间就短,能打得对手措手不及;同时,通过不同速度大小和方向出球,能够形成不同的落点,逼迫对方频繁进行前后、左右的移动来应对;为了增加还击难度,还可以在出球时加上各种旋转,增大对方回球时的失误概率。

如果用物理老师的话来讲:乒乓球是在重力场中,球体与空气、球拍和球桌发生相互作用的六自由度运动,包括三个平动和三个转动自由度。其中, 乒乓球和球拍的相互作用是关键 (嘭嘭嘭,老师敲黑板了!)。
那么 ,高手打的球为什么能拐弯?乒乓球是如何转起来的?
乒乓球的旋转奥秘——静摩擦
球拍与乒乓球在碰撞过程中,除了发生正碰外(法向的撞击力过球心),球拍相对于乒乓球的切向挥动还会引发相互摩擦力,并使球体发生转动。故球拍传递给球的力是撞击力与摩擦力的合力,前者改变球体的速度方向和大小,后者改变球体的转动方向和大小。
如果没有摩擦力,就不能发生旋转,这也是「光板」球拍时代打不出像样旋转球的原因。
从二十世纪五十年代开始,能产生摩擦力的 反贴胶球拍 出现,亚洲选手的「弧圈球」一举横扫欧洲,令世界乒坛「谈弧色变」。
1981年第36届世乒赛上,中国选手蔡振华在决胜局紧要关头,以不同旋转发球的技法连得5分,战胜盖尔盖伊。
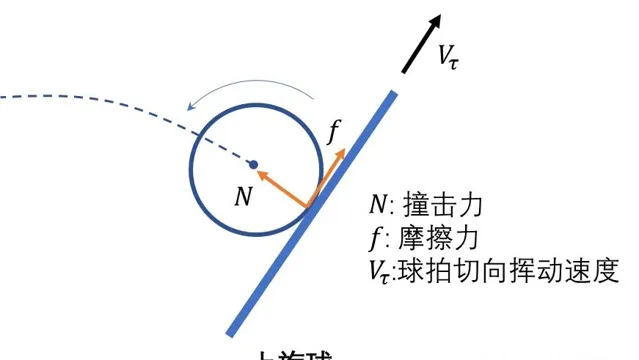
而为了达到可控的旋转,就要避免在球拍和乒乓球碰撞过程中出现滑动摩擦,让整个过程处于静摩擦力的作用范畴,也就是要使乒乓球旋转起来的切向速度与球拍的切向挥动速度一致。
静摩擦力与两个因素有关,一个是撞击力的大小,一个是球拍「粘性」的大小(就是摩擦力系数啦)。
因此,使得旋转可控的途径就有两个:第一,增大击球时的出球速度,挥拍越快,拍与球之间的摩擦力越大;第二,提高球拍的「科技」含量,比如利用反贴胶材质和正胶颗粒顶端的细小花纹,或刷胶灌油等技术提高球拍的「粘性」。
如今,花样百出的旋转已经成为赛场上的基本「杀伤」手段。
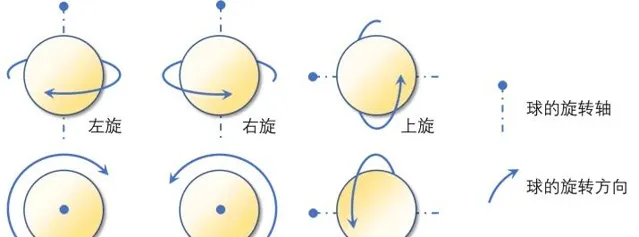
乒乓球的旋转通常分为六大类:上旋球、下旋球、左旋球、右旋球、顺旋球和逆旋球。
当乒乓球体远离击球者时,后半部分向上旋转为上旋球,向下为下旋球;向左为左侧旋球,向右为右侧旋球;顺时针旋转为顺旋球,逆时针为逆旋球。正常比赛中乒乓球的旋转大多是两个旋转结合的,比如左上旋球。
除了怎么转起来的,再附赠一个怎么拐弯的回答……那些「反直觉」的弧圈球是怎么打出来的?
那么,乒乓球的旋转是如何带来「杀伤」力的呢?是什么令旋转的乒乓球如此「不可捉摸」?
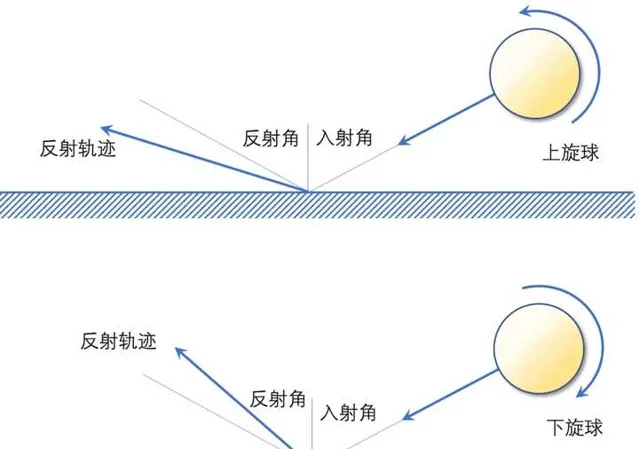
当一个旋转球与桌面或球拍发生碰撞时,除了撞击力外还会有摩擦力。在与桌面的碰撞时,如果没有旋转,乒乓球会在撞击力作用下反弹,摩擦力几乎可以忽略,反射角基本与入射角相等。 如果乒乓球有旋转,那它与桌面碰撞时的摩擦力会使得反射角发生改变。
比如,上旋球与桌面碰撞时,将产生前进方向的摩擦力,使得球体弹起时向前猛冲,反射角大于入射角;下旋球则相反,受到向后的摩擦力,使得反射角小于入射角,甚至可能在前进速度不大而下旋极强时,产生「回跳」现象。
当接球者的球拍和上旋球接触时,摩擦力会使球沿着拍面「上爬」而增大反弹角度;下旋球则沿着拍面「下钻」而减小反弹角度。 这就是回击上旋球时经常出现「远走高飞」,应付下旋球时容易「自投罗网」的道理。
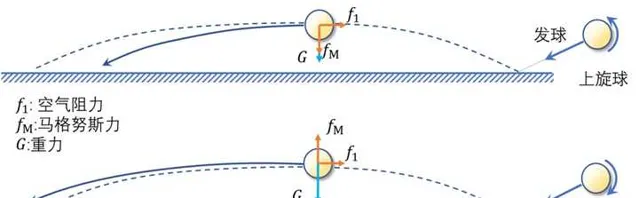
旋转的乒乓球不仅在落台和触拍时会让人感到「反直觉」,它在空中飞行的路径也会同样「反直觉」。 显然,空中飞行的乒乓球路径的改变是与空气的粘性有关的,这就需要咱们请出空气动力学来解释了。
一方面,空气的粘性使得乒乓球飞行受阻,前进速度越快,空气阻力越大。粗略地估算,阻力与速度的平方成正比,这使得乒乓球的飞行并非抛物线轨迹。
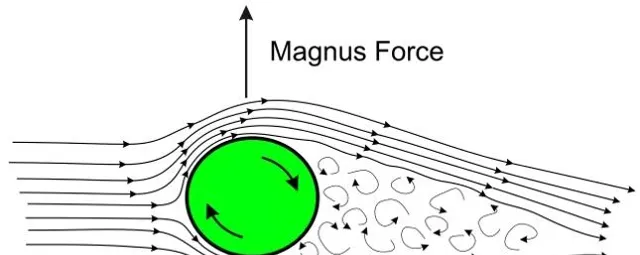
另一方面,旋转的乒乓球还会带动周围空气旋转,使得一侧空气速度增加,另一侧速度减小,形成非对称的气流。
如果旋转角速度方向与前进方向不重合(嘭嘭嘭,老师又敲黑板了!),乒乓球将受到一个「既垂直旋转角速度方向,又垂直于前进方向」的横向力,使飞行弧线发生偏移。若是上旋球,则产生向下的力,使得飞行弧线变低;反之,下旋球的飞行弧线升高;而侧旋球则朝左右方向飘飞。
在流体力学中,旋转物体运动产生的横向力被称为马格努斯力(Magnus Force),而这一现象则被称为马格努斯效应[1]。 由于空气阻力和马格努斯力的存在,飞行速度的大小和方向发生会发生「反直觉」般的非线性改变,这也是传说中「弧圈球」的来由。
马格努斯效应不仅为「乒乓必杀技」提供了方法论,更在网球、棒球、排球、篮球等中都有应用,足球项目中著名的「香蕉球」也是这个原理。
另外,马格努斯效应还对旋转炮弹、导弹的设计和制导控制等有重要意义。
当我们熟悉了这些力学常识后,就能更加「胸有成竹」地与旋转球周旋,感受乒乓球比赛优美而错落的节奏感,欣赏乒乓球「反直觉」带来的「确定性」。
参考资料
[1]Kármán, Theodore von (1963): Aerodynamics: McGraw-Hill Education.
[2]https:// funsizephysics.com/spin s-and-skyrmions/
作者:余永亮(中国科学院大学)
出品:科学大院
转载请联系[email protected]
后记: 这篇文章发布2小时后,余老师就被拉进了力学所的乒协群,并收到了战书: