作为文学作品,很难做到滴水不漏。但总体设定有据可循。通过将三维欧氏空间下的已有规律进行扩展,并增加一些假设,我们能够对四维欧氏空间的简单场景进行渲染。这个回答将实现这部分工作。
首先来回顾一下【三体III 死神永生】中对四维视角下场景的描写:
此时,莫沃维奇和关一帆的眼前,「蓝色空间」号飞船像一幅宏伟的巨画舒展开来。他们可以一直看到舰尾,也可以一直看到舰首。他们能够看到每一个舱室的内部,也能够看到舱中每一个封闭容器的内部;可以看到液体在错综复杂的管道中流动,看到舰尾核反应堆中核聚变的火球……当然,透视原理仍然起作用,太远就看不清楚,但一切都能看到。没有这种经历的人在听他们描述时会产生一个错误的印象,感觉他们是「透过」舰体看到所有的一切,事实是他们没有「透过」什么,一切的一切都并列在外,就像我们看一张纸上画的圆圈,能看到圆圈内部,并没有「透过」什么。这种展开是所有层次上的,最难以描述的是固体的展开,竟然能够看到固体的内部,比如舱壁或一块金属、一块石头,能看到它们所有的断面!他们被视觉信息的海洋淹没了,仿佛整个宇宙的所有细节全聚集在周围色彩斑斓地并列呈现出来。这时,他们不得不面对一个全新的视觉现象:无限细节。
因为最近有接触光线追踪相关的项目,之前又有机器人学相关背景。当时看到这个章节,就打算试着把四维视角下的场景用光线追踪渲染出来试试。因为三维欧氏空间(Euclidean Space)的刚体运动在机器人学中已经有非常成熟的表述,刚体位姿(Pose)可以分解为位置(Position)和姿态(Orientation)。通过对三维位姿的扩展,应该不难模拟刚体在四维欧氏空间中的运动。而渲染出四维空间中的图像,需要借助计算机图形学的方法。现在流行的光线追踪(Ray Tracing)技术遵照物理学规律对光线在空间中的传播进行模拟,然后对场景的图像进行渲染。而且相比光栅化的方法(Rasterization)实现简单,经过简单地修改也不难推广到四维欧氏空间。
预备知识:光线追踪(Ray Tracing)
光线追踪最基本的思想是逆向的模拟光线传播的过程。虚拟的光线从相机出发,由计算机检测射线和场景内物体的碰撞。按照碰撞对象的材质、颜色等纹理信息,对光线进行折射、反射以及衰减。由于一副图片上的每一个像素都对应着至少一束光线,而且光线需要多次反射才能达到较好的渲染效果,因此光线追踪的运算量巨大,往往难以用于实时渲染。github上有一个非常经典的光线追踪教程:一个周末实现光线追踪(Ray Tracing in One Weekend) [1] 。我在原作者的基础上做了一些修改,引入了一些基本的第三方库,使得这个精简版CPU光线追踪引擎能够渲染一些带纹理的三角形网格(Triangle Mesh)模型。用贝塞尔曲线简单地拉了一个「水滴」的轮廓,测试了下渲染结果:

完善了三维光线追踪引擎的基本功能后,接下来就是考虑如果把维度从三维扩展至四维。
四维相机与三维「视网体」
在扩展四维视觉前,有必要对三维世界的针孔相机(Pinhole Camera)模型进行简单地介绍。人类能通过二维的视网膜感受到三维的世界,能通过相机将三维世界的美好瞬间记录在二维的像素平面内,都借助了针孔相机模型。眼睛的晶状体或者相机的镜片组将三维世界的光线投射在二维的成像平面上,损失了一个轴的信息。
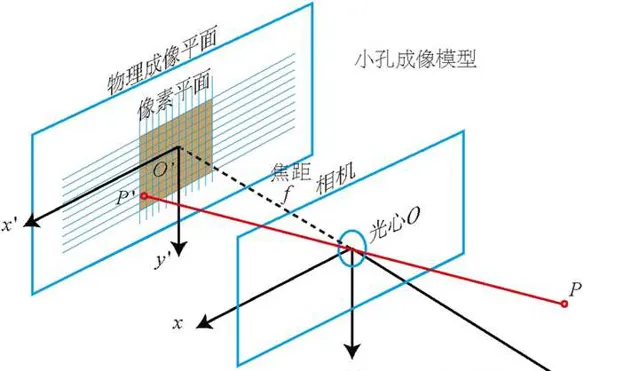
在数学上,针孔相机模型可以表述为:
\left[ \begin{matrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \frac{x}{z} \\ \frac{y}{z} \\ 1\\ \end{matrix} \right] = \left[ \begin{matrix} u \\ v \\ 1\\ \end{matrix} \right] \tag{2-1}
其中 f 为相机的焦距, c 为相机的光芯。 x,y,z 为点在三维相机坐标系下的坐标, u,v 为点在像二维素平面内的像素坐标。那么如果存在四维相机的,它的针孔相机模型就应该是:
\left[ \begin{matrix} f_0 & 0 & 0 & c_0 \\ 0 & f_1 & 0 & c_1 \\ 0 & 0 & f_2 & c_2 \\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \left[ \begin{matrix} \frac{p_0}{p_3} \\ \frac{p_1}{p_3} \\ \frac{p_2}{p_3} \\ 1\\ \end{matrix} \right] = \left[ \begin{matrix} u \\ v \\ w \\ 1\\ \end{matrix} \right] \tag{2-2}
这里 p_0, p_1, p_2, p_3 来表示点在各个轴下的坐标,u,v,w 表示像素坐标。这里我们很快注意到,像素平面是三维的,而人的视网膜是二维的。如果我们直接将三维的像素信息,都往 w = 0 的平面上叠加,从而得到一个二维图像。那么这个图像将是「重叠」的,将是文中所说的「透视」,将不再有 无限细节 。因此,对于地球文明的人类为何能借助二维的视网膜感受到四维世界的图像,这里给出一种解释:
地球文明原来是一个四维空间中的文明,在和边缘文明的战争中主动或被动地接受了降维打击。地球文明将自己压缩至三维空间下生存。但地球上人类仍然保留着第四个维度上的厚度(可能是一个较小的值,比如0.1mm)。因此地球人眼球是一个四维椭球,内部有一个三维的视网体,能够感知三维像素信息。由于我们生活的三维世界的光线没有第四个维度的分量,因此只有当人类进入四维碎块时,才会第一次感受到四维视觉。因此,针孔相机模型(2-2)的「升维」完成。在C++实现时,直接将相机模型封装为带维度参数的类,见camera.h。为验证实现的正确性,将虚拟世界 降维打击 至二维,在视野中防止四个二维的圆形,用线性相机拍摄可得一维图像:

再将虚拟世界 升维 至四维,在视野中放置一个四维球体和一个四维超立方体框架,用四维相机拍摄可得三维图像:

四维空间的相机所拍摄的照片,分辨率是三维的。遗憾地是作为三维世界的生物,我们的显示器都是二维的,因此我只能把第三个维度放在时间轴上。本文使用gif格式的图片来展示四维相机所拍摄的照片。
可以看到四维的球体在三维世界的投影是一连串大小均匀变化的三维球体,而且我们 不能看到球体内部结构 。而四维的超立方体,其实是两个三维立方体,然后把它们各自8个顶点连接。正如三维世界的立方体是两个正方形,然后把它们各自4个顶点连接。
四维刚体运动学
三维欧氏空间的大部分向量运算,如向量加法、内积等,都能通过直接增加向量维度来扩展至四维。三维向量叉积(Cross Product)无法直接扩展,却又是刚体运动学中非常重要的一种运算。比如速度与半径的叉积就是角速度。此外,刚体的旋转变换(Rotation Transformation)在三维空间下有多种参数化方法,对于正交矩阵的参数化方法,可以简单地扩充至四维,但是四元数(Quaternion)*、轴角法(Axis-angle)等更精简的参数化方式却无法扩展。
按照维基百科对四维旋转的描述可以发现,向量叉积和轴角法的不适用源自于同一个问题:
在四维空间下,一个二维平面的正交补空间(Orthorgonal Complement Space)是二维的。即一个二维平面有无数个不平行的单位法向量。再究其本质,旋转或者角速度这样的物理量,只能在三维空间下与单一向量保持映射关系。在高于三维的空间中,借用Clifford代数 [2] 的概念,表示为双向量(Bivector)。因此,本文使用四维正交矩阵来描述刚体的旋转。而使用「旋转平面-旋转角」的参数化方式来生成一些基础的旋转。
\huge R = (I - 2vv^\top)(I - 2uu^\top) \tag{3-1}
其中 R 为绕平面 A 旋转 \theta 弧度的旋转矩阵,向量 u,v 为平面 A 内,夹角互成 \frac{\theta}{2} 的两个单位向量 [3] 。公式(3-1)的另一种解释是:两个反射变换(Householder Transformation)构成一个旋转变换。
* 其实四元数能扩展到四维旋转。但是相比之下双向量(Bivector)能应对更高维的旋转。
四维视角下的三维封闭容器
在完成了针孔相机模型和刚体运动学的「升维」后,便可以利用这两个规则解答一个问题: 在四维视角下,观察者为何能够在不破坏容器的情况下得到三维封闭容器的内部信息 。我们可以在四维空间中建立一些简单的几何形状,或者导入一些常见的三维模型。通过刚体变换改变这些对象的姿态后,再用四维的相机拍摄下对象的「照片」。
首先把一只小黄鸭放入一个开口的容器:

盖上盖子后,理所当然地,观察者无法观察到容器中的任何信息:

下面使用分辨率为640x480x64的四维相机进行拍摄。


需要注意的是,虽然四维照片是一个动图,但所有帧都是在同一时刻被记录下的。所以整个图像没有任何对象在运动。为了模拟真实的四维视觉,三维世界的读者可以记忆下动图的每帧内容,然后闭上眼睛,让每一帧在大脑中同时出现,或铺展开来。
可以看到四维视角下的三维物体均薄如一张平面(其实是我在程序中给定了一个非常小的厚度,否则光线追踪算法无法判断光线与物体相交)。但是物体的每一个断层都清晰可见。由于小黄鸭的内部是均匀材料,所以相比书中蓝色空间号的四维视角下的图像,信息更少。
小结
通过简单地仿真可以看到,三维封闭容器的内部信息在四维视角下暴露无遗。上文的场景,相机第三轴的分辨率仅为64像素,且模型对象材料单一。如果能突破这两个限制,则可以渲染出书中所说的 无限细节 。本文所使用的代码放在github上,欢迎有兴趣的读者深入讨论!
一些书中场景的补充:
击落水滴

—— 褚岩
魔戒(墓地)
[开发中……]
这是人类第一次近距离看到四维物体,与高维空间感相似,他们感受到了被称为高维质感的宏伟。「魔戒」是全封闭的,看不到内部,但能感觉到一种巨大的纵深感和包容性。在来自三维世界的眼光中,所看到的「魔戒」不是一个「魔戒」,而是无数个「魔戒」的叠加,这种四维质感摄人心魄,是真正的纳须弥于芥子的境界。参考
- ^ Ray Tracing in One Weekend https://raytracing.github.io
- ^ Clifford Algebra, wikipedia https://en.wikipedia.org/wiki/Clifford_algebra
- ^ Two Reflections is a Rotation https://www.youtube.com/watch?v=Hy2gbdbrJZ8&list=PLpzmRsG7u_gqaTo_vEseQ7U8KFvtiJY4K&index=5











