以下讨论比较trivial,给与我同是初学者的人来看看。
定义范畴等价的动机在于,如何更好地刻画两个范畴是「一样的」这个概念。范畴同构太强了,需要函子 F:\mathcal{C}\to \mathcal{D} 与 G:\mathcal{D}\to \mathcal{C} 的复合必须分别 等于 \mathcal{C} 与 \mathcal{D} 上的恒等函子,而范畴等价只需要分别 自然同构于 \mathcal{C} 与 \mathcal{D} 上的恒等函子。
这个条件放宽会带来什么差异呢?可以证明, F:\mathcal{C}\to\mathcal{D} 是范畴同构当且仅当:
- full: 对任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是满射
- faithful: 对任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是单射
- surjective: 对任意 D\in \text{Obj}(\mathcal{D}) ,存在 C\in \text{Obj}(\mathcal{C}) 使得 F(C) 等于 D
- injective: 如果 A,B\in \text{Obj}(\mathcal{C}) 使得 F(A)=F(B) ,则 A=B
而 F:\mathcal{C}\to\mathcal{D} 是范畴等价当且仅当:
- full: 对任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是满射
- faithful: 对任意 A,B\in \text{Obj}(\mathcal{C}) , \text{Hom}_\mathcal{C}(A,B)\to \text{Hom}_\mathcal{D}(FA,FB) 是单射
- essentially surjective: 对任意 D\in \text{Obj}(\mathcal{D}) ,存在 C\in \text{Obj}(\mathcal{C}) 使得 F(C) 同构于 D
由此我们可以看到,范畴同构与范畴等价的区别完全在于后面对object的限制条件:范畴同构需要both surjective and injective,而范畴等价仅仅需要essentially surjective就好了。
这就告诉我们,假如说我们有范畴同构(当然同时也是范畴等价),如下图所示:
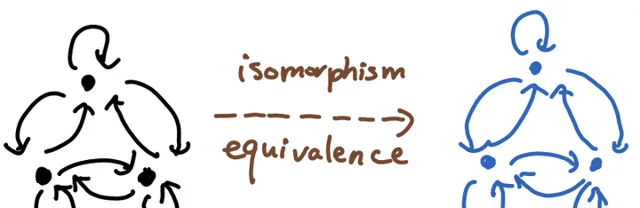
我们只需要在右面的范畴(蓝色)再添加一些object(下图橙色点),使得新的object同构于某些旧的object,就可使得这两个范畴不再同构,但仍然保持范畴等价,因为刚才添加新的object的这个操作仍然保持essentially surjective

换句话说,我们只需要同构地copy许多份object,就会破坏范畴同构但仍然保持范畴等价。
这也解释了为什么相比范畴同构,我们还需要范畴等价:因为我们希望允许随意地copy许多份object,反正copy过后本质上结构没有发生变化。
文小刚老师居然点赞了,受宠若惊。











