以高中生极其不严谨水平,瞎写一篇。这篇文章去年五月写的,原本为了「研究性学习」,但后来也没用上。留在草稿箱里也不是事,不如发表,供读者参考。班门弄斧,望不吝指正。
一、一个问题
都要从一个问题说起:
如图,距离太阳(S)距离d的P点处有一颗小行星,小行星无初速(对S),受到太阳引力缓缓坠向太阳,坠落时间为T。E为地球的轨道,轨道半径为R。太阳的质量是M,万有引力常量为G,求P由静止开始坠向太阳所用的时间。
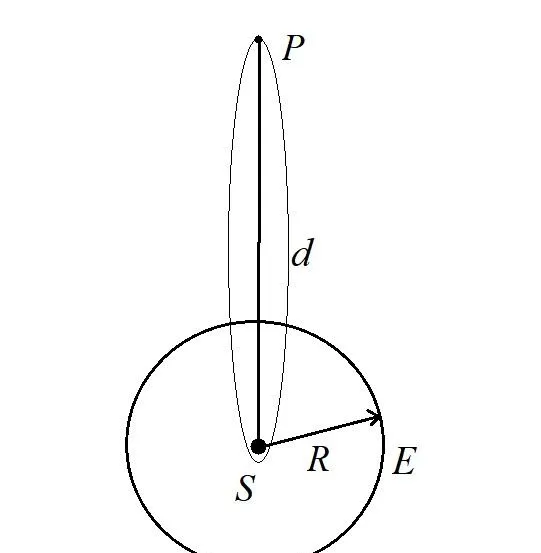
乍一看,随着时间的增加,物体的加速度越来越快,最后趋于无穷。位移与时间不是传统高中的一次或者二次关系,很难用传统手段解决。
本题的一种解法很巧妙,用到了Kepler第三定律:
注意到,P的轨迹其实可以视作短轴长\longrightarrow 0 的椭圆轨道\\ 于是由Kepler第三定律,\\ \frac{(\frac{d}{2})^3}{(2T)^2}=\frac{GM}{4\pi^2} \\解出\\ T=\frac{\pi }{2}\frac{d^\frac 3 2}{\sqrt{2GM}}\ \ \ (1)
这固然是十分优美而天才的解法,可是如果把题目变换一下,又会怎么样呢?
比如,我们要求 这颗小行星半途时通过的时间(P1-1) ,那么就要用到椭圆面积的极限,而这很可能没有一个很好的解法。因此,我们就需要回过头来,用一种较为普遍的方法解决原问题。
介于此,我们不得不将目光投向高等领域。发现加速度是位移的二阶导,而且它们满足 a \propto -\frac 1 {x^2} ,于是有微分方程: \frac{\mathrm {d^2} x}{\mathrm d t^2}=-\frac k {x^2} 。
这里分享一种原创的解法:
注意到a\ \mathrm d t=\mathrm d v\ ; v\ \mathrm d t={\mathrm d x}\\ 相比得\frac v a = \frac{\mathrm d x}{\mathrm d v}\ \ \ (2),带入a=-\frac{k}{x^2}, 这里k=GM为常数\\ \frac v {-\frac{k}{x^2}} = \frac{\mathrm d x}{\mathrm d v}\\ v\ \mathrm{d}v=-\frac{k\ \mathrm{d}x}{x^2}\\
这个处理技巧后面仍会进一步研究,现在变成了一个关于x,v的分离了变量的微分方程,两边同时积分,
\int v\ \mathrm d v=\int-\frac{k}{x^2}\ \mathrm{d} x \Longrightarrow \frac 1 2 v^2=\frac k x+C
带入初始条件 v=0,x=x_0 (为避免与积分号 \mathrm d 混淆,下用 x_0 代替原题目中 d )得
\frac 1 2 v^2=\frac k x - \frac k {x_0} \Longrightarrow \frac {\mathrm d x}{\mathrm d t}=\sqrt{2k(\frac 1 x - \frac 1 {x_0})}
进一步分离变量,整理得 \sqrt{\frac{x_0}{2k}}\frac{\mathrm d x}{\sqrt{\frac {x_0} x -1}}=\mathrm d t ,积分得
\frac{\sqrt{x_0}}{\sqrt{2k}}\int \frac{\mathrm d x}{\sqrt{\frac{x_0} x -1}}=\int \mathrm d t
接下来我们算一下 \int \frac{\mathrm d x}{\sqrt{\frac{x_0} x -1}} 这个不定积分,注意到可以三角换元
令x=x_0\cos^2\theta,\ \mathrm d x=2 x_0 \sin \theta \cos \theta \ \mathrm d \theta, \theta=\cos^{-1}\frac{x}{x_0}\\ \frac{\mathrm d x}{\sqrt{\frac{x_0} x -1}}=\frac{2 x_0 \sin \theta \cos \theta \ \mathrm d \theta}{\sqrt{\frac 1 {\cos^2\theta}-1}}=-2x_0\cos^2\theta\ \mathrm d \theta\\ 于是\\ \int \frac{\mathrm d x}{\sqrt{\frac{x_0} x -1}}=2x_0\int \cos^2 \theta\ \mathrm d \theta=x_0(\theta +\frac 1 2 \sin2\theta+C)\\ =x_0\arccos \frac x {x_0}+\frac{x}{x_0}\sqrt{x_0^2-x^2}+C_1
代入初始条件 t=0, x=x_0 ,得出
t=\sqrt{\frac{x_0}{2k}}(x_0\arccos \frac x {x_0}+\frac{x}{x_0}\sqrt{x_0^2-x^2})\ \ \ (3)
我们发现,如果令x=0,
t=\sqrt{\frac{x_0}{2k}}(x_0\arccos 0)=\frac \pi {2}\frac {x_0^{3/2}}{\sqrt{2k}}
即为式(1),与原题中解法得数一致。
回到P(1-1),只需令x=1/2x_0
t_1=\sqrt{\frac{x_0}{2k}}(x_0\arccos \frac 1 2+\frac 1 2\sqrt{x_0^2-\frac 1 4x_0^2})=\sqrt{\frac{x_0}{2k}} (\frac \pi 3+\frac{\sqrt{3}} 4)x_0=(\frac \pi {3}+\frac {\sqrt 3}{4})\frac{x_0^{3/2}}{\sqrt {2k}} \approx 1.48021 \frac{x_0^{3/2}}{\sqrt {2k}}
为从最远端到中途的所需时间。于是可以算出中途到近端时间:
t_2=(\frac \pi 6-\frac{\sqrt 3}{4}) \frac{x_0^{3/2}}{\sqrt{2k}} \approx 0.09059 \frac{x_0^{3/2}}{\sqrt{2k}}
我们得到的结果并不是一堆带着arccos函数的怪物,却是一个由 \pi 、 \sqrt{} 和自然数构成的奇妙常数!也算是一个令人惊讶的发现。
二、 不同的一维a-x关系
有了上面的推导作为先例,我们可以将a-x关系改一改,玩一玩。
对一般的 a=a(x) ,关系式又是什么呢?
本质上是要解微分方程 \frac{\mathrm{d}^2x}{\mathrm{d}t^2}=a(x) ,类似地推导可知
\frac 1 2 v^2=\int a(x)\ \mathrm d x\ +C \\ \implies \frac{\mathrm d x}{\mathrm d t}=\sqrt{2\int a(x)\ \mathrm d x\ +C}\\ \implies \int \frac{\mathrm d x}{\sqrt{2\int a(x)\ \mathrm d x\ +C_1}}=\int \mathrm dt=t+C_2 \ \ \ (2)
为一般解。
比如,考察 a(x)=\tau x ,则有
t=\int \frac{\mathrm d x}{\sqrt{2\int a(x)\ \mathrm d x\ +C_1}}+C_2=\int \frac{\mathrm d x}{\sqrt{\tau x^2\ +C_1}}+C_2 \ \ \ (3)\\ t_{1}=\int_{x_0}^{x_1} \frac{\mathrm d x}{\sqrt{\tau x^2\ +C_1}}+C_2 \ \ \ (4)
C_1,C_2 是常数,定义如下: v_0 是 t=0 初速度, x_0 是初始位置, C_1=v_0^2 -\tau x_0^2 , C_2=0 。 t_1 至从 x_0 到 x_1 的距离所用时长。
可以用到积分公式
\int \frac{\mathrm d x}{\sqrt{\tau x^2+C_1}}= \begin{cases} \tanh^{-1}(\frac{\sqrt \tau x}{\sqrt{\tau x^2+C_1}})+C_3,& \mbox{if }C_1\geq 0 \\ \frac{1}{\sqrt {2\tau}}{\ln\frac{\sqrt{\tau}x+\sqrt{\tau x^2+C_1}}{\sqrt{\tau x^2+C_1}-\sqrt \tau x}}+C_3', & \mbox{if }C_1< 0 \end{cases} .
这里 C_1 的正负取决于我们给的条件。
暂时先写这么多吧。











