拉格朗日量 (Lagrangians,简称为拉氏量)是一种数学表达式,它包含了一个物理系统中几乎所有我们关注的信息。拉氏量通常具有 对称性 ,这意味着当我们以某种特定方式转动或移动它们时,它们并不会发生改变。对称性和拉氏量非常重要,因为我们可以利用它们构造 守恒量 。
守恒量是在整个物理系统演化过程中保持不变的可观测物理量。
物理学家喜欢寻找守恒量,因为它们不仅具有深刻的哲学意义,还在解方程过程中非常有用。当你知道有些量保持不变时,用它们可以简化方程的求解。
旋转 这样 「平滑」的对称性是 连续对称性 。 诺特定理 表明,对于每一个连续对称性,我们都可以构造一个守恒量。例如,如果一个系统具有旋转对称性,我们就可以得到角动量守恒 。
更令人惊讶的是,诺特定理可以证明能量守恒是时间平移对称性的结果,时间平移不变性 意味着拉氏量本身 不显含时间 。
换句话说,如果物理系统所处的背景不随时间改变,那么该系统的总能量将不随时间改变。

对称性 的概念在力学、经典和现代物理学中随处可见。例如,在量子物理学中,量子力学系统的对称性可以与量子角动量守恒对应。在电子理论中,电子的电荷和自旋守恒 源于电子所遵循的对称性。
用数学如何详细描述对称性起的作用?首先,需要解释 最小作用量原理 ,以及如果我们知道了拉氏量,我们如何用它来计算场的行为。
作用量和拉氏量
假设有一个粒子或场,在两个预先确定的时间点 t1 和 t2 之间演化。如果它是一个粒子,我们可以通过绘制一条在空间中延伸的路径来描绘粒子的演化过程,从时间 t1 开始,到时间 t2 结束。如果它是一个场,我们可以想象一个热力图 随着时间慢慢演化。
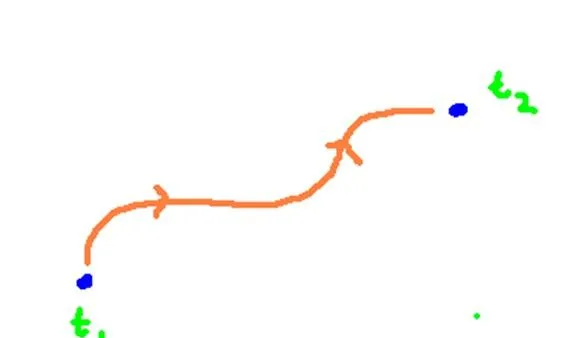
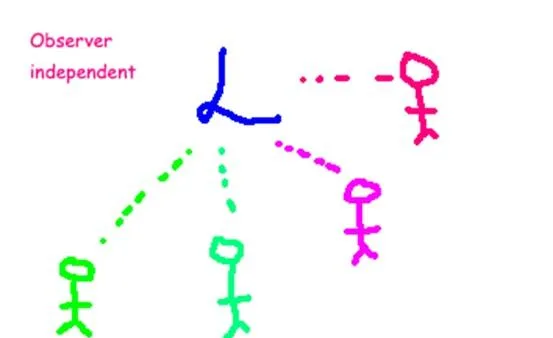
通过这些粒子和场的行为,我们能知道些什么?我们怎么才能知道粒子将走什么路径?在物理学中,我们从一个可以描述物理系统的模型开始,其中典型的一种是拉氏量。拉氏量是一个数学量,它通常写成 动能和势能之差 ,拉氏量在任何时间点都可以给出一个具体的数。我们之所以喜欢用拉氏量是因为它 独立于观察者 ,不随参考系的改变而改变。
观察者是正立的还是倒立的,或者以接近光速的速度移动,这些都不重要。通常,物理量的数值会因坐标选择的不同而不同;然而,拉氏量不随坐标的选择而改变,无论对于哪个观测者,它的取值都是一样的。和参考系 无关的这种性质是非常有用的,因为它让我们可以进行清清楚楚的计算。
为了理解到底发生了什么,我们需要构造一个称为 作用量(action) 的量。例如,如果已知一个拉氏量,我们可以计算拉氏量在两个时间点之间的 积分 :

积分意味着将拉氏量在多个时间点上的值进行相加。从t1 到t2之间的总积分被称为作用量。它通常用大写字母 S 表示。拉氏量前面的竖直曲线 ∫ 表示积分。
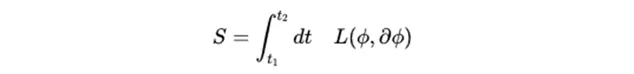
上面的表达式是作用量的数学定义。拉氏量通常是位置和位置的 一阶导数 的函数 。希腊字母 φ 表示粒子在空间中的位置;第二项 ∂φ 是粒子位置的一阶导数,表示粒子位置随时间的 变化率 。
拉氏量 在几何上看起来是怎么样的?我们可以用一些插图来说明,通过这些插图可以了解关于它的一般概念。如果拉氏量只包含自由空间中的动能,对于不同于直线的路径,往往会得到更大的作用量。该图显示了粒子在时间t1和t2之间采取不同路径对应的作用量大小。正如您所看到的, 最复杂的路径作用量最大 。作用量最小的路径就是直线路径。

如何得出物理规律?
在我们眼中,拉氏量是数学对象,我们只把 作用量 看作是物理的。这有一个哲学上的原因。结果表明,不同的拉氏量可以产生相同的作用量。所以,在某些情况下,存在两个拉氏量,但只有一个作用量的情况。这意味着我们可以通过两个不同的拉氏量,得出相同的物理定律 。
为什么会这样?原因是,当我们对某些被称为「 全微分 」(total derivative)的数学表达式进行积分时,积分结果是零。
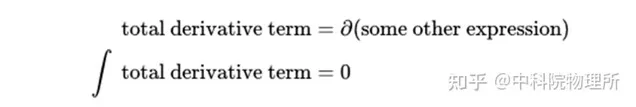
在下面的公式中,我们有一个作用量,被写成一个特定的拉氏量和一个全微分项。但是,我们可以把积分拆分成两个不同的部分。一旦我们把它分开,我们就消掉了全微分项,因为当我们积分时它变成了零。
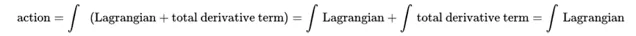
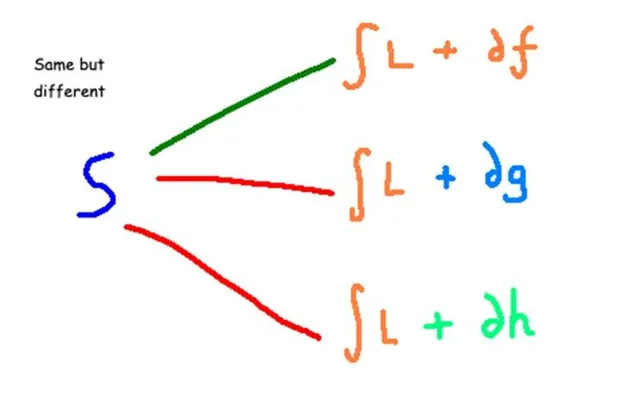
这是一件令人兴奋的事情!这意味着,存在两个不同的拉氏量,在一个不那么严格的限制下,可以认为它们是「等价」的。我们不需要让它们完全等价就能得出相同的物理现象。如果拉氏量仅在「全微分」项上存在差异,则它们可以被看作是相互等价的。例如,在下图中,函数 f 、 g 和 h 都与全微分项有关,它们三个产生相同的作用量。(我已经用不同的颜色写出了这三个函数来表达这个观点。)
数学上,我们可以用下面的表达式来表达拉氏量之间「等价」,尽管它们之间相差一个全微分项。在下面的表达式中,函数 f 是 可微函数 。
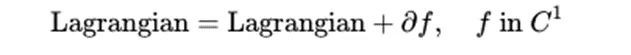
如果对函数可以使用「变化率」的概念,那么这个函数就是可微的。如果函数值在某些地方发生跳跃、出现尖锐的拐点或没有 良定义 ,那么就有可能不能使用「变化率」的概念,这种情况下,只有许多严格的数学条件被满足时,「变化率」的概念才变得可以接受。所有可微函数的集合为C¹。关于微分和积分 等运算是否具有良定义的研究称为数学分析,是一个令人着迷的研究领域。
欧拉-拉格朗日公式
「最小作用量原理 」告诉我们,场或粒子的行为正是使作用量取 极小值 的行为。所以如果我们知道这个作用量,我们可以通过一些数学运算,求出使这个作用量取极小值时场的行为。有一个被称为 变分法 的数学分支,研究的是「函数的变化率」。(译者注:变分法告诉我们,场或粒子的行为可以用欧拉-拉格朗日方程导出。)
粒子版的欧拉-拉格朗日方程如下所示。方程左边,我们首先取拉氏量对速度的偏导数 ,然后继续对其求时间的导数。方程右边,我们对拉氏量在空间中进行求导。然后让方程的左边等于右边,就可以得到一个令作用量取最小值的路径。
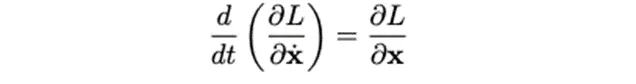
场论版的欧拉-拉格朗日方程 和粒子版的很相似,方程如下所示:
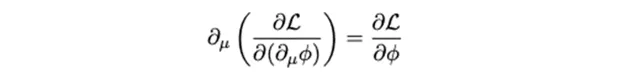
它可以给出场在时空中的 演化方式 。
以下为译者注:
守恒量
前面我们介绍可以用对称性导出守恒量,接下来我们将介绍如何做到这一点。诺特定理告诉我们,每个对称性对应一个守恒量。
如果物理系统具有时间平移不变性,也就是说拉氏量不显含时间,那么可以得到表达式:
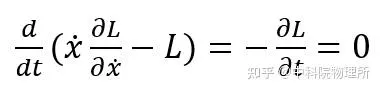
等式左侧的括号里就是能量(哈密顿量 ),它随时间的导数是零恰恰表明它不随时间改变。
如果物理系统具有空间平移不变性,也就是说拉氏量不显含空间坐标,那么可以得到表达式:
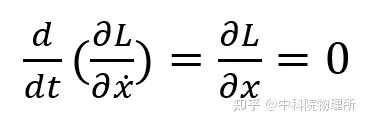
等式左侧括号内正是(共轭)动量,它不随时间改变,这就是 动量守恒 。
作者:Afiq Hatta
翻译:Nothing
审校:Zhenni
原文链接:
https://www. cantorsparadise.com/noe thers-theorem-and-the-principle-of-least-action-c84b789c51b6











