题主所提到与运动方向同向的光速问题还真就不能直接回答,咱们必须换一个角度,先研究一下光与运动方向垂直时的情况。随着一步一步递推下来,水到渠成,问题就迎刃而解了。(放心,我只用了一点简单的代数,上过中学的人都应该看得懂)
那么先想象这样一个场景:
【思想实验一】 [1]
观察者B站在地面上。头顶有一艘飞船,以速度v [2] ,在平行于地面的方向上,匀速向右飞行。飞船上安装了一台光子钟,仪器的下端有发射器向上发射光子,仪器上端则装有镜面,光子被镜面反射向下,回到下端初始位置时由探测器接收。此钟可测出光子从发射到返回所经过的时长。宇航员A在飞船上记录光子钟的读数。对他而言,光子是在垂直的方向上做往返运动,光子的发射与接收发生在 同一位置 。
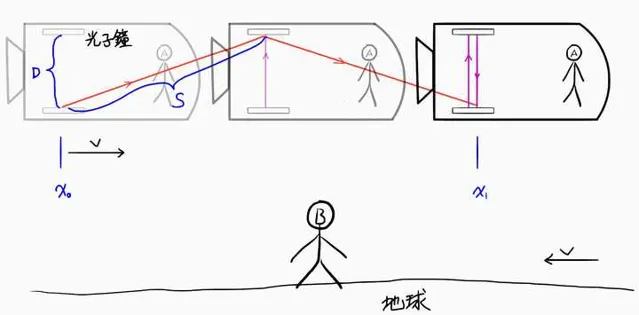
由于飞船相对于地面有一个水平方向的速度v,那么对地面的观察者B而言(假定他也能看到飞船中的一切),飞船上光子钟里光子所走的路线则是斜上斜下的「人」字形,光子的发射和接收发生在水平方向一左一右 两个不同的位置 上 。
设光子钟上下两端的间距为D,观察者A所观测到的光子的往返路程为2D,时长为τ;地面观察者B所观测的光子上行和下行路径长度同为S,光子往返的总路程为2S,时长为t。
速度= 距离/时间
两个观察者都可以根据自己测得的时间和距离算出光速,那么 光速不变 即意味着
\frac{2D}{\tau} = \frac{2S}{t} = c
即 * 距离与时长的比值不变 *!
飞船相对于地面的速度 v 是明确的,那么从光子的发射到接收,飞船在水平方向上所通过的距离对地面观察者B而言就等于 vt。令 2L=vt ,我们即可得出如下图所示的两个全等直角三角形。
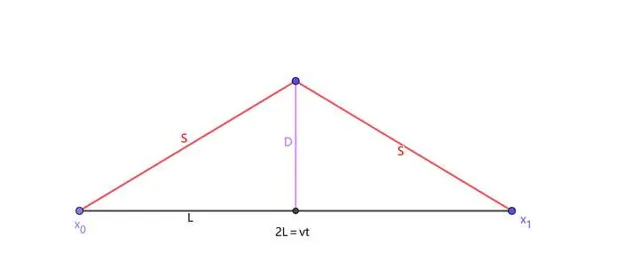
根据毕达哥拉斯定理(勾股定理), S^2 = D^2 + L^2 ,若将A、B二人所记录的时长、距离以及不变的光速c代入,即可得:
\begin{align} S^2 =& D^2 +L^2\\ (ct)^2 =& (c\tau)^2 + (vt)^2\\ c^2t^2 =& c^2\tau^2+v^2t^2\\ (c^2 -v^2)t^2 =& c^2\tau^2\\ t^2 =& \frac{c^2}{c^2-v^2}\tau^2\\ \color{red}{t} = &\frac{1}{\sqrt{1-(v/c)^2}}\color{violet}{\tau} \end{align}
τ 前面的这个系数 \frac{1}{\sqrt{1 - v^2/c^2}} 就叫做 洛伦兹因子 ,记作 γ 。也就是说,B所记录的光子的往返时长 t 跟A所记录的时长 τ 是不一样的。如果你把A、B两者的相对速度 v 代入,假令 v = 0.5c,会发现 γ = 1.1547 > 1。 \because v <c ,\therefore \gamma > 1 。
同样的两个事件的间隔(光子的发射和接收)在B参照系里的耗时比A参照系里的长,或者反过来说,A的时钟比B的时钟走得慢——这就是「 时间膨胀 」。
于是你要问了。既然速度 v 是相对的,对地球上的 B 而言,飞船上的时钟变慢了,对飞船上的A而言地球上的时钟是不是也变慢了呢?—— 确实如此 。所以我们必须回过头来留意一下前文中加了黑体的条件:对飞船上的 A 而言,两个事件是发生在同一位置的。因此,他所测得的时间就叫作 原时 (或曰固有时间 proper time)。而对地面上的 B 而言,两事件发生在不同位置,那么他所测得的时间就是 γτ 。当然,如果把实验颠倒过来,把光子钟放在地面上,地面上测得的时间就成了原时了。
速度总是相对的, A 相对于 B 的速度是 v, 那么 B 相对于 A 的速度也必然是 v,于是问题来了。回看一下上图的三角形,光子的往返过程中,飞船相对于B向右横向移动了 2L 的距离。B观察到,光子钟收发点的水平位置从 x_0 移动到了 x_1 。既然 v_A = v_B ,那不就意味着 \frac{2L}{t} = v = \frac{?}{\tau} 嘛!对飞船上的A而言,地面相对于他自己是在向左移动。难道在光子往返的 τ 时间内,地面移动的距离竟然不是2L?没错! 将洛伦兹因子代入,
\begin{align} \frac{2L}{t} =& \frac{2L'}{\tau}\\ \frac{2L}{\gamma \tau} =& \frac{2L'}{\tau}\\ L' =& \frac{1}{\gamma}L \end{align}
对地面上的B而言, x_0 和 x_1 两个点(位置)是静止的,我们把相对于观察者静止的两点间的距离称作 原长度 (或曰固有长度 proper length),通常记作 L_0 。而相对两个点运动的观察者所测得的两点间的距离(如前面式子中的L')则是原长度的1/γ 倍(恒< 1)。也就是说,飞船里A所量得的水平方向上相对其运动的长度(比如飞船的飞行路程)是短于地面上B所量得的静止长度的,我们把这个现象就叫做「 长度收缩 」。
还有一个问题,那就是与运动方向垂直的长度。就比方说这个光子钟的上下两端的间距,会不会对A、B而言也不一样呢?倘若D_A \neq D_B ,以上的一连串推导就都不成立了。看下图:
【思想实验二】
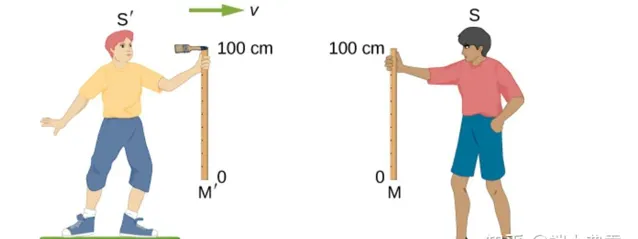
两男孩(S' 和 S)各拿一把静止时长度为1米的直尺,垂直举起。男孩S'的尺子上端固定了一个蘸了墨的毛刷。S在地面站定,而S'以极高的速度 v 向着与S稍稍错开一点的方向滑行过来。当两者擦肩而过时,两人尺子的下端距地高度相同,尺间的距离也是毛刷能够得到的。如果事后S检查自己的尺子M,发现上端下面一点有一道墨迹,就说明,S'的尺子M' 比自己尺子M短。然而速度是相对的。对S'而言,自己才是静止的,是 S 以速度v迎面而来,如果以高速 v 运动会使竖直方向的尺子变短的化,在两人交会的一刹那,S'会看到自己尺子上的毛刷在对方尺头上空划过。事后检查,S的M尺上应该没有墨迹。毛刷在尺子上画出墨迹这件事怎么能既发生又不发生呢?这明显是个悖论。所以说,垂直于运动方向的两把尺子必定是等长的,即 D_A = D_B 。
Okay, 终于可以讨论「追光」的问题了。还是一开始设定的那个场景,只不过,这回飞船上的光子钟横过来装。让光子钟收发和反射两端的间距正好等于飞船的长度。如下图:
【思想实验三】
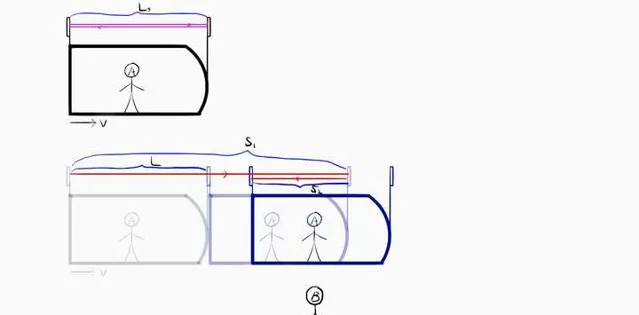
飞船上的A量得的飞船长度是 L_0 ,因为A相对于飞船的两端静止,所以这个长度就是原长度。又对A而言,光子的发射接收发生在同处,所以他测得的时长 τ 也就是原时。于是他的光路方程就是 2L_0 = c\tau 。(图示的上半部分)
地面上的B量得的飞船长度是L。他所观测到的光子的路径 S 由前进阶段的 S_1 和返回阶段的 S_2 两段组成。(图示下半部分)
我们需要先搞清楚 S_1、S_2 跟船体长度 L 的关系。先假定光子走完 S_1 所经过的时间为 t_1 , S_2 所对应的则为 t_2 。那么
S_1 = ct_1 = L + vt_1 \implies L = (c-v)t_1 ,进而知 \frac{S_1}{L} = \frac{c\cancel{t_1}}{(c-v)\cancel{t_1}} 。同理, S_2 = ct_2 = L - vt_2 \implies L = (c+v)t_2 \implies \frac{S_2}{L} =\frac{c}{c+v} 。于是 \frac{S}{2L}=\frac{S_1 +S_2}{2L} = \frac{c^2}{c^2-v^2} =\frac{1}{1-(v/c)^2} 。
又由于长度收缩, L = \frac{L_0}{\gamma} \implies S = \frac{S}{2L}\cdot \frac{2L_0}{\gamma}= \frac{1}{1-(v/c)^2}\cdot\sqrt{1-(v/c)^2}\cdot L_0 = \gamma \cdot 2L_0
也就是说,地面所观察到的光子路程是飞船上所观察到的γ倍。
又由于时间膨胀,地面观测到的光子往返时间 t = \gamma \tau 。
\frac{S}{t} = \frac{\cancel{ \gamma} \cdot 2L_0}{\cancel{\gamma} \tau} = c
——理解了没?
参考
- ^ 本文所举之「实验一」「实验二」,以及对「时间膨胀」「长度收缩」的解释均取材于Rice大学的Openstax教材【University Physics Volume III】 https://openstax.org/details/books/university-physics-volume-3
- ^ 本文所言的「速度」严格来讲,所指都是「速率」(speed),而非矢量的「速度」(velocity)。光速不变的速,指的就是speed。我之所以选用这种含混的说法,是因为我觉得汉语的「速率」一词太拗口。











