这道题看起来像是一道算法题,本质上却是披着猪皮的 信息论 问题。解答这道题并不是我的目的,我的目的是用信息论的思维来思考,达到触类旁通,一通百通。
用信息论去思考的另一个好处就是,信息论给了这类问题的一个边界,让我们在边界范围内思考问题。很难想象,70多年前的 香农 已经用严格的理论证明为这类问题设定了一个极限,任何想逾越这个极限去解决问题的人最后都会被证明是徒劳的。
这也是理论武装头脑的好处,当别人还在尝试是否有更优的解法时,你可以直接给出最优答案,用信息论降维打击。即使我可能暂时无法想出具体的方案,但我知道这类问题的一个理论极限在哪里,没有必要为超越极限做无用功。
所以,在解题之前我觉得有必要补充一下理论知识,让我们了解一下信息论中「 信息熵 」。
信息熵
1. 热力学中的熵
熵 的概念最早起源于物理学,用于度量一个热力学系统的无序程度,也就是系统混乱程序。
熵增定律 指出:
在一个孤立系统里,如果没有外力做功,其总混乱度(熵)会不断增大熵增定律让我们知道,如果将一杯热水和一杯凉水倒在一起,并且不对水杯中的水做功,这杯水的冷热分子最终一定呈最混乱的分布,也就是最终整体温度均匀分布,绝对不会出现冷热水分层的现象。
如果把宇宙当成一个孤立系统,那么宇宙一定是从有序变为无序混乱的状态,当宇宙的熵达到最大值时,宇宙中的其他有效能量已经全数转化为热能,所有物质温度达到热平衡。这种状态称为热寂。这样的宇宙中再也没有任何可以维持运动或是生命的能量存在。
2. 信息论中的熵
在信息论中,熵的概念和热力学中是类似的,描述的是「 信息的不确定程度 」。
所以信息中的不确定性类似于热力学中系统的混乱程度。
所以也就是说,信息的不确定程度越大,信息熵也就越大。那什么样的信息不确定程度大呢?
比如抛一枚硬币,如果我来猜正反的话,那么我基本只能靠瞎蒙,因为不确定程度很大,正反的概率都是0.5。对于抛一次硬币猜正反这类事件来说,它的不确定程度很大,信息熵也很大。
如果中国男足和巴西男足比赛,让我来猜胜负,那么我几乎可以断言,巴西队一定会赢。也就是巴西队和中国队胜负这个事件的不确定程度很小,信息熵也就很小。
如果比赛后巴西队真的赢了,那么这条信息的信息量几乎为零,因为这条信息几乎没有降低信息的不确定度。
上面提到了 信息熵、信息、信息量 ,它们之间的比较如下:
上面都只是定性的分析,香农把随机变量 X 的熵值 Η定义如下,其值域为{ x 1, ..., xn }
\mathrm{H} (X)=-\sum _{{i}}{{\mathrm {P}}(x_{i})\log _{b}{\mathrm {P}}(x_{i})}
b是 对数所使用的底。当 b = 2,熵的单位是 bit 。
P为 X 的概率质量函数(probability mass function),我们可以理解为事件xi 发生的概率。
公式看起来可怕,其实非常简单。
让我们用抛硬币来举例,「抛一次硬币是正面」这个随机变量X的 信息熵 为
\mathrm{H} (X)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1
也就是抛一次硬币是正面这个事件的信息熵只需要1 bit,也就是只需要用1位的二进制数就可以表示这个信息大小。
题目的简化版本
在我们学习了信息熵的知识以后,让我们再来看题目。原题其实略微复杂一些,先将题目简化一下。
1000桶水,其中一桶有毒,猪喝毒水后会在15分钟内死去,想用15分钟内找到这桶毒水,至少需要几头猪?上面这道题其实也是当年google的一道面试题,只不过面试题中的小白鼠在这里被替换成了猪。原题是多次试验问题,简化后的版本是单次试验,更容易看到这道题的本质。于是我们利用上面介绍的信息熵的知识来求解一下。
首先,」 1000桶水其中有一桶有毒 「这个随机变量X的 信息熵 为
\mathrm{H} (X)=-log _{2}\frac{1}{1000} =9.966
1只猪喝水以后的要么活着,要么死去,一共有两种状态,所以」1只猪喝完水以后的状态「这个随机变量Y的信息熵为
\mathrm{H} (Z)=-(\frac{1}{2}log _{2}\frac{1}{2} + \frac{1}{2}log _{2}\frac{1}{2}) = -log_{2}\frac{1}{2}=1
n只猪喝完水会有 2^n 种状态,即"n只猪喝完水以后的状态"这个随机变量Y的信息熵为
\mathrm{H} (Y)=-\sum _{{i=1}}^{2^n}{\frac{1}{2^n}}{\log _{2}{\frac{1}{2^n}}}=-\log _{2}{\frac{1}{2^n}}=n
所以,按照题目要求,如果至少需要n头猪能够找到这桶毒水,那么随机变量Y的信息熵必须要大于随机变量X的信息熵,也就是
H(Y) >= H(X) ,也就是 n >= 9.966,即 n = 10
当我们用信息熵算出来了n的最小值以后,我们就可以坚信,理论上n=10一定是最优解,任何想方设法想找到小于10的值都是徒劳的。
其实,上面的信息熵计算的简化版本可以写成如下更好理解的形式
2^n \ge 1000
同样可以解得 n = 10 ,虽然形式简单,但我们一定要记住它背后的原理是信息熵。
至于到底采用什么方案,这涉及到术的层面,即使我们暂时想不到,我们也会有努力的方向,并且知道努力的边界在哪里,不会做类似寻找永动机的事情。
下面我们来看下图具体的方案
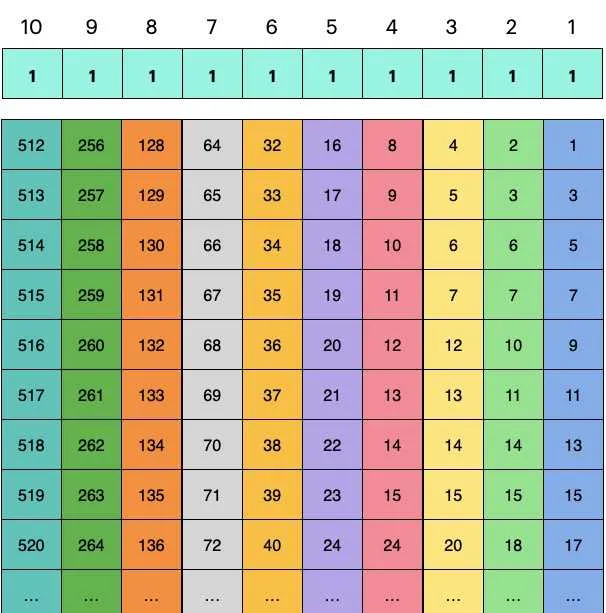
我们将1000桶水按照2进制编码,如上图第一行,需要10位二进制数。于是有
于是,我按照如下方案让猪进行喝水,如上图所示:
如果15分钟后1,3,5号猪被毒死,那么对应的二进制编码就是00000 10101b,也就是21号水桶有毒。更一般的,猪死的任何一种排列方式都对应了二进制的唯一编码。
这里为什么采用二进制的编码方式?
首先,我们要理解为什么计算机内部运算都采用二进制的方式,这是因为开关电路在计算机中实现起来非常简单,而开关两种状态正好对应了二进制的0和1。老式的计算机都是用继电器的开关实现的,而现代计算机也是利用逻辑电路的通断实现高低电压来表示0和1。所以计算机内部的运算其实都是将其转化为二进制再进行运算的。
而猪的生死正好对应了计算机中的开关电路,所以我们这里采用二进制进行编码。
而原题目多次试验的情况就不能采用二进制编码了。
原题目
1000桶水,其中一桶有毒,猪喝毒水后会在15分钟内死去,想用一个小时找到这桶毒水,至少需要几头猪?有了前面简化的版本的理解,我们容易得知
」 1000桶水其中有一桶有毒 「这个随机变量X的 信息熵 为
\mathrm{H} (X)=-log _{2}\frac{1}{1000} =9.966
而对于猪的状态就不太一样了,我们可以想象一下,一只猪在一个小时内会有几种状态?
- 在第0分钟的时候喝了一桶水以后,第15分钟死去。
- 第15分钟依然活着,喝了一桶水以后,第30分钟死去。
- 第30分钟依然活着,喝了一桶水以后,第45分钟死去。
- 第45分钟依然活着,喝了一桶水以后,第60分钟死去。
- 第45分钟依然活着,喝了一桶水以后,第60分钟依然活着。
可见,1只猪1个小时以后会有5种状态,所以」1只猪1个小时后的状态「这个随机变量Z的信息熵为
\mathrm{H} (Z)=-( 5 \times \frac{1}{5}log _{2}\frac{1}{5} ) = log_{2}5=2.3219
n只猪1个小时后会有 5^n 种状态,即"n只猪1个小时以后的状态"这个随机变量Y的信息熵为
\mathrm{H} (Y)=-\sum _{{i=1}}^{5^n}{\frac{1}{5^n}}{\log _{2}{\frac{1}{5^n}}}=-\log _{2}{\frac{1}{5^n}}=n \log_{2}{5}=2.3219n
所以,按照题目要求,如果至少需要n头猪能够找到这桶毒水,那么随机变量Y的信息熵必须要大于随机变量X的信息熵,也就是
H(Y) >= H(X) ,也就是 n >= 9.966 / 2.3219 = 4.292,即 n = 5
事实上, 对于 n = 5来说,不仅可以检测1000桶水,甚至检测3000桶水都是没有问题的。有兴趣的童鞋可以试着计算一下 。
到此,香农给了我们一个理论极限,但是具体的方案还是需要我们自己进行构造。 得出n=5是依靠我们的理论功底,而得出具体的方案就是我们的工程水平了。
根据前面简化版本的二进制编码方式的思路,我们是不是可以利用猪的5种状态构造一个5进制编码方式呢?如下图所示。

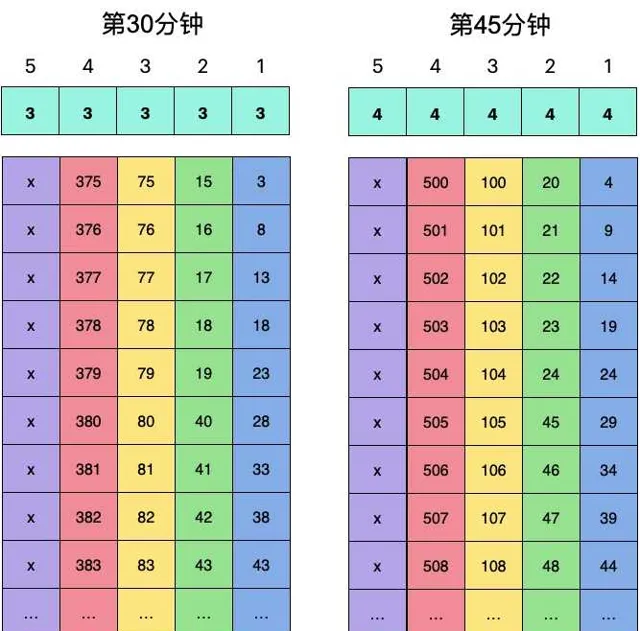
首先,将1000桶水按照5进制编码的方式排列,如上图所示,需要5位5进制数。
然后按照如下方案让猪进行喝水,如上图所示:
上面,猪的编号代表5进制编码数字所在的位数,1号猪代表最末位,5号猪代表最高位。而第几分钟死代表当前位数的权重,15分钟死表示权重是1,30分钟死表示权重是2,... ,60分钟死表示权重是4,60分钟依然活着表示权重是0。
如果1号猪第30分钟死了,2号猪第15分钟死了,3号猪第45分钟死了,4,5号都活到了最后。则毒水对应的5进制编码是
0 \times 5^4 + 0 \times 5^3 + 3 \times 5^2 + 1 \times 5^1 + 2\times5^0 = 82
也就是第82桶水有毒。
到此,这个问题从理论和工程上都给出了答案。信息熵让我们明确了工程上努力的方向并明确了那条不可逾越的鸿沟。
熵的拓展
前面提到了热力学中的「熵增定律」,其实在社会中「熵」也有重要的意义。
对于国家来说,如果闭关锁国,相当于一个孤立系统,就好比鸦片战争前的清政府,不与外界进行交流,也不进行贸易,也就相当于没有能量的交换,最终的结果必定是「熵增」,即越来越混乱,越来越没有效率。
所以必须保持对外开放的政策,与外界环境不间断的交换。比如:与世界各国进行贸易往来,招商引资,引进竞争,这些都是「负熵」的表现。
对于企业也是同理,必须引进「负熵」,比如现代化的管理方式,先进的技术等等。否则,企业内部不了解外部经济环境变化,也不了解终端用户,只能是最终能量耗尽而亡。
最后,希望本篇回答让你不仅了解了题目本身,更能知道信息论在解决类似问题时给出的指导意义,让我们具备自顶而下的思考方式,首先直击问题本质,将现实问题抽象成数学或者其他已知问题,然后用理论给出答案的边界,也明确的努力的方向和极限。接下来在工程上,保证在理论边界内去尝试,而不是一味地试图超越理论极限,做无用功。
而常人的做法往往是先尝试一种方案,发现应该还有优化空间,于是逐步优化,但是不知道努力的方向和边界。
所以往往要么在努力的过程中离边界值还有很大距离的时候就放弃了,要么就是试图突破边界而做无用功,要么努力了一大顿最后才发现极限的优化提升空间也只有2%,不得不更换方案。
这可能也是高手与常人的区别,希望本文能让大家了解这种自顶向下的思考方式。
2020-6-10号更新
看到评论中有很多对答案有疑问的,所以补充一下答疑,不一一回复了,谢谢。
1. 有的评论说,一只猪就够,每隔两秒钟喝一次。
请参见题目详情限制条件1
「1.一滴毒水足以导致一头猪的死亡。死亡时间为15分钟内不确定的某个时间点。」请仔细审题,不是恰好15分钟,而是最长15分钟。猪每隔两秒喝一次即使死了也是无法区分哪桶水有毒的。
仔细审题很重要啊!
2. 为什么题目中在计算猪的信息熵时采用了等概率?
很抱歉,这个我在解释的过程中忽略了。
首先要明确的是,猪在喝毒水的时候生和死的概率确实不一定是等概率的,这个是对的。
比如原题中,对于5号猪来说,因为它喝的水位于5进制的最高位上,所以它活的概率是 \frac{624}{1000} = 0.624 。
既然不是等概率,那正文中为什么采用等概率的方式呢?这是因为在计算信息熵的时候,我们考虑的是n只猪所能表达的最大信息熵。
数学上可以证明,当随机事件等概率发生的时候,信息熵是最大的 。
题目要求最少n只猪,意思就是在最差情况下用n只猪也能找到毒水。而最差的情况就是每只猪生死的概率是相等的。
所以我们用等概率的方式求出最大信息熵时最小的n,当n再小,最差情况下已经无法测出1000桶水了。
如果你觉得对你有帮助,请帮忙点赞,谢谢。











