比如用机器学习算法来预测学习者的长期记忆。机器学习是计算机科学下的一个分支,而长期记忆属于认知心理学下的一个热门研究方向。
可能有人会问,预测学习者长期记忆有啥用。我打个比方,在战争中,能够精确预测炮弹落点的一方,能够用更少的火炮,打击更多有价值的目标。在学习中,如果我们可以精确预测一个人所知的一切知识的记忆情况,我们就能制定相应的高效学习策略,用更少的时间记住更多的知识。
现在比较公认的、有实证研究支持的高效记忆方法叫做间隔重复(spaced repetition),这在心理学的学术界已经有很多研究了,比如下面这篇综述:

但是在传统心理学研究中,研究者通过设置实验能够收集到的数据非常有限,难以建立有关长期记忆的精确模型,更不用说设计高效的间隔重复算法了。不过现在已经有不少开源的大规模记忆数据集,比如:
有了这些数据,就可以对人类记忆进行建模。这里简单介绍一下我在这个领域的研究进展。
数据收集
数据是记忆算法的源头活水,没有数据,巧妇也难为无米之炊。收集合适、全面、精确的数据,将决定记忆算法的上限。
为了精准的刻画学习者的记忆情况,我们需要定义出记忆的基本行为。先让我们思考一下,一个记忆行为,包含哪些重要属性?
最基本的要素很容易想到:谁(行为主体)何时(时间)做了什么事(记忆)。对于记忆,我们又可以继续挖掘:记了什么(内容)、记得怎么样(反馈)、花了多久(成本)等等。
考虑到这些属性之后,我们便可用一个元组来记录一条记忆行为事件:
e:=(user,item,time,response,cost)
该事件记录了一个用户 user 对某条材料 item 在某个时刻 time 作出了某类反馈 response,付出了多少成本 cost。举例说明:
e:=(\textrm{小叶},\textrm{apple},\textrm{2022-04-01 12:00:01},\textrm{忘记},\textrm{5秒})
即:小叶在 2022 年 4 月 1 日 12 点 0 分 1 秒记忆了 apple 这个单词,反馈忘记,用时 5 秒。
有了基本的记忆行为事件的定义,我们在此基础上,抽取、计算更多感兴趣的信息。
比如,在间隔重复中,两次重复之间的时间间隔是一个重要的信息,利用上述记忆行为事件,我们可以将事件数据按照 user、item 分组,按 time 进行排序,然后将相邻两次事件的 time 相减,即可得到间隔。通常来说,为了省去这些计算步骤,可以直接将间隔记录在事件中。虽然造成了存储冗余,但能够节省计算资源。
除了时间间隔之外,反馈、间隔的历史序列也是一个重要的特征。比如「忘记、记得、记得、记得」、「1 天、3 天、 6 天、10 天」,这些信息能够较为完整地反映一个记忆行为的独立历史,也可以直接记录到记忆行为事件中:
e_{i} :=(user, item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , r_i)
DSR 模型
有了数据之后,该如何利用呢?其实我们想要知道的是记忆状态的种种属性,而我们目前收集的数据暂时不包括这些内容。因此,如何将记忆数据转换成记忆状态和状态之间的转移关系,是本节的目标。
记忆状态
DSR 模型的三个字母分别对应难度(difficulty)、稳定性(stability)和可提取性(retrievability)。让我们先从可提取性入手。可提取性反应了记忆在某时刻的回忆概率,但记忆行为事件已经是进行回忆后的结果。用概率论的语言来说,记忆行为是只有两种可能结果的单次随机试验,其成功概率等于可提取性。
因此,若要测得可提取性,最容易想到的方法就是对同一个记忆进行无数次独立实验,然后统计回忆成功的频率。但这种方法在实际上是不可行的。因为对记忆进行实验,将改变记忆的状态。我们无法作为一个观察者,在不对记忆造成影响的情况下对记忆进行测量。(注:以目前的脑科学水平,还无法在神经层面测量记忆的状态,因此这条路目前也用不了)
那么,我们就束手无策了么?目前有两种妥协的测量方式:(1)忽略记忆材料的差异:SuperMemo 和 Anki 都属于此类;(2)忽略学习者的差异:MaiMemo 属于此类。(注:其实现在已经考虑了,只是在我刚动笔写这段话的时候还没开始考虑,但是没有关系,不会对理解下面的内容产生影响)
忽略记忆材料的差异是说,测量可提取性时,统计除了记忆材料外其他属性都相同的数据。虽然无法对一位学习者、一条材料进行多次独立实验,但一位学习者、多条材料就可以了。而忽略学习者的差异,则是对多位学习者、一条材料进行统计。
考虑到 MaiMemo 的数据量较为充分,本节仅介绍忽略学习者差异的测量方式。忽略后,我们便能聚合得到新的记忆行为事件组:
e_{i} :=(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , p_i, N)
其中,N 为记忆该材料且历史行为相同的学习者数量,可提取性 p=\frac{n_{r=1}}{N} 是这些学习者中回忆成功的比例。当 N 足够大时,比率 n_{r=1}/N 接近真实的可提取性。
解决了可提取性之后,稳定性也就迎刃而解了。测量稳定性的方法是遗忘曲线,根据收集的数据,可以使用指数函数来回归计算 (item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}}) 相同的记忆行为事件组的稳定性。
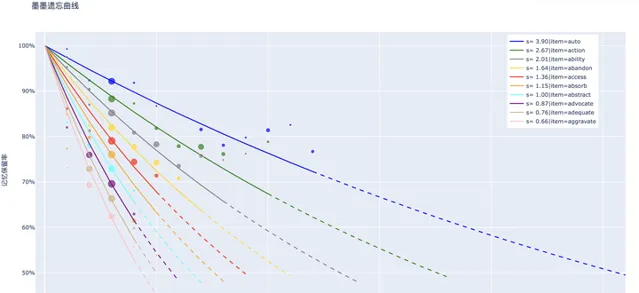
图中的散点坐标为 (\Delta t_i , p_i) ,相对大小为 \log N 。曲线是拟合后的遗忘曲线。
最后,该对难度下手了。如何从记忆数据中得出难度?让我们先从一个简单的思想实验开始。假设有一群学习者,第一次记忆 apple 和 accelerate 两个单词。如何用记忆行为数据来区分两个单词的难度?
最简单的方法,在第二天立即测试,记录记忆行为数据,统计一下,看见哪一个单词的回忆比例更高。从这一个立足点出发,我们可以将第二天的回忆比例,换成第一次记忆后的稳定性。
也就是说,第一次记忆后的稳定性能够反映出难度。但如何使用第一次记忆后的稳定性来划分难度,并没有统一的标准。怎样的划分方式最好,也没有定论。作为入门材料,本文就不详细讨论了。
状态转移
至此,我们已经可以将记忆数据转化为记忆状态:
(item, \boldsymbol{\Delta t_{1:i-1}}, \boldsymbol{r_{1:i-1}} , \Delta t_i , p_i, N) => (D_i, S_i, R_i)
接下来,我们便可以着手描述状态之间的转移关系。如 (D_i, S_i, R_i) 在 \Delta t 天后复习,回忆结果为 r ,得到新的记忆状态 (D_{i+1}, S_{i+1}, R_{i+1}) 。那么,(D_{i+1}, S_{i+1}, R_{i+1}) 与(D_i, S_i, R_i) 和 \Delta t 、r 之间的关系是什么?
首先,依然是先将记忆状态数据整理成适合分析的形式:
(D_i, S_i, R_i, \Delta t, r, D_{i+1}, S_{i+1}, R_{i+1})
其中, R_{i+1} 在复习后会立刻达到 100%,因此在分析过程中可以将其忽略。还有R_i 、\Delta t 和 S_i 之间知二求一,可以忽略掉 \Delta t 。
最终,我们要分析的状态转移数据如下:
(D_i, S_i, R_i, r, D_{i+1}, S_{i+1})
而 \cfrac{S_{i+1}}{S_i}=SInc ,正好可以参考我们在记忆稳定性增长一章中的提到的几个规律:
SInc = a S^{-b}
SInc = c e^{-d R}
可以得到关系公式(难度 D 的影响在此处被省略了):
S_{i+1} = S_{i} \cdot a S_{i}^{-b} e^{-c R_i}\textrm{(if r = 1)}
根据上式,我们预测学习者的每次回忆成功后的记忆状态 (D_{i+1}, S_{i+1}) 。反馈遗忘也是同理,可以用另一组公式状态转移方程进行描述。
SRS 模拟
有了记忆的 DSR 模型,我们便可以模拟任何复习规划下的记忆情况。那么,具体该如何模拟呢?我们需要从现实中普通人是如何使用间隔重复软件的角度出发。
假如小叶需要为四个月后的考研英语做好准备,需要使用间隔重复记忆考研考纲英语单词。而由于其他科目也需要抽时间准备。
从上面这句话中,有两个很明显的约束:学习周期天数和每日学习时间。SRS(Spaced Repetition System)模拟器需要将这两个约束考虑进来,同时这也点明了 SRS 模拟的两个维度:日间(by day)和日内(in day)。此外,考纲单词的数量是有限的,所以 SRS 模拟还有一个有限的卡片集合,学习者每天都从这个集合中挑选材料进行学习和复习。而复习任务的安排则由间隔重复调度算法来安排。整理一下,SRS 模拟需要:
- 材料集合
- 学习者
- 调度器
- 模拟时长(日内+日间)
其中学习者可以用 DSR 模型进行模拟,给出每次复习的反馈和记忆状态。调度器可以是 SM-2、Leitner box、递增间隔表,或者其他任何安排复习间隔的算法。而模拟时长和材料集合则需要根据想要模拟的情况来设定。
然后,我们从 SRS 模拟的两个维度出发,设计一下具体的模拟流程。显然,我们需要按照时间顺序,一天一天地往未来模拟,而每一天的模拟则由一张张卡片的反馈组成。所以,SRS 模拟可以由两个循环组成:外层循环表示当前模拟的日期,内层循环表示当前模拟的卡片。在内层循环中,我们需要规定每次复习所花费的时间,当累计时间超过每日学习时长限制时,自动跳出循环,准备进入下一天。
SRS 模拟的伪代码如下:
 相关的 Python 代码我开源在了 GitHub 上,感兴趣的读者可以自行阅读代码:L-M-Sherlock/space_repetition_simulators: 间隔重复模拟器 (github.com)
相关的 Python 代码我开源在了 GitHub 上,感兴趣的读者可以自行阅读代码:L-M-Sherlock/space_repetition_simulators: 间隔重复模拟器 (github.com)
SSP-MMC 算法
说完了 DSR 模型和 SRS 模拟,我们已经能够预测学习者的记忆状态和在给定复习规划下的记忆情况,但是仍然没有回答我们的最终问题:怎样的复习规划是最高效的?如何找到最优的复习规划呢?SSP-MMC 算法从最优控制的角度解决了这一问题。
SSP-MMC 是 Stochastic Shortest Path 和 Minimize Memorization Cost 的缩写,以体现这一算法的数学工具和优化目标。以下内容改编自我的毕业论文【基于 LSTM 和间隔重复模型的复习调度算法研究】 [1] 和会议论文 A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling [2] 。
问题场景
间隔重复方法的目标在于帮助学习者高效地形成长期记忆。而记忆稳定性反映了长期记忆的存储强度,复习次数、每次复习所花费的时间则反映了记忆的成本。所以,间隔重复调度优化的目标可以表述为:在给定记忆成本约束内, 尽可能让更多的材料达到目标稳定性,或以最小的记忆成本让一定量的记忆材料达到目标稳定性。其中,后者的问题可以简化为如何以最小的记忆成本让一条记忆材料达到目标稳定性,即最小化记忆成本(Minimize Memorization Cost, MMC)。
DSR 模型满足马尔可夫性,每次记忆的状态只取决于上一次的记忆状态和当前的复习输入和结果。其中回忆结果服从一个与复习间隔有关的随机分布。由于记忆状态转移存在随机性,一条记忆材料达到目标稳定性所需的复习次数是不确定的。因此,间隔重复调度问题可以视作一个 无限阶段的随机动态规划问题。考虑优化目标是让记忆稳定性达到目标水平,所 以本问题存在终止状态,可以转化为一个随机最短路径问题(Stochastic Shortest Path, SSP)。
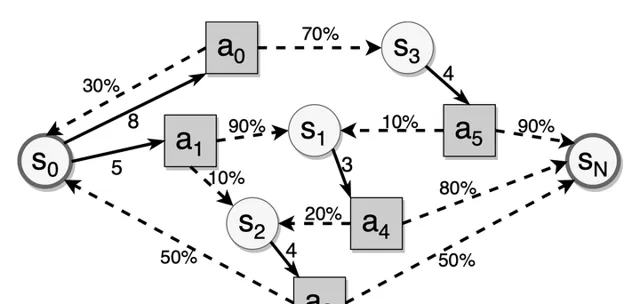
如上图所示,圆圈是记忆状态,方块是复习行为(即当前复习后的间隔),虚线箭头表示给定复习间隔的状态转移,黑边表示给定记忆状态中可用的复习间隔。间隔重复中的随机最短路径问题是找到最佳复习间隔,以最小化到达目标状态的预期复习成本。
方法表述
为了解决这个问题,可以用马尔科夫决策过程(MDP)来建模每张卡片的复习过程,有一组状态 \mathcal{S} 、行为 \mathcal{A} 、状态转换概率 \mathcal{P} 和成本函数 \mathcal{J} 。算法的目标是找到一个策略 \pi ,使达到目标状态 s_N 的预期复习成本最小。
\pi^{*}=\underset{\pi \in \Pi}{\operatorname{argmin}} \lim\limits_{N\to \infty} E_{s_{0}, a_{0}, \ldots}\left[\sum_{t=0}^{N} \mathcal{J}\left(s_{t}, a_{t}\right) \mid \pi\right]
状态空间 S 取决于记忆模型的状态大小。DSR 只有两个状态变量,所以状态可以表述为 s=(D,S) 。行为空间 \mathcal{A}=\{\Delta t_1,\Delta t_2,\cdots,\Delta t_n\} 由可以安排复习的 N 个间隔组成。状态转换概率 \mathcal{P}_{s,a}(s') 是卡片在状态 s 和行为 a 下被回忆的概率。成本函数 \mathcal{J} 定义为:
\begin{aligned} \mathcal{J}(s_0) & = \lim\limits_{N\to \infty} E\left[\sum\limits_{t=0}^{N-1}g_t(s_t,a_t(s_t), r_t) \right]\\ r_{t} & \sim Bernoulli(p_{t}) \end{aligned}
其中 g_t 是每次复习的成本, r_t 是服从伯努利分布的回忆结果。目标状态 s_N 即目标稳定性所对应的状态。
算法设计
可以用值迭代方法来解决 \textrm{MDP}(\mathcal{S},\mathcal{A},\mathcal{P},\mathcal{J}) ,其贝尔曼方程为:
\begin{aligned} \mathcal{J}^*(s) & = \min\limits_{a \in \mathcal{A}(s)} \left[\sum\limits_{s'}\mathcal{P}_{s,a}(s')(g(r) + \mathcal{J}^*(s'))\right]\\ s' & = \mathcal{F}(s,a,r,p) \end{aligned}
其中 \mathcal{J}^* 是最优成本函数, \mathcal{F} 是状态转移函数,即 DSR 模型。对于每次复习的成本,出于简单起见,只考虑回忆结果的影响: g(r) = a \cdot r + b \cdot (1-r) ,a 是回忆成功的成本,b 是回忆失败的成本。
基于该贝尔曼方程,下图所示的值迭代算法在迭代过程中使用成本矩阵来记录最优成本,使用策略矩阵来保存每个状态的最佳行为。

不断遍历每个记忆状态下的每个可选的复习间隔,比较选择当前复习间隔后的期望记忆成本和成本矩阵中的记忆成本,如果当前复习间隔的成本更低,就更新对应的成本矩阵和策略矩阵,最终所有记忆状态对应的最优间隔和成本就会收敛。
这样以来,我们便得到了最优复习策略,与预测记忆状态的 DSR 模型相结合,便可为每一位使用 SSP-MMC 记忆算法的学习者安排最高效的复习规划。
更多相关研究资源,请见:
参考
- ^ [本科毕设] 基于 LSTM 和间隔重复模型的复习算法研究 https://zhuanlan.zhihu.com/p/626308184
- ^ KDD'22 | 墨墨背单词:基于时序模型与最优控制的记忆算法 [AI+教育] https://zhuanlan.zhihu.com/p/577383961





