消费者最优化互推关系:
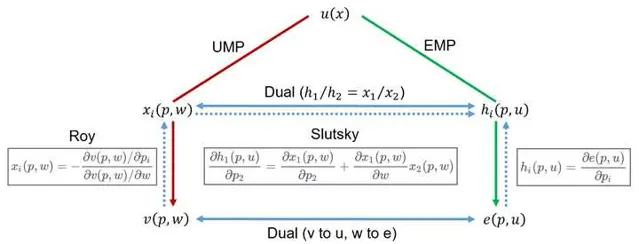
消费者的两种最优化问题均和效用函数、预算约束有关:
① 左内侧: 效用最大化问题 (UMP)
\display style \max_{ x_1,x_2} \ u(x_1,x_2)\ \ {\rm s.t.}\ \ p_1 · x_1+p_2·x_2 ≤ w拉格朗日函数为:
\mathcal L = u(x_1,x_2)-\lambda( p_1 · x_1+p_2·x_2 - w)分别对 x_1,x_2 求得两个一阶条件,做比消去 \lambda 得到 x_1,x_2 的关系式。
然后代入预算约束得 瓦尔拉斯需求函数 x_i(p,w) :
然后将所得表达式代回 u(x_1,x_2) ,消去 x_1,x_2 得到 间接效用函数 v(p,w) 。
② 右内侧: 支出最小化问题 (EMP)
\display style \min_{x_1,x_2} \ p_1 · x_1+p_2·x_2 \ \ {\rm s.t.}\ \ u( x_1,x_2) ≥ u拉格朗日函数为:
\mathcal L = p_1 · x_1+p_2·x_2-\lambda( u( x_1,x_2)- u)分别对 x_1,x_2 求到两个一阶条件,做比消去 \lambda 得到 x_1,x_2 的关系式。
然后代入效用函数得 希克斯需求函数 (补偿需求函数) h_i(p,u) :
然后将所得表达式代入下式(将 w 符号替换为 e ),得到 支出函数 :
e(p, u) = p_1h_1+ p_2h_2③ 左外侧: 罗伊恒等式 (Roy's identity),用间接效用函数反推瓦尔拉斯需求函数:
\boxed{\display style x_i(p,w) = - \frac{\partial v(p,w)/\partial p_i}{\partial v(p,w)/\partial w}}④ 右外侧:支出函数对价格求偏导,反推希克斯需求函数的公式
\boxed{\display style h_i(p, u) = \frac{∂e(p, u)}{∂p_i}}⑤ 上方: 斯勒茨基方程 (Slutsky equation),描述斯勒茨基分解
\boxed{\display style \frac{∂h_1(p, u)}{\partial p_2} = \frac{∂x_1( p, w)}{\partial p_2}+\frac{∂x_1(p, w)}{\partial w} x_2(p, w)}⑥ 下方: 对偶性 , v 换 u , w 换 e
例 :道格拉斯效用函数 u(x_1, x_2) = x^α_1 x^{1−α} _2 的间接效用函数为:(推导见例4)
v(p,w) = α^α(1 − α)^{1−α}p^{ −α}_ 1 p^{α−1}_ 2 w与这个效用函数相关的支出函数是:
e(p, u) = (α^{ −α}(1 − α)^{α−1})p^α_1 p^{1−α}_ 2 u










