太數學的東西就不說了,只用通俗唱法回答樓主的問題。
蒙特卡羅演算法並不是一種演算法的名稱,而是對一類隨機演算法的特性的概括。媒體說「蒙特卡羅演算法打敗武宮正樹」,這個說法就好比說「我被一只脊椎動物咬了」,是比較火星的。實際上是ZEN的演算法具有蒙特卡羅特性,或者說它的演算法屬於一種蒙特卡羅演算法。
那麽「蒙特卡羅」是一種什麽特性呢?我們知道,既然是隨機演算法,在采樣不全時,通常不能保證找到最優解,只能說是盡量找。那麽根據怎麽個「盡量」法兒,我們我們把隨機演算法分成兩類:
舉個例子,假如筐裏有100個蘋果,讓我每次閉眼拿1個,挑出最大的。於是我隨機拿1個,再隨機拿1個跟它比,留下大的,再隨機拿1個……我每拿一次,留下的蘋果都至少不比上次的小。拿的次數越多,挑出的蘋果就越大,但我除非拿100次,否則無法肯定挑出了最大的。這個挑蘋果的演算法,就屬於蒙特卡羅演算法—— 盡量找好的,但不保證是最好的 。
而拉斯維加斯演算法,則是另一種情況。假如有一把鎖,給我100把鑰匙,只有1把是對的。於是我每次隨機拿1把鑰匙去試,打不開就再換1把。我試的次數越多,開啟(最優解)的機會就越大,但在開啟之前,那些錯的鑰匙都是沒有用的。這個試鑰匙的演算法,就是拉斯維加斯的—— 盡量找最好的,但不保證能找到 。
所以你看,這兩個詞並不深奧,它只是概括了隨機演算法的特性,演算法本身可能復雜,也可能簡單。這兩個詞本身是兩座著名賭城,因為賭博中體現了許多隨機演算法,所以借過來命名。
這兩類隨機演算法之間的選擇,往往受到問題的局限。如果問題要求在有限采樣內,必須給出一個解,但不要求是最優解,那就要用蒙特卡羅演算法。反之,如果問題要求必須給出最優解,但對采樣沒有限制,那就要用拉斯維加斯演算法。對於機器圍棋程式而言,因為每一步棋的運算時間、堆疊空間都是有限的,而且不要求最優解,所以ZEN涉及的隨機演算法,肯定是蒙特卡羅式的。
機器下棋的演算法本質都是搜尋樹,圍棋難在它的樹寬可以達到好幾百(國際象棋只有幾十)。在有限時間內要遍歷這麽寬的樹,就只能犧牲深度(俗稱「往後看幾步」),但圍棋又是依賴遠見的遊戲,甚至不僅是看「幾步」的問題。所以,要想保證搜尋深度,就只能放棄遍歷,改為隨機采樣——這就是為什麽在沒有MCTS(蒙特卡羅搜樹)類的方法之前,機器圍棋的水平幾乎是笑話。而采用了MCTS方法後,搜尋深度就大大增加了。比如,在題主說的ZEN與武宮正樹九段的對局中,我們可以看這一步棋:
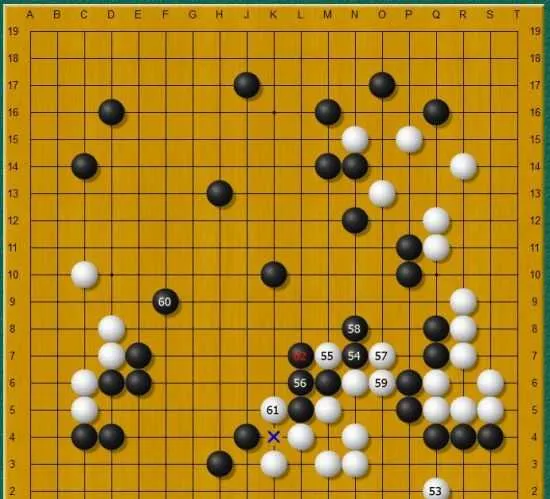
武宮正樹九段(執白)第53步大飛,明顯企圖攻角,而ZEN(執黑)卻直接不理,放棄整個右下角,轉而把中腹走厚。這個交換究竟是否劃算,就不在這裏討論了,但我們至少可以看出,ZEN敢於在此脫先,舍棄這麽大的眼前利益,其搜尋深度確實達到了人類專業棋手的水平。










