先上一個圖
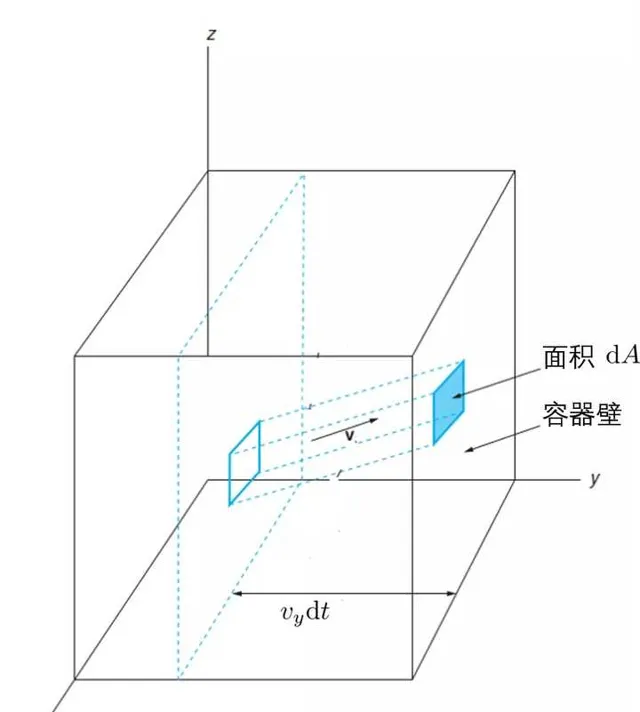
單位時間撞擊到面積元 \mathrm dA 的速度為 \vec{v} 的分子都在圖中的柱體內,數目為
\mathrm dN'(v_y)= nv_yf(v_y)\mathrm dv_y\mathrm dt\mathrm dA
其中 f(v_y) 為分子的速度分布。
各種速度的分子都考慮進去,
\begin{split} N'=&\int \mathrm dN'(v_y)\\\\ =&n\mathrm dt\mathrm dA \int_0^{\infty}v_yf(v_y)\mathrm dv_y \\\\ =&n\mathrm dt\mathrm dA\int_{0}^{\infty} \left(\frac{m}{2\pi kT}\right)^{1/2}\exp\left(-\frac{mv_y^2}{2 kT}\right)v_y\mathrm dv_y \\\\ =&n\mathrm dt\mathrm dA \left(\frac{kT}{2\pi m}\right)^{1/2} =\frac{n}{4}\left(\frac{8kT}{\pi m}\right)^{1/2}\mathrm dt\mathrm dA \\\\ =&\frac{n\bar{v}}{4}\mathrm dt\mathrm dA \end{split}
單位時間碰撞到器壁單位面積上的分子數為:
\Gamma=\frac{N'}{\mathrm dt\mathrm dA }=\frac{n\bar{v}}{4}
@qfzklm 大佬說了,不需要麥克斯韋分布,只要速率分布球對稱即可。
用極座標再處理一下上面的問題。
先上圖
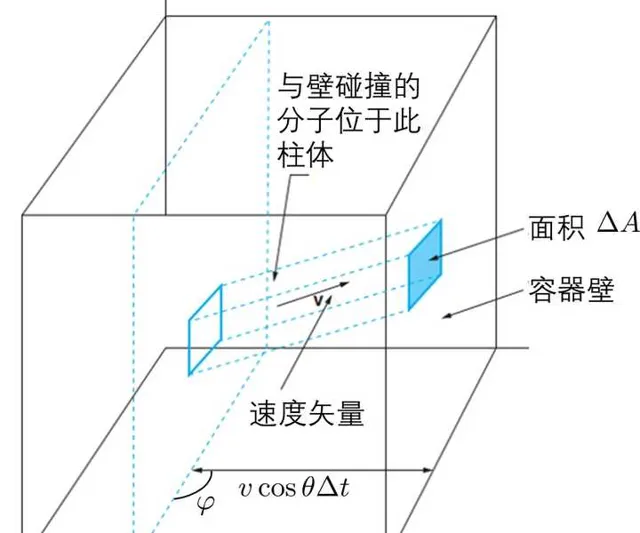
現在開始用極座標計算
\begin{split} N'=& n\mathrm dt\mathrm dA \cdot \frac{1}{4\pi} \int_0^{\infty}\int_0^{\pi/2}v\cos\theta f(v)\mathrm dv \sin\theta \mathrm d\theta\int_0^{2\pi}\mathrm d\varphi \\\\ =& \frac{n\mathrm dt\mathrm dA}{4\pi} \int_0^{\infty}v f(v)\mathrm dv \int_0^{\pi/2} \cos\theta \sin\theta \mathrm d\theta\int_0^{2\pi}\mathrm d\varphi \\\\ =& \frac{n\mathrm dt\mathrm dA}{4\pi} \int_0^{\infty}v f(v) \mathrm dv \cdot \frac{1}{2}\cdot (2 \pi) \\\\ =& \frac{nv_{\mathrm a}}{4}\mathrm dt\mathrm dA \end{split}
單位時間碰撞到器壁單位面積上的分子數為:
\Gamma=\frac{N'}{\mathrm dt\mathrm dA }=\frac{n\bar{v}}{4}
大佬的洞察是對的,不需要速度分布是麥克斯韋分布,只需要速度分布是球對稱即可。











